J'ai rencontré une question de test écrite et je n'en avais aucune idée. Veuillez demander de l'aide. . . .
Les classes connues sont définies comme suit
class Node {
public Double value;
public List<Node> children;
}Le nœud d'entrée satisfait aux conditions suivantes :
1 La valeur du nœud est un nombre à virgule flottante supérieur à 0
2 La valeur des nœuds subordonnés du nœud (et des nœuds de niveau inférieur) peut être nulle ou un nombre à virgule flottante supérieur à 0
La fonction du programme est la suivante :
1 sera Toutes les valeurs nulles de la structure arborescente sont définies sur des nombres à virgule flottante supérieurs à 0
2 La valeur d'un nœud non-feuille (c'est-à-dire un nœud avec. un nombre d'enfants supérieur à 0) est égal à la somme des valeurs de ses enfants
public void doit(Node node){
......
}Exemple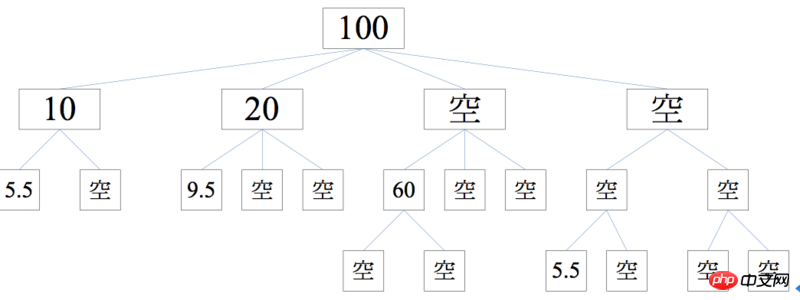
Réponse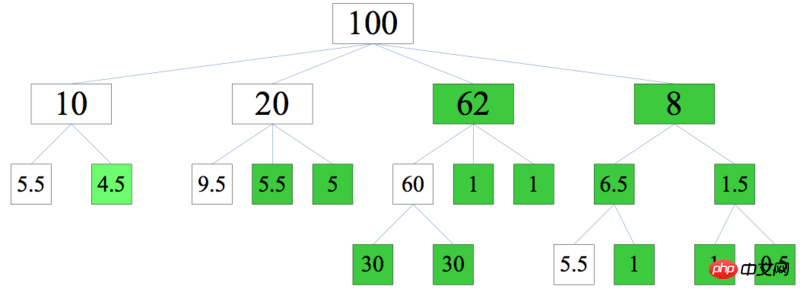
Comment répondre à cette question ?
Certains experts y ont déjà répondu. Combiner les réponses des deux personnes ci-dessous est la réponse parfaite. En fait, si j'adopte la réponse et change la distribution égale en aléatoire, ce sera parfait
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
Je n'ai pas écrit de code spécifique, mais parlons de l'idée
Tout d'abord, divisez le problème en 2 étapes
Étape 1 Déterminez la valeur du nœud non-feuille
. Étape 2. Déterminez la valeur du nœud feuille#🎜 🎜# Traitez d'abord l'étape 1. Après avoir traité l'étape 1, il n'est pas nécessaire d'en dire plus sur l'étape 2. Divisez-la simplement en fonction de la valeur du nœud parent.
Pour l'étape 1,
étape1-1 : Parcourez chaque nœud non-feuille de bas en haut et déterminez sa valeur minimale en additionnant ses nœuds enfants. Par exemple, le sous-arbre le plus à droite a une valeur minimale de 5,5.
étape 1-2 : De haut en bas, déterminez les nœuds non-feuilles couche par couche, qui sont des descriptions d'aspect Nom [100] comme première couche, [10, 20, ?, ?] comme deuxième couche. , et ainsi de suite. . Selon le résultat de l'étape 1-1, la valeur minimale de la deuxième couche est [10, 20, >60, >5,5]. Soustrayez la somme des valeurs minimales de 100, puis divisez-la également. le résultat est [10, 20, 62.25, 7.75]
step1-3 : Comme ci-dessus, déterminez la troisième couche, le résultat est [5.5, 4.5] [9.5, 5.25, 5.25] [60, 1.125, 1.125] [6.625, 1.125]
Le dernier ici Le groupe est spécial Il faut considérer que lorsque 7.75 est attribué, il y a déjà 5.5 en bas à gauche, donc le nombre à votre disposition en 7.75 est 7.75-5.5= 2,25. Divisez 2,25 de manière égale des deux côtés, et le résultat est [6,625, 1,125]#🎜🎜 #étape 1-4 : Je pense que la dernière couche n'a pas besoin d'être détaillée, c'est en fait l'étape 2, divisez-la simplement de manière égale.
Je viens de lire cette question et je l'ai trouvée très intéressante. Ensuite, j'y ai réfléchi et j'ai posé les questions suivantes.
Mon idée est la récursivité.
Parcourez hiérarchiquement, additionnez les valeurs déterminées à chaque niveau et divisez les nœuds vides par la valeur du nœud parent moins la somme des valeurs déterminées (exigences de la question). Ensuite, si le nœud n'est pas un nœud feuille, récurez selon la méthode ci-dessus.
Mais lors de la détermination de la valeur de chaque nœud, comme certains nœuds feuilles, nous devons leur attribuer des valeurs de manière aléatoire. Certaines de leurs valeurs sont contraintes par le nœud parent, et d'autres ne sont pas contraintes par le nœud parent. , comme le troisième nœud de la deuxième couche. Les deux nœuds feuilles de , si les valeurs que nous leur attribuons font que leurs nœuds parents ne répondent pas aux exigences, cela ne répond pas au sens de la question. Donc ce que je veux, c'est passer dans la plage de valeurs de ces nœuds à chaque fois que la valeur est déterminée. La détermination de ces domaines entraînera certains problèmes, et les problèmes deviendront compliqués.
La plage est déterminée. La valeur maximale de chaque nœud vide doit être la somme de la valeur du nœud parent moins la valeur du même nœud enfant. La valeur minimale doit être supérieure à la somme des éléments précieux de ses nœuds enfants. . Étant donné que seule une certaine plage est déterminée, la sélection de certaines valeurs aléatoires de ses nœuds feuilles n'empêchera pas les nœuds restants de répondre au sens de la question. De manière générale, les valeurs de chaque nœud vide avec le même nœud parent sont mutuellement contraintes. Bien que la valeur d'un nœud se satisfasse, les autres nœuds ne répondront pas aux exigences. Par exemple :
Si la valeur est prise de cette manière, elle sera satisfaite localement, ce qui empêchera les valeurs des autres nœuds de répondre aux exigences. Cela peut donc conduire à des résultats inattendus sans contraintes. Nous devons déterminer ces plages.
Pour résumer, ce ne sont que quelques-unes de mes réflexions après y avoir réfléchi. Il peut y avoir des erreurs et corrigez-moi s'il vous plaît.