Le dernier théorème de Fermat est sur le point d’être conquis par l’IA ?
Et la partie la plus significative de tout cela est que le dernier théorème de Fermat que l’IA est sur le point de résoudre vise précisément à prouver que l’IA est inutile.
Autrefois, les mathématiques appartenaient au domaine de l'intelligence humaine pure ; aujourd'hui, ce territoire est déchiffré et piétiné par des algorithmes avancés.
Photos
Le dernier théorème de Fermat est un casse-tête « notoire » qui intrigue les mathématiciens depuis des siècles.
Cela a été prouvé en 1993, et maintenant, les mathématiciens ont un grand plan : utiliser des ordinateurs pour reproduire le processus de preuve.
Ils espèrent que dans cette version de la preuve, s'il y a des erreurs logiques, elles pourront être vérifiées par un ordinateur.
Adresse du projet : https://github.com/riccardobrasca/flt3
Fin mars, le mathématicien Pietro Monticone a déclaré avec enthousiasme que lui et ses collègues avaient presque terminé Fermat avec l'exposant 3 dans la formalisation du leanprover du dernier théorème.
Ils porteront le processus formel sur Mathlib dès que possible pour une utilisation dans le projet FLT.
Photos
Le processus de preuve suit à peu près la preuve de Wiles, mais avec de légères modifications.
Quand avril viendra, le mathématicien et programmeur Kevin Buzzard publiera ce plan : compléter la preuve du dernier théorème de Fermat via du code informatique.
Après la mise en ligne du projet en avril, le plan public apparaîtra en ligne. À ce moment-là, n'importe quel membre de la communauté Lean pourra apporter sa propre contribution à la preuve formelle.
Photos
Transformer une preuve mathématique révolutionnaire de 100 pages en code informatique Ce processus est-il facile à mettre en œuvre ?
C'est bien sûr grâce à l'outil de preuve Lean, très apprécié et accro à l'utilisation de Terence Tao, qui permet aux utilisateurs de convertir des preuves de style prose en règles et logiques pour les tests.
Photos
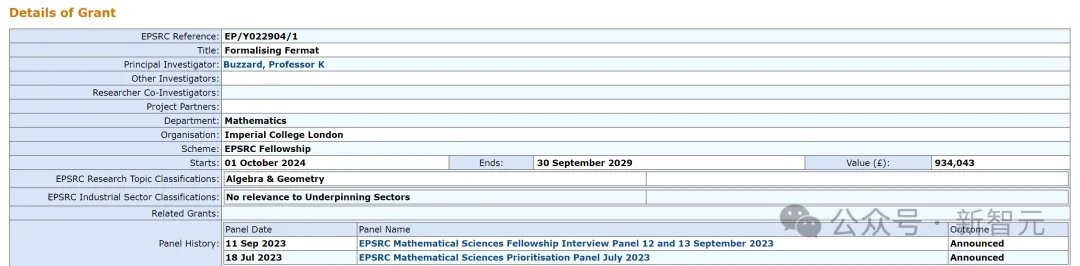
Cependant, ce projet n'est pas simple et devrait prendre de nombreuses années, et Kevin Buzzard Page a reçu un soutien financier pour le projet.
Photos
Tout le monde comprend que ce projet est probablement l'une des démonstrations informatisées les plus complexes à ce jour.
Photos
Le dernier théorème de Fermat est le puzzle mathématique le plus excitant de l'histoire.
Le processus de preuve du dernier théorème de Fermat est directement une histoire des mathématiques.
Images
Le fameux dernier théorème de Fermat a été proposé par le mathématicien français du XVIIe siècle Pierre de Fermat. Malheureusement, il n’a pas pu en trouver la preuve de son vivant.
Ainsi, ce problème né il y a plus de 300 ans a directement défié l’humanité pendant trois siècles, choqué le monde à plusieurs reprises, épuisé l’énergie de nombreux cerveaux parmi les plus remarquables de l’humanité et fasciné des milliers d’amateurs.
Image
Ce théorème affirme qu'il n'y a pas trois entiers positifs a, b, c qui satisfont à l'équation (a^n + b^n = c^n), où n est un entier supérieur à 2 .
La difficulté de cette preuve est qu'il est difficile pour les mathématiciens de trouver un cas négatif : Comment pouvons-nous garantir qu'il n'existe pas d'entier infini n qui puisse satisfaire cette équation ?
Photos
Heureusement, pour les mathématiciens d’aujourd’hui, convertir le concept d’infini en logique n’a rien de nouveau.
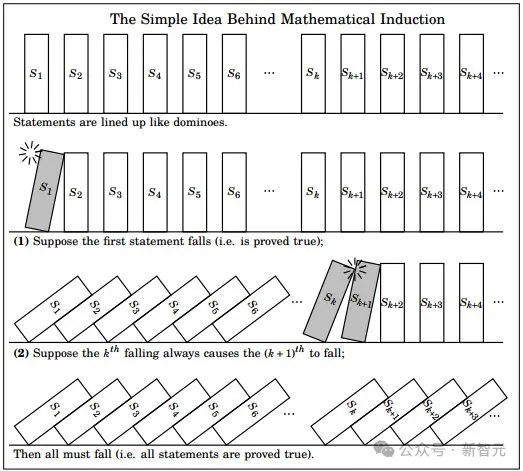
Dans la preuve la plus simple, nous pouvons compter sur l'induction -
Une fois qu'une certaine logique est vraie pour un certain nombre (comme 8), alors elle sera vraie pour chaque nombre suivant (comme 9, 10 , 11, etc.) sont également vrais jusqu’à l’infini.
Photos
Cependant, le dernier théorème de Fermat est une pierre d'achoppement dans le monde mathématique depuis des centaines d'années.
Ce n'est qu'en 1993 que le mathématicien britannique Andrew Wiles a résolu ce mystère avec une preuve écrite de 100 pages.
Photos
Pourquoi les ordinateurs ne peuvent-ils pas prouver le dernier théorème de Fermat ?
L'industrie estime qu'il y a trois raisons :
1. Les ordinateurs ne peuvent pas déduire des espèces infinies
2. Les ordinateurs ne peuvent pas prouver que la logique est correcte
3. peut apparaissent des erreurs passagères
Heureusement, il existe une preuve auxiliaire LeanHeureusement, nous ne pouvons plus nous appuyer sur les méthodes de preuve traditionnelles et pouvons nous tourner vers des outils comme le Lean.
C'est un outil de programmation développé basé sur C++, spécialement conçu pour écrire et vérifier des preuves d'induction.
Beaucoup des soi-disant « intelligences artificielles » d’aujourd’hui ne sont rien de plus que des mots intelligemment disposés qui imitent le langage humain. Mais les épreuves assistées par ordinateur telles que Lean intègrent plus profondément la pensée humaine et les capacités améliorées assistées par ordinateur.
Photos
Grâce à ces outils, les élèves peuvent décomposer le contenu discuté en classe en étapes d'opérations logiques et mathématiques.
C'est comme la pierre de Rosette des preuves mathématiques.
Clarissa Littler, qui est également professeur de mathématiques, est tout à fait d'accord avec la philosophie de Kevin Buzzard.
Elle enseigne les mathématiques discrètes au Portland Community College. Au cours des deux derniers semestres, elle a utilisé le « Lean Classic Introductory Game » développé par Kevin Buzzard dans son cours de mathématiques discrètes.
Photos
Elle utilisera le "Natural Number Game" pour aider les élèves à se familiariser avec l'idée de l'induction mathématique, et grâce au "Set Theory Game", elle les habituera à raisonner sur les ensembles. Dans ce processus, l'écart de compréhension des élèves entre « suivre strictement des règles logiques pour rédiger des preuves » et « utiliser un langage populaire pour expliquer la vérité des choses » sera progressivement comblé. Littler a souligné que l'un des objectifs majeurs du cours est de permettre aux étudiants ayant de faibles bases en mathématiques de penser plus librement à la manière des mathématiciens, tout en comprenant mieux les preuves, les preuves et les méthodes de démonstration de la vérité. Ce passage de la logique formelle aux listes de règles et à l'expression en prose est essentiel pour décomposer les projets en morceaux de code coopérants. Ceci est particulièrement important à l'intersection de la programmation et des mathématiques pures, et c'est là que des outils comme Lean peuvent briller. Buzzard a déclaré qu'il espérait transformer les idées mathématiques complexes déclenchées par le dernier théorème de Fermat en une forme programmable. Au fil des siècles, de nombreuses nouvelles branches précieuses des mathématiques ont été créées afin de prouver ce théorème, qui, selon Buzzard, "n'a aucune signification pratique". Oui, selon Buzzard, le dernier théorème de Fermat n’a aucun sens et n’a aucune application dans le monde réel. Cependant, à cause de ce problème « notoire », de nombreuses nouvelles idées brillantes ont été produites ces dernières années. Maintenant, la conversion de la preuve de 100 pages de Wiles en un langage formel et des règles que les ordinateurs peuvent comprendre devrait ouvrir la porte à des preuves assistées par ordinateur pour une nouvelle génération de mathématiciens. Et cet outil de conversion peut également aider les programmeurs. Littler a déclaré que dans ce domaine, les projets ambitieux valent toujours la peine d'être essayés car nous pouvons tous bénéficier des leçons apprises et des bibliothèques écrites. Bien que la démonstration interactive de théorèmes soit encore un domaine relativement nouveau, la communauté Lean a fait beaucoup d'excellent travail. Kevin Mark Buzzard, né en 1968, possède de profondes connaissances professionnelles en géométrie arithmétique et en programmes Langlands. Il est actuellement professeur de mathématiques pures à l'Imperial College de Londres et « évangéliste » de l'outil d'IA Lean. Pendant ses études à la Royal Grammar School, Kevin Buzzard a participé à l'Olympiade mathématique internationale et a remporté la médaille de bronze en 1986 et la médaille d'or avec des scores parfaits en 1987. Par la suite, il a terminé ses études de premier cycle en mathématiques au Trinity College de l'Université de Cambridge, recevant le titre de Senior Wrangler en 1990 et le diplôme C.A.S.M. Sous la direction de Richard Taylor, sa thèse de doctorat « Les niveaux de représentations modulaires » a été achevée en 1995, explorant un domaine complexe des mathématiques. En 1998, il a commencé à travailler comme maître de conférences à l'Imperial College de Londres, a été promu maître de conférences en 2002 et nommé professeur en 2004. Il a également mené des recherches invitées à l'Université Harvard (d'octobre à décembre 2002) et dans plusieurs autres institutions célèbres. Pour ses contributions exceptionnelles dans le domaine de la théorie des nombres, il a remporté le Whitehead Award en 2002 et le Senior Berwick Award en 2008. En 2017, Buzzard a lancé un projet et un blog sur Lean Theorem Prover, dédié à la promotion de l'utilisation d'outils de preuve assistée par ordinateur dans la recherche mathématique. Il a également guidé le musicien Dan Snaith (nom de scène Caribou) pour terminer sa thèse de doctorat en mathématiques sur l'étude des symboles super-convergents du module Siegel, pour laquelle Snaith a obtenu son doctorat à l'Imperial College de Londres. En octobre 2023, Kevin Buzzard a déclaré sur les réseaux sociaux qu'il avait reçu un financement pour la recherche et qu'il avait commencé à utiliser Lean pour prouver le dernier théorème de Fermat. Buzzard a déclaré : "Il y a dix ans, cela aurait pris un temps infini." Il mettra entre parenthèses ses fonctions d'enseignant pendant cinq ans pour mener à bien le projet. Vaut-il la peine de suspendre ses propres tâches ? De l'avis de son collègue Chris Williams de l'Université de Nottingham au Royaume-Uni, ce type de projet peut avoir des avantages inattendus et des impacts de grande envergure. "Je pense qu'il est peu probable qu'il formalise formellement l'intégralité de la preuve dans les cinq prochaines années, sinon ce serait incroyable. Cependant, de nombreux outils sont désormais omniprésents en théorie des nombres et en géométrie arithmétique, donc je prédis que tout futur Des progrès substantiels seront très utiles." Ce projet révèle également une valeur plus profonde. Avec l'évolution continue des outils informatiques, les frontières entre les différentes branches des mathématiques, et même entre les différentes disciplines, deviennent de plus en plus floues, ce qui a conduit à l'émergence de certaines preuves presque impossibles à vérifier. Par exemple, le mathématicien japonais Mochizuki Shinichi de l'Université de Kyoto a écrit une preuve de 500 pages qui a mis plusieurs années à être publiée parce qu'elle était très compliquée, en partie parce que les gens ne savaient pas quoi en faire. Désormais, nous constaterons peut-être que les frontières des mathématiques deviennent de plus en plus floues. Cela ne fait pas référence à la véracité ou à l'ambiguïté logique, mais à l'éventail d'idées différentes qui peuvent être incorporées dans une preuve. Lean permet aux mathématiciens de convertir leurs idées en code, ce qui facilite la compréhension par leurs pairs. Au vu des précédents enregistrés par leurs prédécesseurs, les futurs mathématiciens pourront continuer à faire progresser leurs propres recherches sur cette base. Buzzard a déclaré que la caractéristique de l'écriture mathématique en Lean est que vous pouvez laisser des résultats précisément énoncés mais non prouvés, et que d'autres peuvent les résoudre plus tard. Lean lui-même facilite un tel flux de travail. En d’autres termes, le dernier théorème de Fermat se prépare à être résolu grâce au « crowdsourcing » – surtout si le travail de codage dépasse les années de travail restantes de Buzzard. Réaliser une preuve mathématique nécessite les efforts de toute la communauté. Peut-être qu'à l'avenir, nous pourrons avoir une plateforme similaire à Genius.com pour partager et interpréter des preuves mathématiques. Références : 
Images
Photos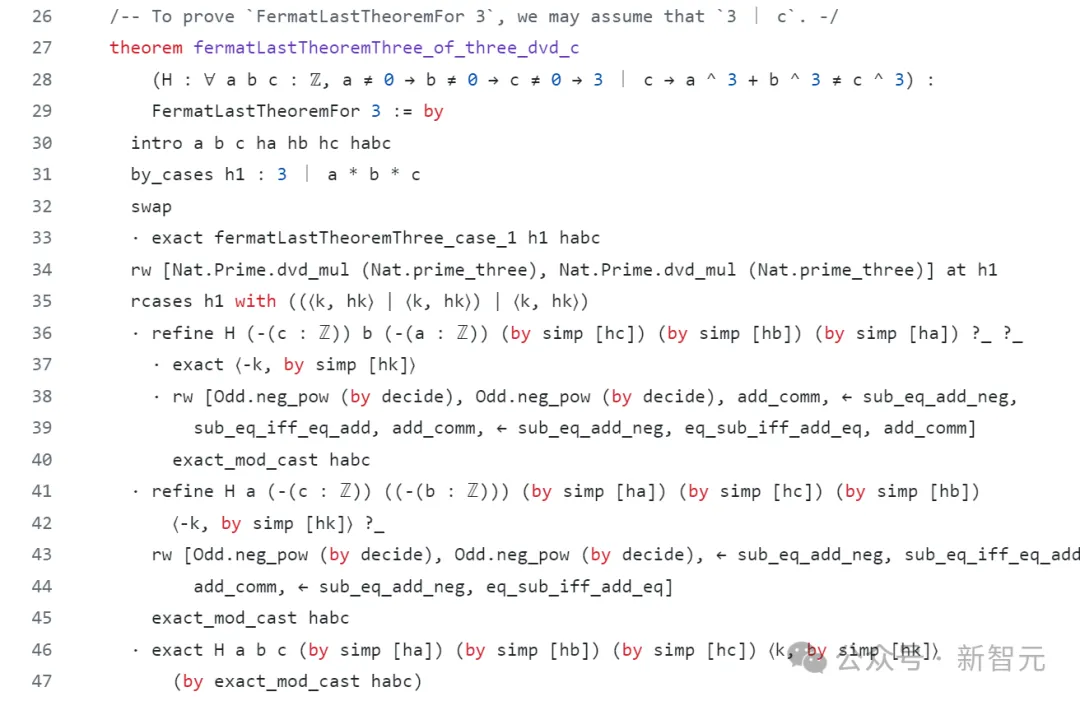
Images
Kevin Buzzard : évangéliste Lean
Photos
Photos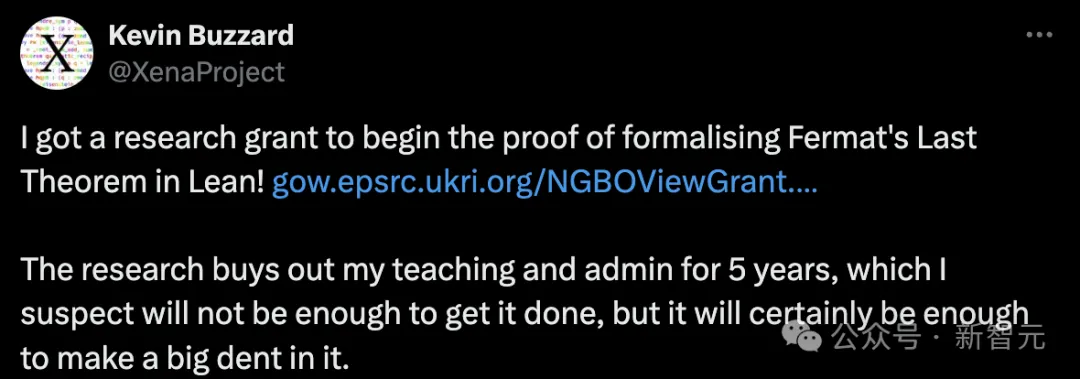
Photos
Important pour la recherche mathématique
Photos
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Construisez votre propre serveur git
La différence entre git et svn
git annuler le commit soumis
Formules de permutation et de combinaison couramment utilisées
Quelles sont les différences entre le langage C++ et C
Ordre d'apprentissage recommandé pour C++ et Python
Analyse coût-efficacité de l'apprentissage de Python et C++
Le langage C est-il identique au C++ ?
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
