Une explication simple de la fonction de densité de probabilité

Pouvez-vous expliquer brièvement ce qu'est la fonction de densité de probabilité ?

La fonction de densité de probabilité (p.d.f., fonction de densité de probabilité) décrit la distribution de probabilité de variables aléatoires et est la fonction dérivée de la fonction de distribution cumulative. [Modifier] Définition : Pour une variable aléatoire réelle unidimensionnelle $int\_\{-infty\}^\{infty\}\; f\_\; (x),dx\; =\; 1$ La probabilité d'une variable aléatoire X dans l'intervalle peut être exprimée par l'intégrale définie de son fonction de densité de probabilité : $P[a\; Et$ F(x)=P[Xest\; la\; fonction\; de\; distribution\; cumulative\; de\; X.\; Évidemment,\; la\; fonction\; de\; densité\; de\; probabilité\; est\; sa\; fonction\; dérivée.\; [Modifier]Application\; Les\; moments\; tels\; que\; la\; valeur\; attendue\; et\; la\; variation\; peuvent\; être\; obtenus\; à\; partir\; de\; la\; fonction\; de\; densité\; de\; probabilité.\; Valeur\; attendue\; (premier\; instant)\; :\; E[X]=$ int\_\{-infty\}^\{infty\}\; xf(x),dx\; Variation\; (deuxième\; instant)\; :\; VAR[X]=$ int\_\{-infty\}^\{\; infty\}\; (x-E[X])^2f(x),dx[modifier]\; La\; fonction\; caractéristique\; peut\; être\; obtenue\; par\; transformation\; de\; Fourier\; de\; la\; fonction\; de\; densité\; de\; probabilité.$ Phi\_X(jomega)\; =\; int\_\{-infty\}^\{infty\}\; f(x)e^\{jomega\; x\},dx$Il\; existe\; une\; relation\; biunivoque\; entre\; la\; fonction\; caractéristique\; et\; la\; fonction\; de\; densité\; de\; probabilité.\; Par\; conséquent,\; connaître\; la\; fonction\; caractéristique\; d’une\; distribution\; équivaut\; à\; connaître\; la\; fonction\; de\; densité\; de\; probabilité\; d’une\; distribution.\; da:Sandsynlighedst\ae thedsfunktion\; en:Fonction\; de\; densité\; de\; probabilité\; it:Funzione\; di\; densità\; di\; probabilità\; nl:Kansdichtheid\; sv:Täthetsfunktion$ $Un\; faisceau\; de\; particules\; est\; dispersé\; par\; un\; obstacle\; (situé\; en\; x\; =\; 0).\; Sa\; fonction\; d\text{'}onde\; est\; la\; suivante\; :$ .$\Psi (x,\; t)\; =\; Ae-iEt/h[quand\; x$$$$

Ψ（x, t） = e-iEt/h( Beikx+ Ce-ikx) [quand x> 0 ]

Où E = h2k2/( 2m ) et k > 0, A, B et C sont des coefficients complexes.

﹝Le « h » est « h-bar », qui est la ligne horizontale au-dessus de h﹞

(a) Calculez sa densité de probabilité p(x, t) lorsque x

(b) Calculez sa densité de flux de probabilité j(x, t) lorsque x

(c) Calculez sa densité de probabilité p(x, t) lorsque x > 0.

(d) Calculez sa densité de flux de probabilité j(x, t) lorsque x > 0.

(e) La fonction d'onde ci-dessus contient trois parties différentes, trois coefficients A, B et C. Indiquez si chacun se déplace à droite ou à gauche. Les trois représentent respectivement l’incidence, la réflexion et l’émission. Lequel est-ce ?

Remarque : les réponses à p(x, t) et j(x, t) doivent être des nombres réels.

Comment faire la distinction entre la fonction de probabilité et la densité de probabilité

Définition mathématique de la densité de probabilité

Pour la variable aléatoire X, s'il existe une fonction intégrable non négative p(x) (﹣∞

Les variables aléatoires continues sont souvent décrites intuitivement par leurs fonctions de densité de probabilité. La fonction de densité de probabilité f(x) des variables aléatoires continues a les propriétés suivantes :

Cela fait référence aux variables aléatoires continues unidimensionnelles, et les variables continues multidimensionnelles sont similaires.

Fonction de densité de probabilité des données aléatoires : représente la probabilité que l'amplitude instantanée se situe dans une plage spécifiée, et est donc fonction de l'amplitude. Cela varie en fonction de l'ampleur de la plage prise.

La fonction de densité f(x) a les propriétés suivantes :

(1)f(x)≧0;

(2) ∫f(x)d(x)=1;

(3) P(a

Supposons la fonction de densité de probabilité de la variable aléatoire X N0 1 Y |x|

Le processus de résolution de problèmes est le suivant :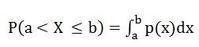

Informations détaillées

Méthode de densité de probabilité :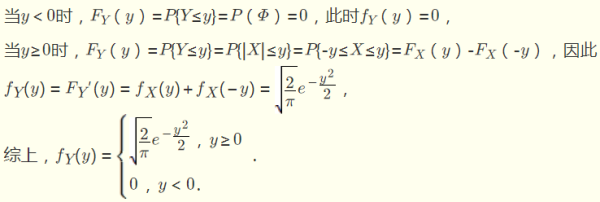

Supposons que la variable aléatoire Parmi eux, α=min(g(-∞), g(∞)), β=max(g(-∞), g(∞)), h(y) est la fonction inverse de g(x).

Parler simplement de densité de probabilité n'a aucune signification pratique. Il doit avoir comme prémisse un certain intervalle délimité. La densité de probabilité peut être considérée comme l'ordonnée et l'intervalle comme l'abscisse. L'intégrale de la densité de probabilité sur l'intervalle est la zone, et cette zone est la probabilité qu'un événement se produise dans cet intervalle. La somme de toutes les zones est 1. . Par conséquent, cela n’a aucun sens d’analyser la densité de probabilité d’un point seul. Il doit avoir un intervalle comme référence et comparaison.

La probabilité fait référence à la probabilité qu'un événement se produise de manière aléatoire. Pour une fonction de distribution uniforme, la densité de probabilité est égale à la probabilité d'un intervalle (la plage de valeurs de l'événement) divisée par la longueur de l'intervalle. négatif et peut être très grand ou très petit.

Sélectionnez un produit au hasard parmi un lot de produits authentiques et défectueux, et « celui que vous tirez est authentique » est un événement aléatoire. Supposons qu’un phénomène aléatoire soit testé et observé n fois et que l’événement A se produise m fois, c’est-à-dire que sa fréquence d’apparition est m/n. Après de nombreuses expériences répétées, m/n se rapproche souvent de plus en plus d'une certaine constante (voir la loi des grands nombres de Bernoulli pour la preuve de cette conclusion).

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!