
La régression linéaire simple est une méthode statistique utilisée pour étudier la relation entre deux variables continues. Parmi elles, une variable est appelée variable indépendante (x) et l’autre variable est appelée variable dépendante (y). Nous supposons qu'il existe une relation linéaire entre ces deux variables et essayons de trouver une fonction linéaire qui prédit avec précision la valeur de réponse (y) de la variable dépendante en fonction des caractéristiques de la variable indépendante. En traçant une ligne droite, nous pouvons obtenir les résultats prédits. Ce modèle prédictif peut être utilisé pour comprendre et prédire comment la variable dépendante change à mesure que les variables indépendantes changent.
Afin de comprendre ce concept, nous pouvons utiliser un ensemble de données salariales, qui contient la valeur de la variable dépendante (salaire) correspondant à chaque variable indépendante (années d'expérience).
Salaire annuel et expérience
1.1 39343.00
1.3 46205.00
1.5 37731.00
2.0 43525.00
2.2 91.0 0
2.9 56642.00
3.0 60150.00
3.2 54445.00
3.2 64445.00
3.7 57189.00
À des fins générales, nous définissons :
x comme vecteur de caractéristiques, soit x=[x_1,x_2,....,x_n],
y comme vecteur de réponse, soit y=[y_1,y_2, .. ..,y_n]
pour n observations (dans l'exemple ci-dessus, n=10).
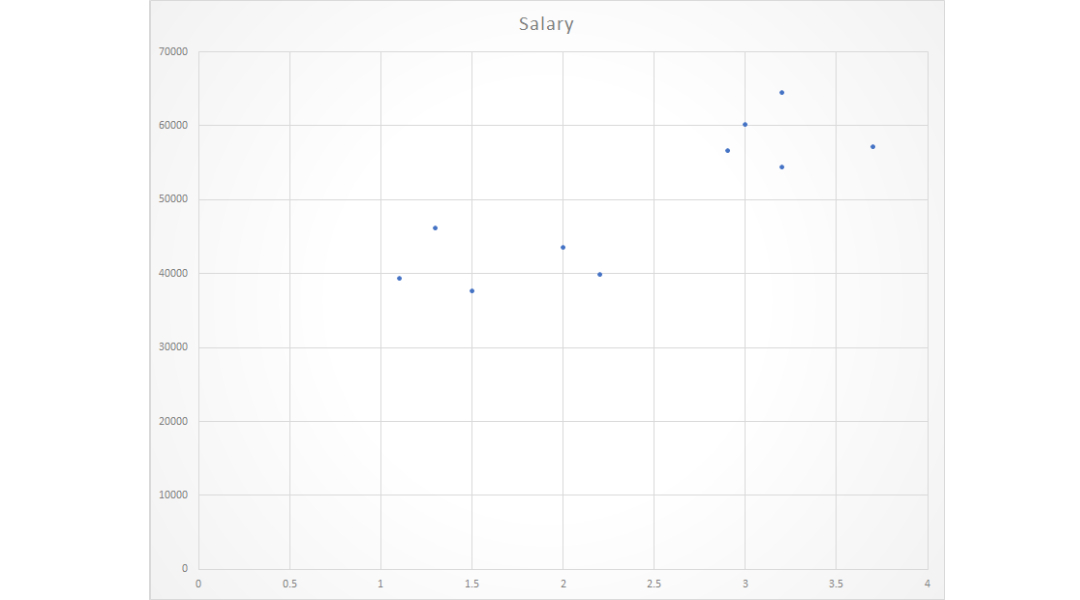
Maintenant, nous devons trouver une ligne qui correspond au nuage de points ci-dessus à travers laquelle nous pouvons prédire la réponse pour n'importe quelle valeur y ou pour n'importe quelle valeur x.
La droite de meilleur ajustement est appelée droite de régression.
dataset=read.csv('salary.csv')
install.packages('caTools')
library(caTools)
split=sample.split(dataset$Salary,SplitRatio=0.7)
trainingset=subset(dataset,split==TRUE)
testset=subset(dataset,split==FALSE)
lm.r=lm(formula=Salary~YearsExperience,
data=trainingset)
coef(lm.r)
ypred=predict(lm.r,newdata=testset)
install.packages("ggplot2")
library(ggplot2)
ggplot()+geom_point(aes(x=trainingset$YearsExperience,
y=trainingset$Salary),colour='red')+
geom_line(aes(x=trainingset$YearsExperience,
y=predict(lm.r,newdata=trainingset)),colour='blue')+
ggtitle('Salary vs Experience(Training set)')+
xlab('Years of experience')+
ylab('Salary')
ggplot()+
geom_point(aes(x=testset$YearsExperience,y=testset$Salary),
colour='red')+
geom_line(aes(x=trainingset$YearsExperience,
y=predict(lm.r,newdata=trainingset)),
colour='blue')+
ggtitle('Salary vs Experience(Test set)')+
xlab('Years of experience')+
ylab('Salary')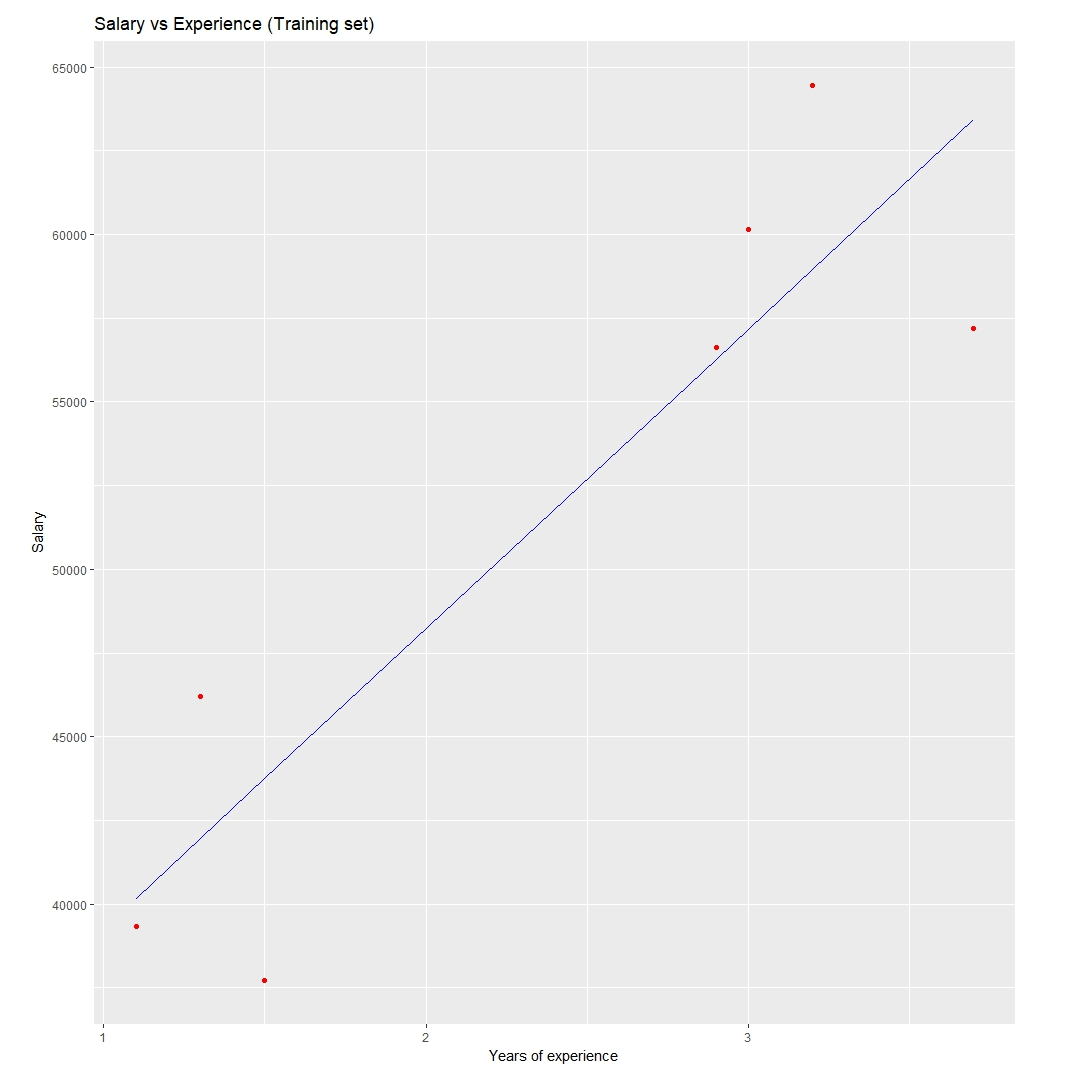
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Qu'est-ce que j2ee
Qu'est-ce que j2ee
 Quelles sont les méthodes pour se connecter au serveur vps
Quelles sont les méthodes pour se connecter au serveur vps
 Comment transformer deux pages en un seul document Word
Comment transformer deux pages en un seul document Word
 Comment créer un clone WeChat sur un téléphone mobile Huawei
Comment créer un clone WeChat sur un téléphone mobile Huawei
 Quels sont les moyens de dégager les flotteurs ?
Quels sont les moyens de dégager les flotteurs ?
 largeur de décalage
largeur de décalage
 Que dois-je faire si le disque temporaire ps est plein ?
Que dois-je faire si le disque temporaire ps est plein ?
 Tableau de mots réparti sur plusieurs pages
Tableau de mots réparti sur plusieurs pages