GPT-4 crée un « modèle mondial », permettant au LLM d'apprendre des « mauvaises questions » et d'améliorer considérablement sa capacité de raisonnement

Récemment, les grands modèles de langage ont fait des percées significatives dans diverses tâches de traitement du langage naturel, en particulier dans les problèmes mathématiques qui nécessitent un raisonnement en chaîne de pensée (CoT) complexe

Par exemple, dans GSM8K, MATH, etc. Modèles propriétaires, notamment GPT -4 et PaLM-2 ont obtenu des résultats remarquables sur des ensembles de données de tâches mathématiques difficiles. À cet égard, les grands modèles open source ont encore une marge d’amélioration considérable. Pour améliorer encore les capacités d'inférence CoT des grands modèles open source pour les tâches mathématiques, une approche courante consiste à affiner ces modèles à l'aide de paires de données d'inférence question-inférence annotées/générées (données CoT) qui enseignent directement au modèle comment effectuer des tâches sur ces derniers. Effectuez l’inférence CoT pendant la tâche.

Récemment, des chercheurs de l'Université Jiaotong de Xi'an, de Microsoft et de l'Université de Pékin ont discuté d'une idée d'amélioration dans un article, qui consiste à améliorer davantage sa capacité de raisonnement grâce au processus d'apprentissage inversé (c'est-à-dire apprendre des erreurs du LLM)

Tout comme un élève qui commence à apprendre les mathématiques, il améliorera d'abord sa compréhension en étudiant les points de connaissance et les exemples du manuel. Mais en parallèle, il fait aussi des exercices pour consolider ce qu’il a appris. Lorsqu'il rencontre des difficultés ou échoue dans la résolution d'un problème, il se rend compte des erreurs qu'il a commises et apprend comment les corriger, formant ainsi un « mauvais livre de problèmes ». C'est en apprenant de ses erreurs que ses capacités de raisonnement s'améliorent encore.

Inspiré de ce processus, cet ouvrage explore comment les capacités de raisonnement d'un LLM bénéficient de la compréhension et de la correction des erreurs.

Adresse papier : https://arxiv.org/pdf/2310.20689.pdf

Plus précisément, les chercheurs ont d'abord généré des paires de données de correction d'erreur (appelées données de correction), puis ont utilisé Corriger les données pour peaufiner le LLM. Lors de la génération des données de correction : ce qui devait être réécrit, ils ont utilisé plusieurs LLM (y compris LLaMA et la famille de modèles GPT) pour collecter des chemins d'inférence inexacts (c'est-à-dire que la réponse finale était incorrecte), et ont ensuite utilisé GPT-4 comme " " Correcteur " pour générer des corrections pour ces raisonnements inexacts

Les corrections générées contiennent trois informations : (1) l'étape incorrecte dans la solution d'origine ; (2) une explication de la raison pour laquelle l'étape était incorrecte ; (3) comment corriger la solution originale pour arriver à la bonne réponse finale. Après avoir filtré les corrections avec des réponses finales incorrectes, une évaluation manuelle a montré que les données de correction présentaient une qualité suffisante pour la phase de mise au point ultérieure. Les chercheurs ont utilisé QLoRA pour affiner le LLM sur les données CoT et les données de correction, réalisant ainsi un « apprentissage à partir des erreurs » (LEMA).

La recherche montre que le LLM actuel peut utiliser une approche étape par étape pour résoudre des problèmes, mais ce processus de génération en plusieurs étapes ne signifie pas que le LLM lui-même possède de fortes capacités de raisonnement. En effet, ils ne peuvent qu'imiter le comportement superficiel du raisonnement humain sans vraiment comprendre la logique sous-jacente et les règles requises.

Ce manque de compréhension entraînera des erreurs dans le processus de raisonnement, l'aide d'un « modèle mondial » est donc nécessaire. Parce que le « modèle du monde » a a priori une conscience de la logique et des règles du monde réel. De ce point de vue, le cadre LEMA présenté dans cet article peut être considéré comme utilisant GPT-4 comme « modèle mondial » pour apprendre à des modèles plus petits à suivre ces logiques et règles, plutôt que de simplement imiter un comportement étape par étape.

Maintenant, jetons un coup d'œil aux étapes spécifiques de mise en œuvre de cette étude

Aperçu de la méthodologie

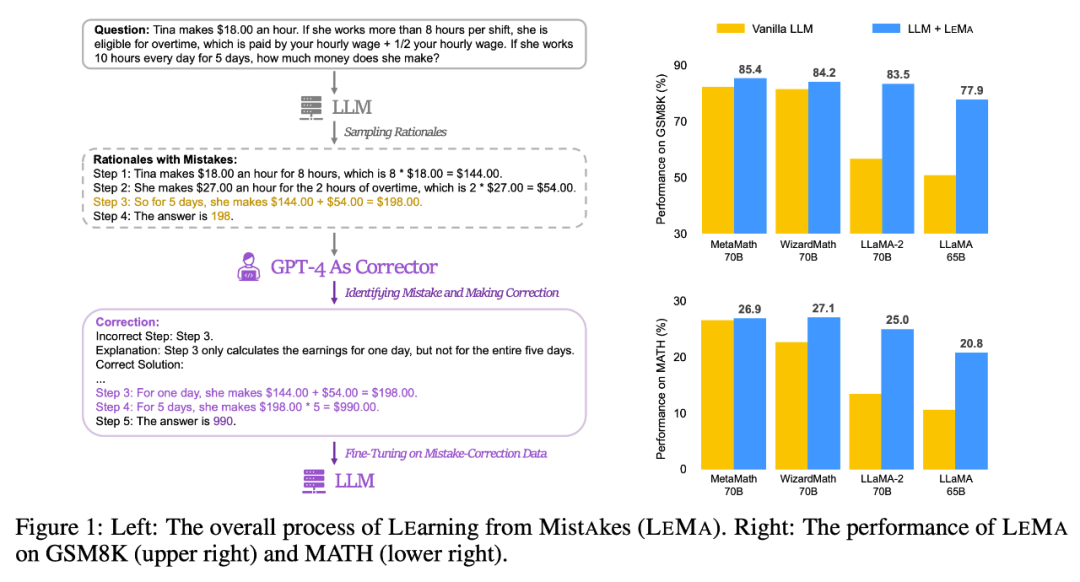
Veuillez regarder la figure 1 (à gauche) ci-dessous, qui montre le processus global de LEMA, y compris la génération de données corrigées : Obligatoire Il y a deux phases principales : la réécriture du contenu et la mise au point du LLM. La figure 1 (à droite) montre les performances de LEMA sur les ensembles de données GSM8K et MATH

Générer des données corrigées : ce qui doit être réécrit

À partir d'un exemple de questions et réponses 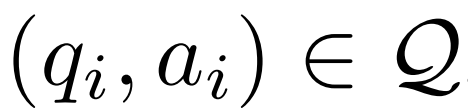, d'un modèle correcteur M_c et d'un modèle d'inférence M_r, le chercheur a généré des paires de données de correction d'erreur 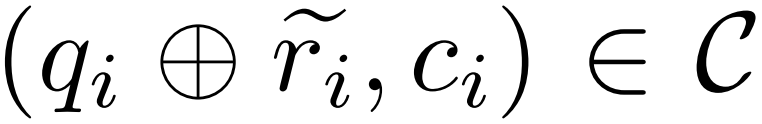, où 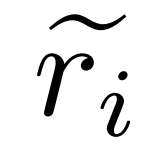représente le chemin d'inférence inexact de la question q_i et c_i représente la paire Correction de .

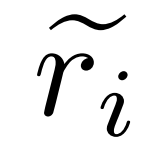Correction d'un chemin de raisonnement inexact . Le chercheur utilise d'abord le modèle d'inférence M_r pour échantillonner plusieurs chemins d'inférence pour chaque question q_i, puis retient uniquement les chemins qui ne mènent finalement pas à la bonne réponse a_i, comme le montre la formule suivante (1).

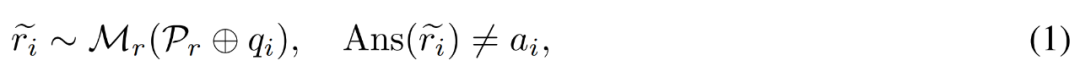
Construisez des correctifs pour les bugs. Pour la question q_i et le chemin de raisonnement inexact 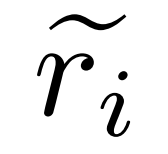, le chercheur utilise le modèle correcteur M_c pour générer une correction, puis vérifie la bonne réponse dans la correction, comme indiqué dans l'équation (2) ci-dessous.

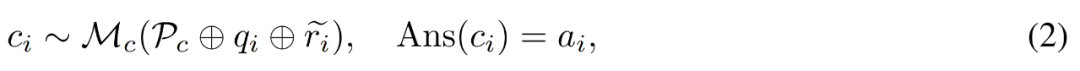
P_c comprend ici quatre exemples de correction d'erreur annotés pour guider le modèle de correcteur sur le type d'informations à inclure dans les corrections générées

Plus précisément, les corrections annotées incluent les trois types d'informations suivants :

• Étape d'erreur : quelle étape du cheminement de raisonnement d'origine s'est mal passée.
• Explication : Quel type d'erreur s'est produit à cette étape ;
• Solution correcte : Comment corriger le chemin de raisonnement inexact pour mieux résoudre le problème d'origine.

Veuillez consulter l'image ci-dessous, la figure 1 montre brièvement les invites utilisées pour générer des corrections

Générer une évaluation manuelle des corrections . Avant de générer des données plus volumineuses, nous avons d'abord évalué manuellement la qualité des corrections générées. Ils ont utilisé LLaMA-2-70B comme M_r et GPT-4 comme M_c et ont généré 50 paires de données corrigées des erreurs sur la base de l'ensemble de formation GSM8K.

Les chercheurs ont classé les correctifs en trois niveaux de qualité : excellent, bon et mauvais. Voici un exemple de trois niveaux

Les résultats de l'évaluation ont révélé que 35 correctifs de build sur 50 ont atteint une excellente qualité, 11 étaient bons et 4 étaient médiocres. Sur la base de cette évaluation, les chercheurs ont conclu que la qualité globale des corrections générées à l’aide de GPT-4 était suffisante pour poursuivre les étapes de réglage. Par conséquent, ils ont généré des corrections à plus grande échelle et ont utilisé toutes les corrections qui ont finalement conduit à la bonne réponse au LLM qui nécessitait un réglage fin.

C'est le LLM qui nécessite d'être peaufiné

Après avoir généré des données de correction : ce qui devait être réécrit, les chercheurs ont affiné le LLM pour évaluer si les modèles pouvaient apprendre de leurs erreurs. Ils effectuent principalement des comparaisons de performances selon les deux paramètres de réglage précis suivants.

La première consiste à affiner les données de la Chaîne de pensée (CoT). Les chercheurs affinent le modèle uniquement sur les données justifiant les questions. Bien qu'il existe des données annotées dans chaque tâche, elles utilisent en outre l'augmentation des données CoT. Les chercheurs ont utilisé GPT-4 pour générer davantage de chemins de raisonnement pour chaque question de l’ensemble de formation et filtrer les chemins avec des réponses finales incorrectes. Ils exploitent l’augmentation des données CoT pour créer une base de référence de réglage fin robuste qui utilise uniquement les données CoT et facilite les études d’ablation sur la taille des données qui contrôlent le réglage fin.

La seconde est la mise au point sur les données CoT + données corrigées. En plus des données CoT, les chercheurs ont également généré des données de correction d'erreurs pour un réglage fin (c'est-à-dire LEMA). Ils ont également mené des expériences d’ablation avec une taille de données contrôlée afin de réduire l’impact des incréments sur la taille des données.

L'exemple 5 et l'exemple 6 de l'annexe A montrent respectivement le format d'entrée-sortie des données CoT et des données de correction pour un réglage fin

Résultats expérimentaux

Les chercheurs ont prouvé à travers des résultats expérimentaux l'efficacité de LEMA sur cinq LLM open source et deux tâches de raisonnement mathématique difficiles

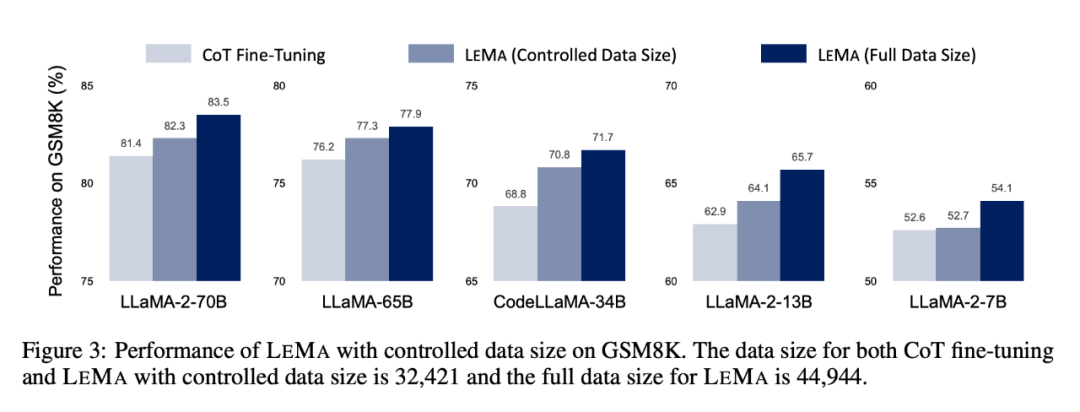
LEMA améliore constamment les performances dans une variété de LLM et de tâches, par rapport à un réglage fin uniquement sur les données CoT. Par exemple, LEMA utilisant LLaMA-2-70B a obtenu des résultats de 83,5 % et 25,0 % sur GSM8K et MATH respectivement, tandis que le réglage fin uniquement sur les données CoT a obtenu des résultats de 81,4 % et 23,6 % respectivement

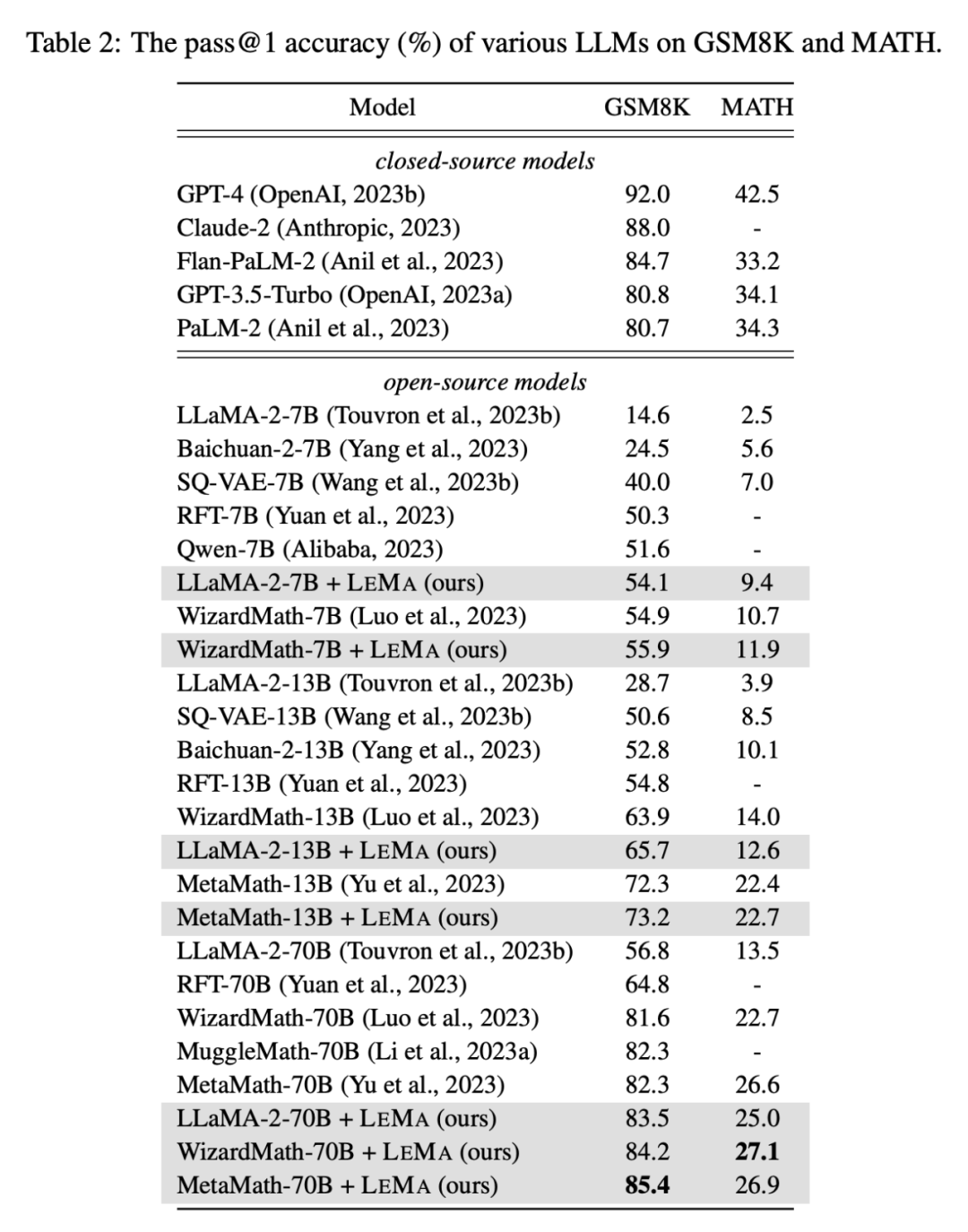
De plus , LEMA est compatible avec le LLM propriétaire : LEMA avec WizardMath-70B/MetaMath-70B atteint une précision pass@1 de 84,2 %/85,4 % sur GSM8K et 27,1 %/26,9 % sur MATH. Le taux de précision pass@1 dépasse les performances SOTA atteintes par de nombreux modèles open source sur ces tâches difficiles.

Des études d'ablation ultérieures montrent que LEMA surpasse toujours le réglage fin CoT seul avec la même quantité de données. Cela suggère que les données CoT et les données corrigées ne sont pas aussi efficaces, car la combinaison des deux sources de données produit plus d'améliorations que l'utilisation d'une seule source de données. Ces résultats expérimentaux et analyses mettent en évidence le potentiel de l’apprentissage à partir des erreurs pour améliorer les capacités d’inférence LLM.

Pour plus de détails sur la recherche, veuillez vous référer à l'article original

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!