
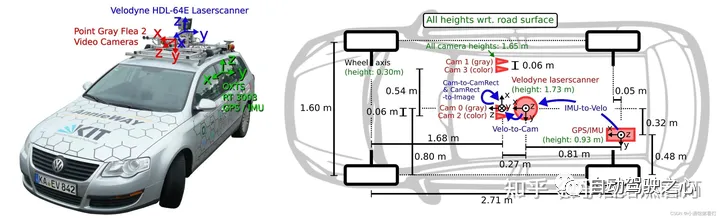
Cet article présente principalement plusieurs systèmes de coordonnées couramment utilisés dans la technologie de conduite autonome, et comment compléter la corrélation et la conversion entre eux, et enfin construire un modèle d'environnement unifié. L'objectif ici est de comprendre la conversion du véhicule en corps rigide de caméra (paramètres externes), la conversion de caméra en image (paramètres internes) et la conversion d'image en unité de pixel. La conversion de 3D en 2D aura une distorsion, une traduction, etc. Point clé : système de coordonnées du véhicule autonome
Système de coordonnées du corps de la caméraCe qui doit être réécrit est : le système de coordonnées du planSystème de coordonnées des pixelsDifficulté : la distorsion de l'image doit être prise en compte, et la suppression de la distorsion et la distorsion sont toutes deux compensées sur le plan image
La représentation des coordonnées homogènes est réalisée. Trois systèmes de coordonnées de capteurs
3.1.1 Système de coordonnées de l'image. (ou système de coordonnées de pixels) Pour les photos ou images stockées sur l'ordinateur, le coin supérieur gauche est généralement l'origine, la direction x positive est vers la droite et la direction y positive est vers le bas. est "pixel". Le système de coordonnées de l'image est un système de coordonnées bidimensionnel, étiqueté (Xv, Yv).
Le contenu qui doit être réécrit est : 3.1.2 Système de coordonnées de la caméra
Étant donné que l'axe x du système de coordonnées de l'image est à droite et l'axe y est vers le bas, le système de coordonnées de la caméra prend le centre de l'axe optique principal de la lentille comme origine. De manière générale, la direction positive est l'axe des x vers la droite, la direction positive est l'axe des y vers le bas et la direction positive est l'axe z vers l'avant. De cette façon, les directions x et y sont cohérentes avec la direction du système de coordonnées de l'image et la direction z représente la profondeur de champ. Le système de coordonnées de la caméra peut être exprimé comme (Xc, Yc)
Ce qui doit être réécrit est : 3.1.3 Ce qui doit être réécrit est : le système de coordonnées planes (ou système de coordonnées d'imagerie)
Pour pour pouvoir
description quantitative La relation cartographique de l'espace tridimensionnel à l'image bidimensionnelle, ce qui doit être réécrit est introduit dans le graphique : le système de coordonnées planes. Il s'agit d'une traduction du système de coordonnées de la caméra. Le centre est toujours sur l'axe optique principal de la caméra. La distance par rapport au centre de l'axe optique est égale à la distance focale de la caméra. l'image inversée réduite sur le film derrière le centre de l'axe optique, est le plan image réel (Xf, Yf). Cependant, pour faciliter l’analyse et le calcul, nous mettrons en place un plan image virtuel devant le centre de l’axe optique. L'image sur le plan de l'image virtuelle est une image verticale, de la même taille que l'image réelle inversée
Ce qui doit être réécrit est : Système de coordonnées du plan3.5 Système de coordonnées mondialEn fonction de la situation spécifique , il peut représenter n’importe quel objet introduit grâce à la caméra. L'unité est le mètre
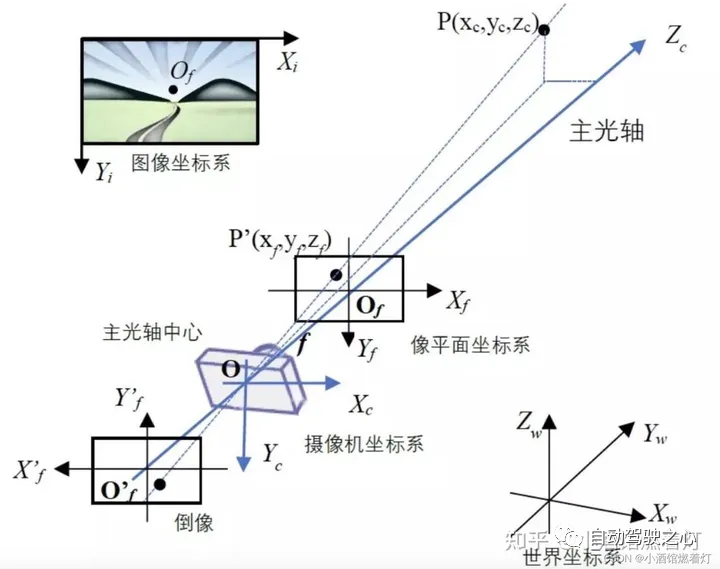
, système de coordonnées de caméra
Quatre systèmes de coordonnées Lidar 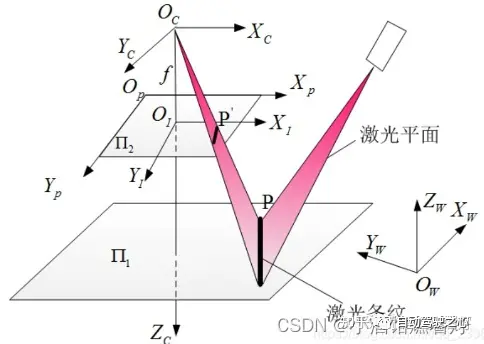
Lidar (Light Detection and Ranging) est un Technologie de télédétection , qui utilise des faisceaux laser pour mesurer la distance aux objets. Il émet des rayons dans une rotation de 360 degrés et forme des nuages électriques basés sur différentes réflexions de différentes réflectivités cibles. Dans le domaine de la conduite autonome et de la robotique, le Lidar est souvent utilisé comme capteur principal pour obtenir des informations 3D sur l'environnement. Dans la plupart des cas, le système de coordonnées Lidar est droitier, mais la définition spécifique peut varier en fonction du fabricant du Lidar. Axe X : pointe généralement devant le Lidar. Lorsque le faisceau laser est tiré directement vers l'avant, la mesure de la distance depuis cette direction produit une valeur positive sur l'axe X. Axe Y : pointe généralement vers le côté gauche du Lidar. Lorsque le faisceau laser est tiré directement vers la gauche, la mesure de distance dans cette direction produit une valeur positive sur l'axe Y. Axe Z : pointe généralement vers le haut du Lidar, perpendiculaire aux axes X et Y. Les mesures de hauteur sont généralement prises le long de l'axe Z, les valeurs positives représentant l'objet étant plus haut que le dispositif Lidar et les valeurs négatives le représentant étant inférieur au dispositif Lidar. Choisissez un système de coordonnées de référence dans l'environnement général pour décrire les positions des capteurs et des objets Ce système de coordonnées est appelé le système de coordonnées mondial en général ; fait référence à la carrosserie du véhicule Le centre de l'essieu arrière est l'origine (car le centre de l'essieu arrière ne changera pas par rapport au balancement de la voiture) , le système de coordonnées spatiales de l'avant supérieur gauche ou de l'avant supérieur droit, la gauche (droite) est généralement horizontale, l'avant est généralement longitudinale et la partie supérieure fait référence au sol. Dans l'espace ci-dessus, le système de coordonnées se déplace avec le mouvement de la voiture. Toutes les cibles en aval qui doivent être détectées et sorties doivent se trouver sous le système de coordonnées du véhicule autonome. La cible en perspective BEV fait également référence à ce système de coordonnées Généralement, le système de coordonnées spatiales tridimensionnelles. utilise trois axes orthogonaux X, Y, Z représentent la position de l'objet, et l'angle de rotation (angle de roulis, angle de tangage, angle de lacet) autour de ces trois axes orthogonaux représente l'attitude de l'objet. Le système de coordonnées temporelles n'a qu'une seule dimension. Pour faciliter l’expression, nous discutons généralement séparément des coordonnées spatiales et des coordonnées temporelles. point principal de la caméra, distance focale de la caméra et coefficient de distorsion. Les paramètres internes sont généralement donnés par le commerçant, et un calibrage de la caméra peut également être effectué. Dans les applications de conduite autonome, les paramètres internes de la caméra sont constants et ne changeront pas pendant l'utilisation, mais ils doivent être calibrés avant utilisation. Le processus de prise de vue de la caméra peut être résumé comme le processus de cartographie du système de coordonnées de la caméra 3D vers le système de coordonnées de la caméra 2D. Ce qui doit être réécrit est : le système de coordonnées planes, puis le processus de cartographie vers le système de coordonnées de l'image. 6.2 Distance focale (f)
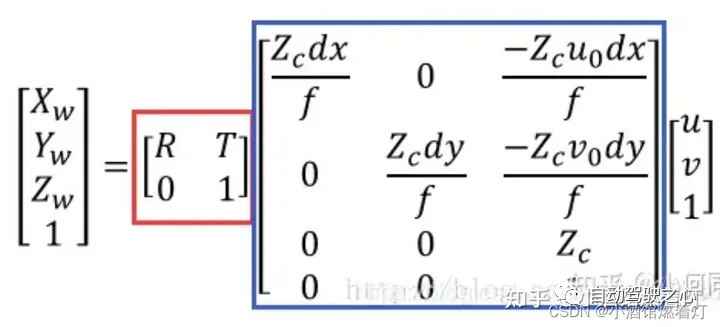
Cette matrice est souvent appelée matrice de paramètres internes ou matrice de caméra. Déduire la position de l'objet dans le système de coordonnées de la caméra tridimensionnelle à travers l'image bidimensionnelle, par exemple pour obtenir des informations sur la distance et la profondeur. Obtenez des informations de distance tridimensionnelles à partir d'une image bidimensionnelle Si devez obtenir la position de l'objet dans le système de coordonnées mondial , vous devez également connaître la pose de la caméra dans le système de coordonnées mondial . Cette représentation de pose est appelée le paramètre externe de la caméra, appelé paramètre externe, qui est utilisé pour déterminer la relation de position relative entre les coordonnées de la caméra et le système de coordonnées mondial. Dans les applications de conduite autonome, l’obtention de cette relation de position nécessite une série de travaux d’étalonnage et de positionnement. La caméra est une matrice de rotation + translation par rapport à d'autres systèmes de coordonnées, dans laquelle le paramètre externe de rotation est l'angle d'Euler mentionné ci-dessus [lacet, patch, roulis], l'ordre de rotation est généralement (z-y-x), degré unitaire de translation externe ; Le paramètre est la traduction de la caméra vers le système de coordonnées cible Distance, unité mètre Relation et conversion : - Puisque le véhicule se déplace dans le monde, la relation entre le système de coordonnées du véhicule autonome et le système de coordonnées mondial change dans le temps. - Afin d'effectuer une conversion entre ces deux systèmes de coordonnées, une matrice de transformation ou transformation (constituée généralement d'une rotation et d'une translation) est généralement nécessaire. Cette conversion peut être obtenue grâce à divers capteurs (tels que GPS, IMU, lidar) et algorithmes (tels que SLAM). - La transformation peut être exprimée sous la forme d'une matrice de coordonnées homogène 4x4, permettant de passer d'un système de coordonnées à un autre. Dans la plupart des cas, le système de coordonnées du véhicule autonome et le système de coordonnées mondial sont les mêmes, et cet article comprend également cela transformation de rotation plus transformation de translation du système de coordonnées, et il en va de même pour la relation de conversion du système de coordonnées mondial au système de coordonnées de la caméra. La rotation de différents angles autour de différents axes entraîne différentes matrices de rotation. Schéma de principe de la rotation θ autour de l'axe Z : Grâce à la relation de conversion finale, un point de coordonnées tridimensionnel peut trouver le point de pixel correspondant dans l'image. Cependant, à l'inverse, cela devient un problème de trouver le point correspondant dans l'espace tridimensionnel à travers un point de l'image, car on ne connaît pas la valeur du côté gauche de l'équation La case rouge est la paramètre externe, R et T sont respectivement les quantités de rotation et de translation. Les paramètres internes sont des attributs inhérents à la caméra, qui sont en réalité la distance focale f et la taille des pixels dx,dy. Évidemment, il représente la distance entre le point et l'axe optique. trie les différents systèmes de coordonnées de la conduite autonome, montre la relation entre les différents systèmes de coordonnées de la conduite autonome et obtient enfin la relation entre le système de coordonnées de pixels et le système de coordonnées mondial. Lien original : https://mp.weixin.qq.com/s/tTRCjZBRZcnb59nX3FRR8w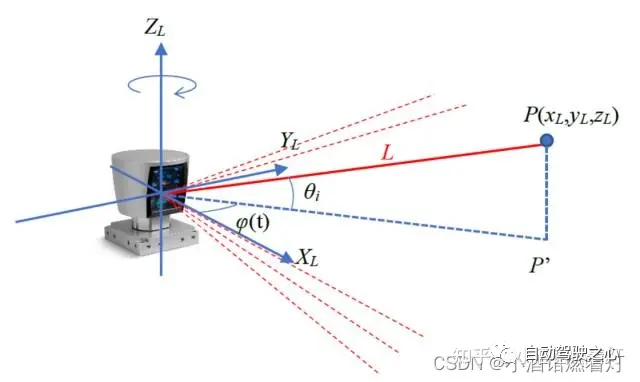
4.1 Définition
4.2 Importance
Le système de coordonnées à cinq véhicules
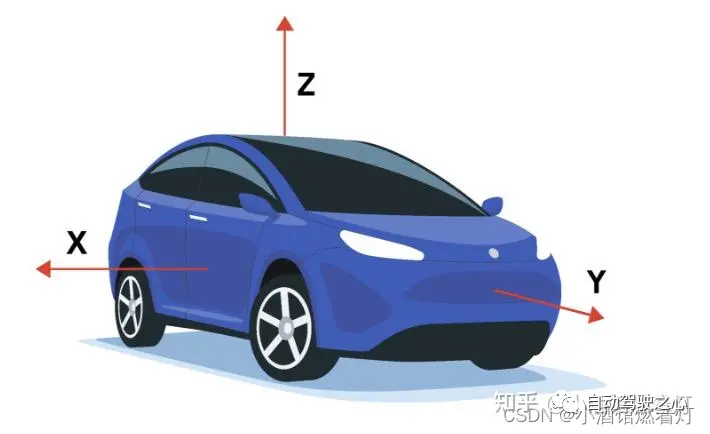
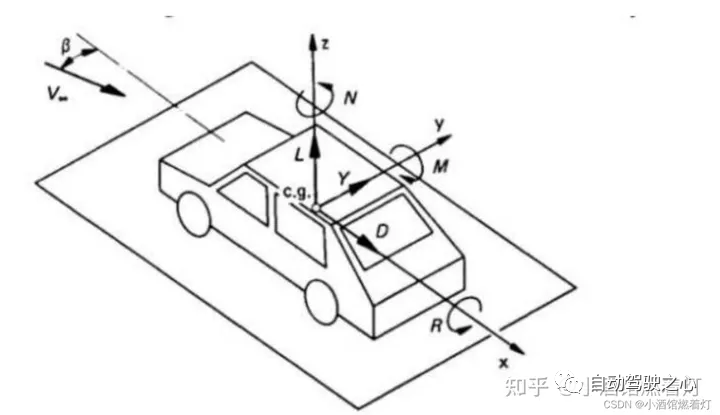
6 Paramètres internes et externes de la caméra
6.1 Paramètres internes de la caméra
Les paramètres internes sont utilisés pour déterminer la relation de projection de la caméra de l'espace tridimensionnel à l'image bidimensionnelle. Il contient principalement trois paramètres :
Elle décrit la distance
entre le capteur d'image et l'objectif de l'appareil photo. Généralement représenté par deux paramètres (
C'est un point de l'image, généralement proche du centre de l'image. C'est le point 2D correspondant à un point dans l'espace 3D lorsqu'il est projeté sur le plan image.
est généralement représenté par deux paramètres (
L'objectif d'un véritable appareil photo peut introduire une distorsion, provoquant une distorsion de l'image. Les distorsions courantes incluent la distorsion radiale et la distorsion tangentielle.
Le coefficient de distorsion radiale couramment utilisé est (
6.5 Paramètres extrinsèques de la caméra
Sept systèmes de coordonnées de véhicules et système de coordonnées mondiales
7.1 Système de coordonnées du véhicule (Système de coordonnées du véhicule)
Il s'agit d'un système de coordonnées fixe sur le véhicule.
7.2 Système de coordonnées mondial
Il s'agit d'un système de coordonnées global fixe utilisé pour décrire les objets et les véhicules dans l'environnement.
Relation de conversion entre les huit systèmes de coordonnées
8.1 Du système de coordonnées mondial à le système de coordonnées de la caméra
La transformation du système de coordonnées entre les objets peut représenter la 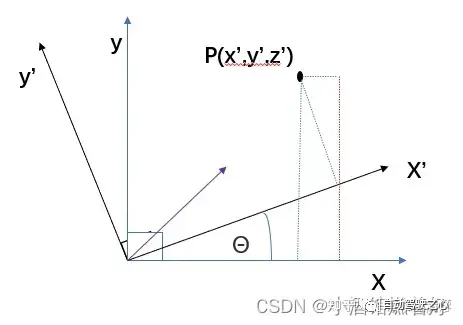
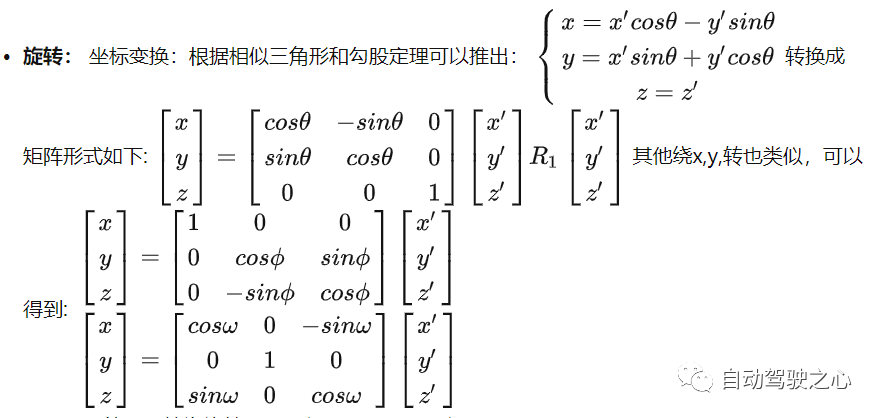
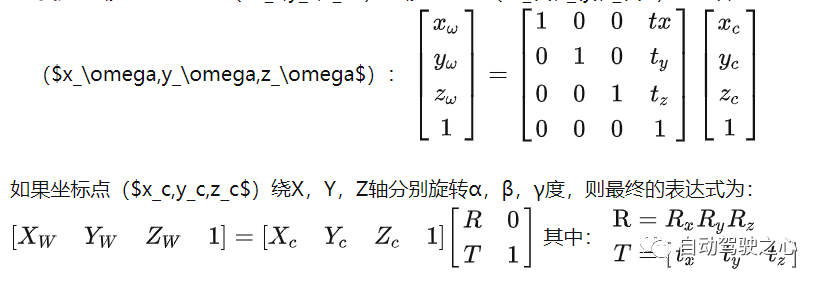
8.2 Système de coordonnées de la caméra au système de coordonnées de l'image
Du système de coordonnées de la caméra au système de coordonnées de l'image, il appartient à la relation de projection en perspective, passant de la 3D à la 2D. Il peut également être considéré comme un modèle de changement du modèle sténopé. Satisfaire le théorème de similarité des triangles.
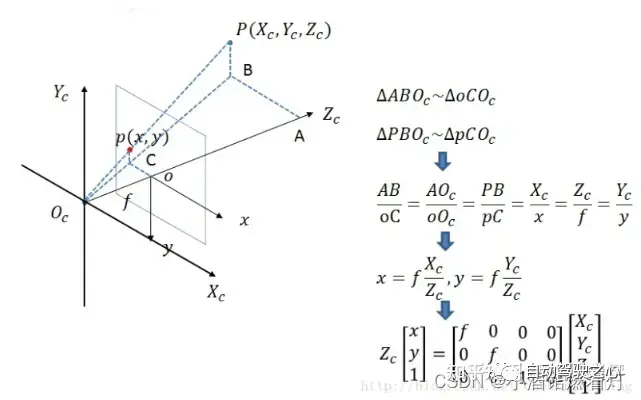
8.3 Système de coordonnées d'image en système de coordonnées de pixels
Dans ce cas, contrairement à la transformation du système de coordonnées précédente, il n'y a pas de transformation de rotation pour le moment, mais la position et la taille de l'origine des coordonnées sont incohérentes, donc une conception télescopique est requise Transformation et transformation de traduction
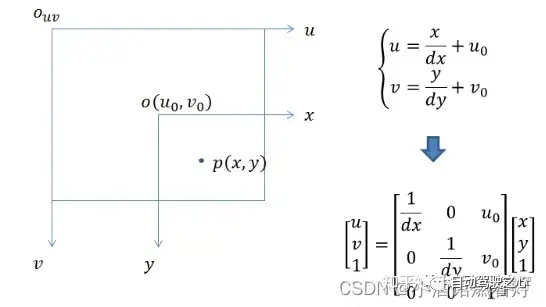
8.4 La relation entre les quatre systèmes de coordonnées
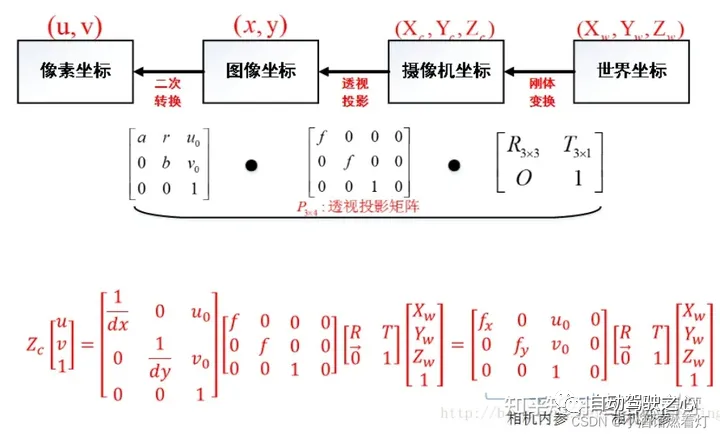
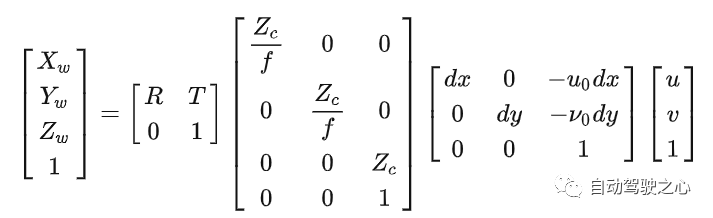
Neuf résumé

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Quelles compétences sont nécessaires pour travailler dans l'industrie PHP ?
Quelles compétences sont nécessaires pour travailler dans l'industrie PHP ?
 Éléments de base des présentations
Éléments de base des présentations
 Touche de raccourci de veille
Touche de raccourci de veille
 Format de courrier électronique professionnel
Format de courrier électronique professionnel
 Combien de personnes pouvez-vous élever sur Douyin ?
Combien de personnes pouvez-vous élever sur Douyin ?
 Que signifient les composants électroniques ?
Que signifient les composants électroniques ?
 Que signifie une startup héritée ?
Que signifie une startup héritée ?
 Comment transformer deux pages en un seul document Word
Comment transformer deux pages en un seul document Word