Plus polyvalent et efficace, l'optimiseur WSAM développé par Ant a été sélectionné par KDD Oral

La capacité de généralisation des réseaux de neurones profonds (DNN) est étroitement liée à la planéité des points extrêmes, c'est pourquoi l'algorithme de minimisation sensible à la netteté (SAM) a émergé pour trouver des points extrêmes plus plats afin d'améliorer la capacité de généralisation. Cet article réexamine la fonction de perte de SAM et propose une méthode plus générale et plus efficace, WSAM, pour améliorer la planéité des points extrêmes d'entraînement en utilisant la planéité comme terme de régularisation. Des expériences sur divers ensembles de données publiques montrent que par rapport à l'optimiseur d'origine, SAM et ses variantes, WSAM atteint de meilleures performances de généralisation dans la grande majorité des cas. WSAM a également été largement adopté dans les paiements numériques internes d'Ant, la finance numérique et d'autres scénarios et a obtenu des résultats remarquables. Cet article a été accepté comme article oral par KDD '23.

• Adresse papier : https://arxiv.org/pdf/2305.15817.pdf
• Adresse code : https://github.com/in Telli Gentil - machine-learning/dlrover/tree/master/atorch/atorch/optimizers

Avec le développement de la technologie d'apprentissage profond, les DNN hautement surparamétrés ont obtenu d'excellents résultats dans divers scénarios d'apprentissage automatique tels que le CV et la PNL. succès. Bien que les modèles surparamétrés aient tendance à surajuster les données d’entraînement, ils ont généralement de bonnes capacités de généralisation. Le secret de la généralisation attire de plus en plus d’attention et est devenu un sujet de recherche populaire dans le domaine de l’apprentissage profond.

Les dernières recherches montrent que la capacité de généralisation est étroitement liée à la planéité des points extrêmes. En d’autres termes, la présence de points extrêmes plats dans le « paysage » de la fonction de perte permet des erreurs de généralisation plus faibles. La minimisation sensible à la netteté (SAM) [1] est une technique permettant de trouver des points extrêmes plus plats et est considérée comme l'une des directions techniques les plus prometteuses actuellement. La technologie SAM est largement utilisée dans de nombreux domaines tels que la vision par ordinateur, le traitement du langage naturel et l'apprentissage à deux couches, et surpasse considérablement les méthodes de pointe précédentes dans ces domaines

Afin d'explorer des minimums plus plats, SAM définit une fonction de perte La planéité de L en w est la suivante :

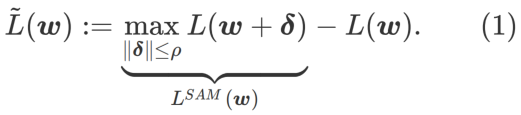
GSAM [2] a prouvé que 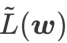est une approximation de la valeur propre maximale de la matrice de Hesse au point extrême local, indiquant que 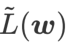est effectivement plat (raide) Mesure efficace. Cependant 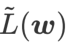ne peut être utilisé que pour trouver des zones plus plates plutôt que des points minimaux, ce qui peut faire converger la fonction de perte vers un point où la valeur de perte est encore grande (bien que la zone environnante soit plate). Par conséquent, SAM utilise 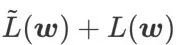, c'est-à-dire 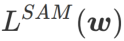comme fonction de perte. Cela peut être considéré comme un compromis entre trouver une surface plus plane et une valeur de perte plus petite entre 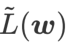et 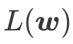, où les deux ont le même poids.

Cet article repense la construction de 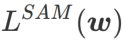et traite 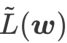comme un terme de régularisation. Nous avons développé un algorithme plus général et efficace appelé WSAM (Weighted Sharpness-Aware Minimization). Sa fonction de perte ajoute un terme de planéité pondéré 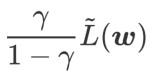comme terme de régularisation, dans lequel l'hyperparamètre 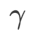contrôle le poids de planéité. Dans le chapitre d'introduction à la méthode, nous avons montré comment utiliser 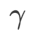pour guider la fonction de perte afin de trouver des points extrêmes plus plats ou plus petits. Nos principales contributions peuvent être résumées comme suit.

• Nous proposons WSAM, qui traite la planéité comme un terme de régularisation et donne des poids différents entre les différentes tâches. Nous proposons une technique de « découplage des poids » pour gérer le terme de régularisation dans la formule de mise à jour, visant à refléter avec précision la planéité de l'étape actuelle. Lorsque l'optimiseur sous-jacent n'est pas SGD, comme SGDM et Adam, la forme de WSAM diffère considérablement de celle de SAM. Les expériences d'ablation montrent que cette technique améliore les performances dans la plupart des cas.
• Nous avons vérifié l'efficacité de WSAM sur les tâches courantes sur des ensembles de données publics. Les résultats expérimentaux montrent que par rapport à SAM et ses variantes, WSAM présente de meilleures performances de généralisation dans la plupart des situations.

Connaissances préliminaires

SAM est une technique permettant de résoudre le problème d'optimisation minimax de 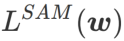défini par la formule (1).

Premièrement, SAM utilise une expansion de Taylor du premier ordre autour de w pour approximer le problème de maximisation de la couche interne, c'est-à-dire ,

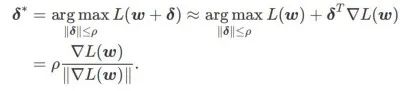
Deuxièmement, SAM met à jour w en prenant le gradient approximatif de 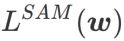, c'est-à-dire

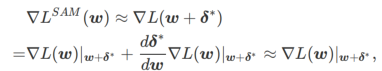
La deuxième approximation consiste à accélérer le calcul. D'autres optimiseurs basés sur le gradient (appelés optimiseurs de base) peuvent être incorporés dans le cadre général de SAM, voir Algorithme 1 pour plus de détails. En changean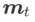t et 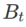dans l'algorithme 1, nous pouvons obtenir différents optimiseurs de base, tels que SGD, SGDM et Adam, voir l'onglet 1. Notez que l'algorithme 1 revient au SAM d'origine du document SAM [1] lorsque l'optimiseur de base est SGD.

Introduction à la méthode

Détails de conception de WSAM

Ici, nous donnons la définition formelle de 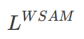, qui consiste en une perte régulière et un terme de planéité. De la formule (1), nous avons

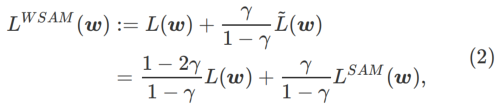
Parmi eux 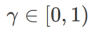. Quand 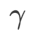=0, 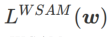dégénère en perte régulière ; quand 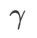=1/2, 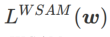équivaut à 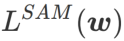; de la même manière que SAM, il est plus facile de trouver des points avec des courbures plus petites plutôt que des valeurs de perte plus petites et vice versa ;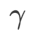 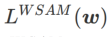Un cadre général pour WSAM contenant différents optimiseurs de base peut être implémenté en choisissant différents

et 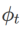, voir Algorithme 2. Par exemple, lorsque 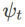et , on obtient WSAM dont l'optimiseur de base est SGD, voir Algorithme 3. Ici, nous adoptons une technique de « découplage des poids », où le terme de planéité n'est pas intégré à l'optimiseur de base pour calculer les gradients et mettre à jour les poids, mais est calculé indépendamment (le dernier terme sur la ligne 7 de l'algorithme 2). De cette manière, l’effet de régularisation reflète uniquement la planéité du pas en cours sans information supplémentaire. A titre de comparaison, l'algorithme 4 donne un WSAM sans « découplage de poids » (appelé Coupled-WSAM). Par exemple, si l'optimiseur sous-jacent est SGDM, le terme de régularisation de Coupled-WSAM est une moyenne mobile exponentielle de planéité. Comme le montre la section expérimentale, le « découplage des poids » peut améliorer les performances de généralisation dans la plupart des cas.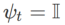

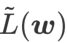
Fig. 1 montre le processus de mise à jour WSAM sous différentes 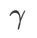valeurs. Lorsque 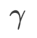, 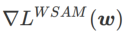est compris entre 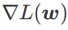et 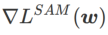et s'écarte progressivement de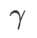 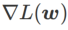à mesure que augmente.

Exemple simple

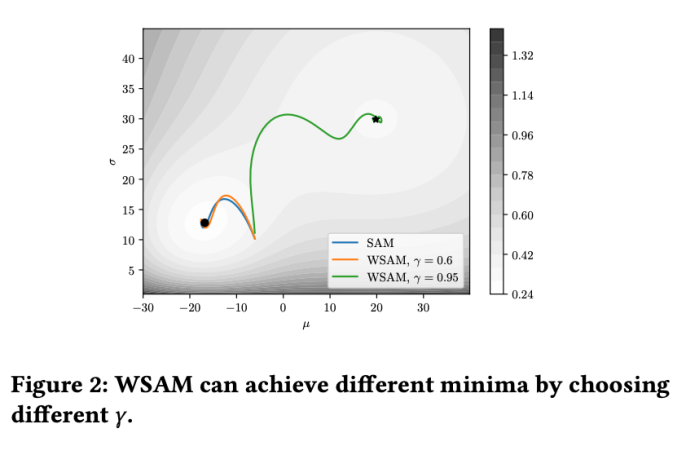
Pour mieux illustrer l'effet et les avantages de γ dans WSAM, nous avons mis en place un exemple simple en deux dimensions. Comme le montre la figure 2, la fonction de perte a un point extrême relativement inégal dans le coin inférieur gauche (position : (-16,8, 12,8), valeur de perte : 0,28) et un point extrême plat dans le coin supérieur droit (position : (19,8, 29,9), valeur de perte : 0,36). 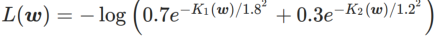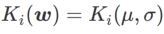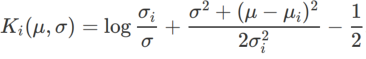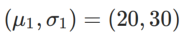La fonction de perte est définie comme : , où est la divergence KL entre le modèle gaussien univarié et deux distributions normales, c'est-à-dire , où et .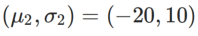

Nous utilisons SGDM avec un élan de 0,9 comme optimiseur de base et définissons 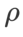=2 pour SAM et WSAM. À partir du point initial (-6, 10), la fonction de perte est optimisée en 150 étapes en utilisant un taux d'apprentissage de 5. SAM converge vers le point extrême avec une valeur de perte plus faible mais plus inégale, similaire à WSAM avec 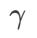=0,6. Cependant, 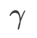=0,95 fait converger la fonction de perte vers un point extrême plat, indiquant qu'une régularisation plus forte de la planéité joue un rôle.

Expériences

Nous avons mené des expériences sur diverses tâches pour vérifier l'efficacité de WSAM.

Classification d'images

Nous avons d'abord étudié l'effet de WSAM sur les modèles d'entraînement à partir de zéro sur les ensembles de données Cifar10 et Cifar100. Les modèles que nous avons sélectionnés incluent ResNet18 et WideResNet-28-10. Nous formons des modèles sur Cifar10 et Cifar100 en utilisant des tailles de lots prédéfinies de 128, 256 pour ResNet18 et WideResNet-28-10 respectivement. L'optimiseur de base utilisé ici est SGDM avec momentum 0.9. Selon les paramètres de SAM [1], chaque optimiseur de base exécute deux fois plus d'époques que l'optimiseur de classe SAM. Nous avons entraîné les deux modèles pendant 400 époques (200 époques pour l'optimiseur de classe SAM) et utilisé un planificateur de cosinus pour diminuer le taux d'apprentissage. Ici, nous n'utilisons pas d'autres méthodes avancées d'augmentation des données telles que la découpe et l'AutoAugment.

Pour les deux modèles, nous utilisons une recherche de grille conjointe pour déterminer le taux d'apprentissage et le coefficient de dégradation du poids de l'optimiseur de base et les maintenons constants pour les expériences suivantes de l'optimiseur de classe SAM. Les plages de recherche du taux d'apprentissage et du coefficient de perte de poids sont respectivement {0,05, 0,1} et {1e-4, 5e-4, 1e-3}. Puisque tous les optimiseurs de classe SAM ont un hyperparamètre 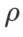(taille du quartier), nous recherchons ensuite le meilleur 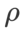sur l'optimiseur SAM et utilisons la même valeur pour les autres optimiseurs de classe SAM. La plage de recherche de 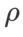est {0,01, 0,02, 0,05, 0,1, 0,2, 0,5}. Enfin, nous avons recherché les hyperparamètres uniques d'autres optimiseurs de classe SAM, et la plage de recherche provenait de la plage recommandée de leurs articles originaux respectifs. Pour GSAM [2], nous recherchons dans la plage {0,01, 0,02, 0,03, 0,1, 0,2, 0,3}. Pour ESAM [3], nous recherchons dans la plage de {0,4, 0,5, 0,6}, 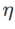dans la plage de {0,4, 0,5, 0,6} et 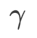dans la plage de {0,4, 0,5 , 0,6}. Pour WSAM, nous recherchons dans la plage {0,5, 0,6, 0,7, 0,8, 0,82, 0,84, 0,86, 0,88, 0,9, 0,92, 0,94, 0,96}. Nous avons répété l'expérience 5 fois en utilisant différentes graines aléatoires et calculé l'erreur moyenne et l'écart type. Nous menons des expériences sur un GPU NVIDIA A100 monocarte. Les hyperparamètres de l'optimiseur pour chaque modèle sont résumés dans le tableau 3.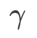

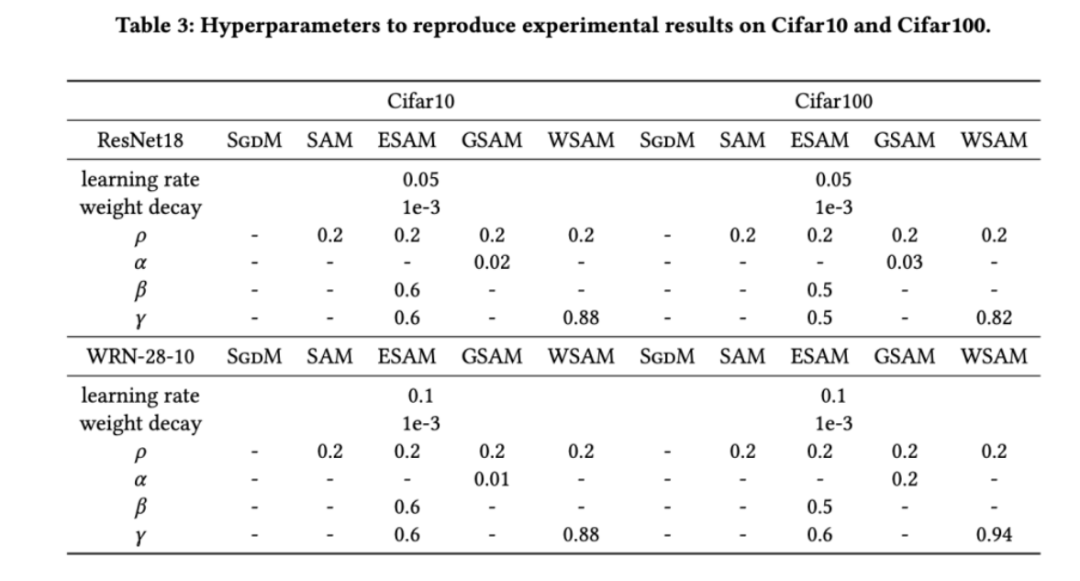
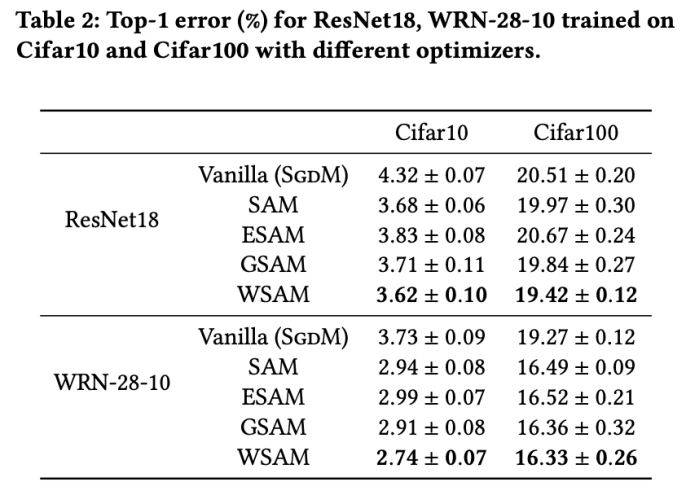
L'onglet 2 donne le premier taux d'erreur de ResNet18, WRN-28-10 sur l'ensemble de tests sur Cifar10 et Cifar100 sous différents optimiseurs. Par rapport à l'optimiseur de base, l'optimiseur de classe SAM améliore considérablement les performances. Dans le même temps, WSAM est nettement meilleur que les autres optimiseurs de classe SAM.

Formation supplémentaire sur ImageNet

Nous menons en outre des expériences sur l'ensemble de données ImageNet en utilisant la structure de réseau Data-Efficient Image Transformers. Nous reprenons un point de contrôle de base DeiT pré-entraîné, puis poursuivons la formation pendant trois époques. Le modèle est entraîné en utilisant une taille de lot de 256, l'optimiseur de base est SGDM avec une impulsion de 0,9, le coefficient de décroissance du poids est de 1e-4 et le taux d'apprentissage est de 1e-5. Nous avons répété l'exécution 5 fois sur un GPU NVIDIA A100 à quatre cartes et calculé l'erreur moyenne et l'écart type

Nous avons recherché le meilleur 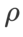de SAM en {0.05, 0.1, 0.5, 1.0,⋯, 6.0} . L'optimal 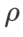=5,5 est utilisé directement dans d'autres optimiseurs de classe SAM. Après cela, nous recherchons le meilleur de GSAM en {0,01, 0,02, 0,03, 0,1, 0,2, 0,3} et le meilleur 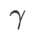de WSAM entre 0,80 et 0,98 avec un pas de 0,02.

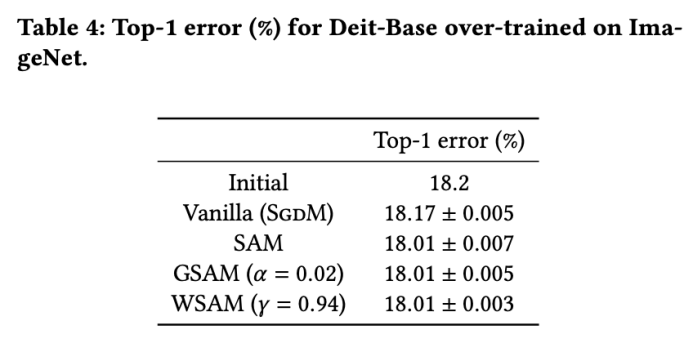
Le taux d'erreur initial du modèle est de 18,2 %, et après trois époques supplémentaires, le taux d'erreur est indiqué dans l'onglet 4. Nous ne trouvons pas de différences significatives entre les trois optimiseurs de type SAM, mais ils surpassent tous l'optimiseur de base, ce qui indique qu'ils peuvent trouver des points extrêmes plus plats et avoir de meilleures capacités de généralisation.

Robustesse au bruit d'étiquette

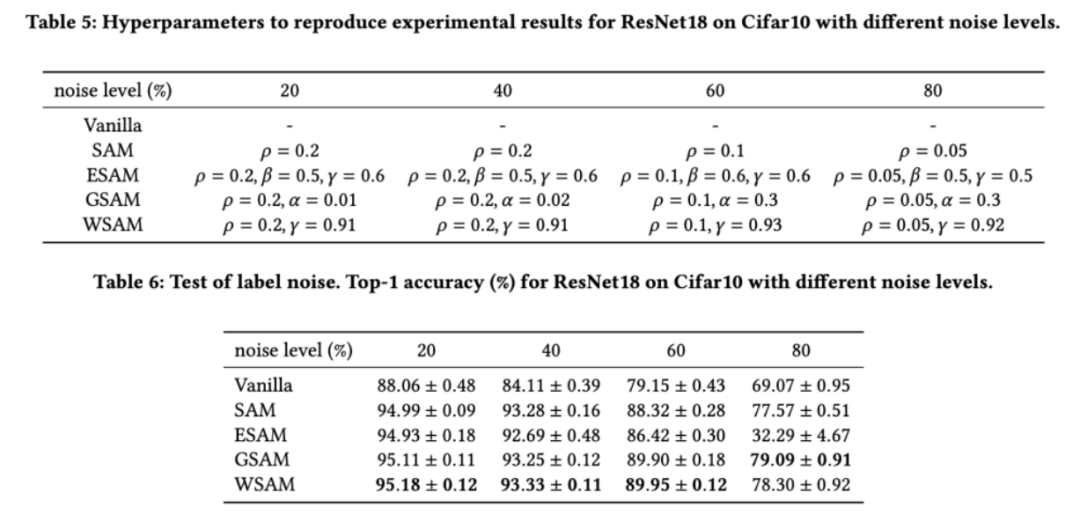
Comme le montrent des études précédentes [1, 4, 5], les optimiseurs de classe SAM montrent une bonne robustesse lorsque le bruit d'étiquette existe dans l'ensemble d'entraînement. Ici, nous comparons la robustesse de WSAM avec SAM, ESAM et GSAM. Nous entraînons ResNet18 sur l'ensemble de données Cifar10 pendant 200 époques et injectons du bruit d'étiquette symétrique avec des niveaux de bruit de 20 %, 40 %, 60 % et 80 %. Nous utilisons SGDM avec une impulsion de 0,9 comme optimiseur de base, une taille de lot de 128, un taux d'apprentissage de 0,05, un coefficient de décroissance du poids de 1e-3 et un planificateur de cosinus pour diminuer le taux d'apprentissage. Pour chaque niveau de bruit d'étiquette, nous avons effectué une recherche de grille sur le SAM dans la plage {0,01, 0,02, 0,05, 0,1, 0,2, 0,5} pour déterminer une valeur universelle 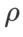. Nous recherchons ensuite individuellement d'autres hyperparamètres spécifiques à l'optimiseur pour trouver des performances de généralisation optimales. Nous listons les hyperparamètres nécessaires pour reproduire nos résultats dans le Tab 5. Nous présentons les résultats du test de robustesse dans le Tab. 6. WSAM a généralement une meilleure robustesse que SAM, ESAM et GSAM.

Impact de la géométrie d'exploration

Les optimiseurs de type SAM peuvent être combinés avec des techniques telles que ASAM [4] et Fisher SAM [5] pour ajuster de manière adaptative la forme du quartier d'exploration. Nous menons des expériences sur WRN-28-10 sur Cifar10 pour comparer les performances de SAM et WSAM lors de l'utilisation des méthodes d'information adaptatives et Fisher, respectivement, afin de comprendre comment la géométrie de la région d'exploration affecte les performances de généralisation des optimiseurs de type SAM.

À l'exception des paramètres 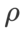et 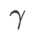, nous avons réutilisé la configuration en classification d'images. Selon des études antérieures [4, 5], les 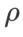de ASAM et Fisher SAM sont généralement plus grands. Nous recherchons le meilleur 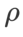en {0.1, 0.5, 1.0,…, 6.0}, et le meilleur 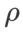pour ASAM et Fisher SAM est 5.0. Après cela, nous avons recherché le meilleur 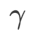de WSAM entre 0,80 et 0,94 avec un pas de 0,02, et le meilleur 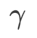des deux méthodes était de 0,88.

Étonnamment, comme le montre l'onglet 7, le WSAM de base montre une meilleure généralisation, même parmi plusieurs candidats. Par conséquent, nous vous recommandons simplement d’utiliser WSAM avec une 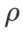baseline fixe.

Expérience d'ablation

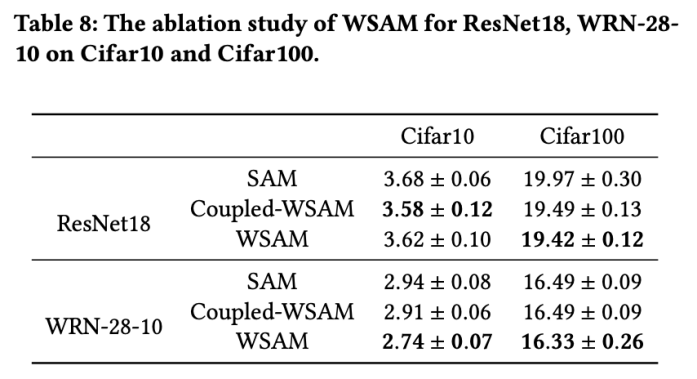
Dans cette section, nous menons des expériences d'ablation pour acquérir une compréhension approfondie de l'importance de la technique de « découplage du poids » dans WSAM. Comme décrit dans les détails de conception de WSAM, nous comparons la variante WSAM sans « découplage de poids » (algorithme 4) Couplé-WSAM avec la méthode d'origine.

Les résultats sont présentés dans l'onglet 8. Le WSAM couplé produit de meilleurs résultats que le SAM dans la plupart des cas, et le WSAM améliore encore les résultats dans la plupart des cas, démontrant l'efficacité de la technique de « découplage du poids ».

Analyse des points extrêmes

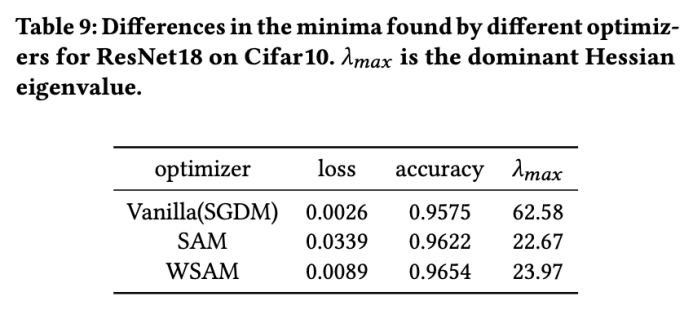
Ici, nous approfondissons davantage notre compréhension de l'optimiseur WSAM en comparant les différences entre les points extrêmes trouvés par les optimiseurs WSAM et SAM. La planéité (pente) aux points extrêmes peut être décrite par la valeur propre maximale de la matrice hessienne. Plus la valeur propre est grande, moins elle est plate. Nous utilisons l'algorithme Power Iteration pour calculer cette valeur propre maximale.

L'onglet 9 montre la différence entre les points extrêmes trouvés par les optimiseurs SAM et WSAM. Nous constatons que les points extrêmes trouvés par l'optimiseur Vanilla ont des valeurs de perte plus petites mais sont moins plats, tandis que les points extrêmes trouvés par SAM ont des valeurs de perte plus grandes mais sont plus plates, améliorant ainsi les performances de généralisation. Fait intéressant, les points extrêmes trouvés par WSAM ont non seulement des valeurs de perte beaucoup plus faibles que celles de SAM, mais ont également une planéité très proche de celle de SAM. Cela montre que dans le processus de recherche de points extrêmes, WSAM donne la priorité à des valeurs de perte plus faibles tout en essayant de rechercher des zones plus plates.

Sensibilité des hyperparamètres

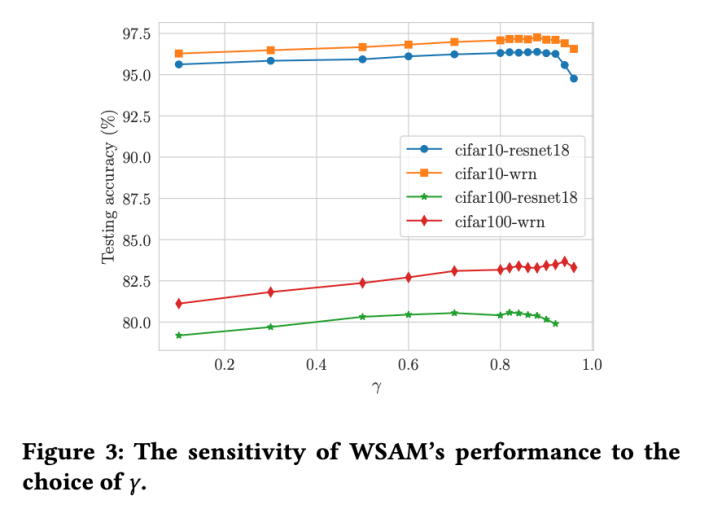
Par rapport à SAM, WSAM possède un hyperparamètre supplémentaire 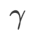pour mettre à l'échelle la taille du terme de degré plat (raide). Ici, nous testons la sensibilité des performances de généralisation de WSAM à cet hyperparamètre. Nous avons formé les modèles ResNet18 et WRN-28-10 à l'aide de WSAM sur Cifar10 et Cifar100, en utilisant une large gamme de valeurs 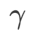. Comme le montre la Fig. 3, les résultats montrent que WSAM n'est pas sensible au choix de l'hyperparamètre 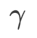. Nous avons également constaté que les performances de généralisation optimales de WSAM se situent presque toujours entre 0,8 et 0,95.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!