Quantifiez les activations, les poids et les gradients en 4 bits, ce qui devrait accélérer la formation des réseaux neuronaux.
Cependant, les méthodes de formation à 4 chiffres existantes nécessitent un format de nombre personnalisé, qui n'est pas pris en charge par le matériel moderne.
Récemment, l'équipe de Tsinghua Zhu Jun a proposé une méthode de formation Transformer qui utilise l'algorithme INT4 pour implémenter toutes les multiplications matricielles.
L'entraînement avec une précision INT4 ultra-faible est très difficile. Afin d’atteindre cet objectif, les chercheurs ont soigneusement analysé les structures spécifiques des activations et des gradients dans Transformer et ont proposé des quantificateurs dédiés.
Pour la propagation vers l'avant, les chercheurs ont identifié le défi des valeurs aberrantes et ont proposé le quantificateur Hadamard pour supprimer les valeurs aberrantes.
Pour la rétropropagation, ils exploitent la rareté structurelle des gradients en proposant un partitionnement de bits et utilisent des techniques d'échantillonnage fractionnaire pour quantifier avec précision les gradients.
Ce nouvel algorithme atteint une précision compétitive sur un large éventail de tâches, notamment la compréhension du langage naturel, la traduction automatique et la classification d'images.
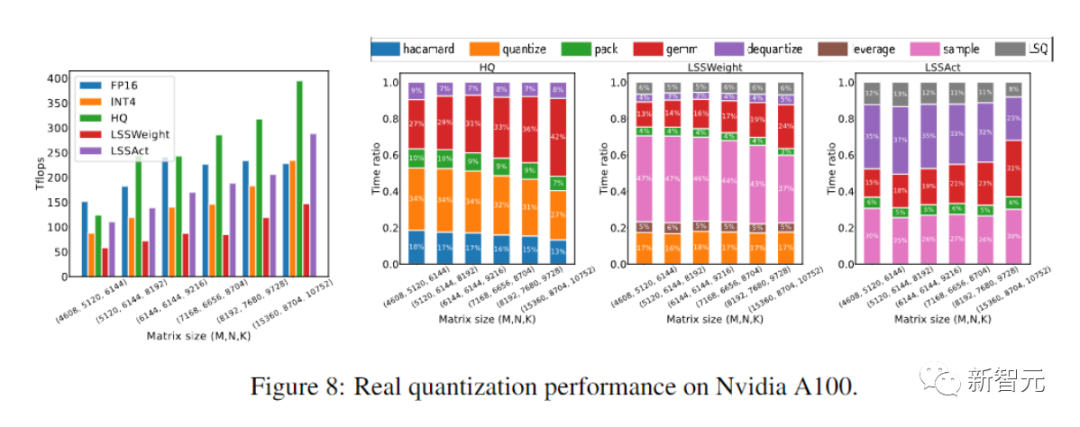
Le prototype d'opérateur linéaire est 2,2 fois plus rapide que les opérateurs similaires du FP16, et la vitesse de formation est augmentée de 35,1 %.
Photos
Adresse papier : https://arxiv.org/abs/2306.11987
Adresse code : https://github.com/xijiu9/Train_Transformers_with_INT4
La formation des réseaux de neurones est très exigeante en termes de calcul. La formation utilisant l’arithmétique de faible précision (formation entièrement quantifiée/FQT) devrait améliorer l’efficacité des calculs et de la mémoire.
La méthode FQT ajoute des quantificateurs et déquantificateurs au graphique de calcul original en pleine précision et remplace les opérations à virgule flottante les plus coûteuses par des opérations à virgule flottante de faible précision moins coûteuses.
La recherche FQT vise à réduire la précision numérique de l'entraînement sans trop sacrifier la vitesse ou la précision de convergence.
La précision numérique requise a été réduite de FP16 à FP8, INT32+INT8 et INT8+INT5.
La formation FP8 est implémentée dans le GPU Nvidia H100 avec le moteur Transformer, accélérant la formation de Transformer à grande échelle. La précision numérique de la formation récente est tombée à 4 chiffres.
Cependant, ces méthodes de formation 4 bits ne peuvent pas être utilisées directement pour l'accélération car elles nécessitent des formats de nombres personnalisés, qui ne sont pas pris en charge par le matériel moderne.
Tout d'abord, le quantificateur non différentiable en propagation vers l'avant rendra la situation de perte cahoteuse, et l'optimiseur basé sur le gradient peut facilement tomber dans un optimal local.
Deuxièmement, le dégradé n'est approximé qu'avec une faible précision. De tels gradients imprécis peuvent ralentir le processus d’entraînement et même rendre l’entraînement instable ou diverger.
Dans ce travail, les chercheurs ont proposé un nouvel algorithme de formation INT4 pour Transformer.
Images
Toutes les opérations linéaires coûteuses pour la formation de Transformer peuvent être écrites sous forme de multiplication matricielle (MM).
Cette forme MM nous permet de concevoir un quantificateur plus flexible, qui peut mieux se rapprocher de la multiplication matricielle FP32 en utilisant la structure spécifique des activations, des poids et des gradients dans Transformer.
Les avancées dans le domaine de l'algèbre linéaire numérique aléatoire (RandNLA) sont pleinement exploitées par ce quantificateur.
Pour la propagation vers l'avant, les chercheurs ont découvert que les valeurs aberrantes en matière d'activation sont la principale raison de la diminution de la précision.
Pour supprimer les valeurs aberrantes, ils ont proposé le quantificateur Hadamard, qui quantifie la version transformée de la matrice d'activation. Cette transformation est une matrice Hadamard diagonale par blocs, qui propage les informations contenues dans les valeurs aberrantes aux entrées voisines de la matrice, réduisant ainsi la plage numérique des valeurs aberrantes.
Pour la rétropropagation, ils exploitent la rareté structurelle du gradient d'activation. Les chercheurs ont découvert que certains jetons présentent des gradients très importants. Dans le même temps, les gradients de la plupart des autres jetons sont très uniformes, encore plus uniformes que les résidus quantifiés de grands gradients.
Images
Ainsi, au lieu de calculer tous les gradients, il est préférable d'économiser les ressources de calcul nécessaires au calcul des résidus de gradient les plus importants.
Afin de profiter de cette rareté, les chercheurs ont proposé un partitionnement de bits, qui divise le gradient de chaque jeton en 4 bits élevés et 4 bits faibles.
Ensuite, le gradient le plus informatif est sélectionné grâce à l'échantillonnage par score de levier, qui est une technique d'échantillonnage importante de RandNLA.
Pictures
En combinant les techniques de quantification de propagation vers l'avant et vers l'arrière, les chercheurs ont proposé un algorithme qui utilise INT4MM pour effectuer toutes les opérations linéaires dans Transformer, et ont évalué l'algorithme de formation de Transformer sur diverses tâches, y compris le langage naturel. compréhension, réponse aux questions, traduction automatique et classification d'images.
Leur algorithme atteint une précision compétitive ou supérieure par rapport aux algorithmes d'entraînement 4 bits existants.
De plus, cet algorithme est compatible avec le matériel contemporain tel que les GPU, car il ne nécessite pas de formats de nombres personnalisés tels que FP4 ou les formats logarithmiques.
Cette quantification prototype + implémentation de l'opérateur INT4 MM est 2,2 fois plus rapide que la référence FP16MM et augmente la vitesse d'entraînement de 35,1 %.
Les méthodes d'entraînement entièrement quantifié (FQT) accélèrent l'entraînement en quantifiant les activations, les poids et les gradients avec une faible précision, de sorte que les opérateurs linéaires et non linéaires pendant l'entraînement peuvent être mis en œuvre en utilisant une faible précision. -arithmétique de précision.
La recherche FQT a conçu de nouveaux formats numériques et algorithmes de quantification qui peuvent mieux se rapprocher des tenseurs en pleine précision.
La frontière actuelle de la recherche est le FQT 4 bits. FQT est un défi en raison de la large plage numérique de gradients et du problème d'optimisation de la formation d'un réseau quantifié à partir de zéro.
En raison de ces défis, les algorithmes FQT 4 bits existants souffrent toujours d'une perte de précision de 1 à 2,5 % sur certaines tâches et ne peuvent pas prendre en charge le matériel contemporain.
Photos
Le mélange d'experts augmente la capacité du modèle sans augmenter le budget de formation.
Le décrochage structurel utilise des méthodes informatiques efficaces pour régulariser le modèle. Une attention efficace réduit la complexité temporelle quadratique de l’attention informatique.
Le système de formation distribué réduit le temps de formation en utilisant davantage de ressources informatiques.
Le travail des chercheurs visant à réduire la précision numérique est orthogonal à ces directions.
Photos
Propagation vers l'avant
La formation sur les réseaux neuronaux est un processus d'optimisation itératif qui calcule les gradients stochastiques par propagation vers l'avant et vers l'arrière.
L'équipe de recherche utilise un algorithme d'entier 4 bits (INT4) pour accélérer la propagation vers l'avant et vers l'arrière.
La propagation vers l'avant peut être implémentée avec une combinaison d'opérateurs linéaires et non linéaires (GeLU, normalisation, softmax, etc.).
Au cours de notre processus de formation, nous accélérons tous les opérateurs linéaires avec l'arithmétique INT4 et conservons tous les opérateurs non linéaires les moins coûteux en termes de calcul au format à virgule flottante 16 bits (FP16).
Toutes les opérations linéaires dans Transformer peuvent être écrites sous forme de multiplication matricielle (MM).
Pour faciliter l'expression, cet article considère l'accélération suivante d'une multiplication matricielle simple :
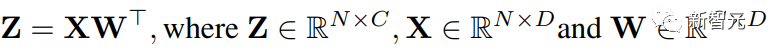Image
Le principal cas d'utilisation de ce type de MM est la couche entièrement connectée.
Considérez un transformateur dont la forme d'entrée est (taille du lot S, longueur de séquence T, dimension D).
La couche entièrement connectée peut être exprimée comme la formule ci-dessus, où X est l'activation de N = STtoken et W est la matrice de poids.
Pour la couche d'attention, une multiplication matricielle par lots (BMMS) peut être nécessaire.
La technologie que nous proposons peut être appliquée au BMMS.
Afin d'accélérer l'entraînement, des opérations entières doivent être utilisées pour calculer la propagation vers l'avant.
Les chercheurs ont utilisé Learning Step Quantizer (LSQ) à cette fin.
LSQ est une quantification statique. Son échelle de quantification ne dépend pas de la méthode d'entrée, elle est donc moins coûteuse que les méthodes de quantification dynamiques qui nécessitent de calculer dynamiquement l'échelle de quantification à chaque itération.
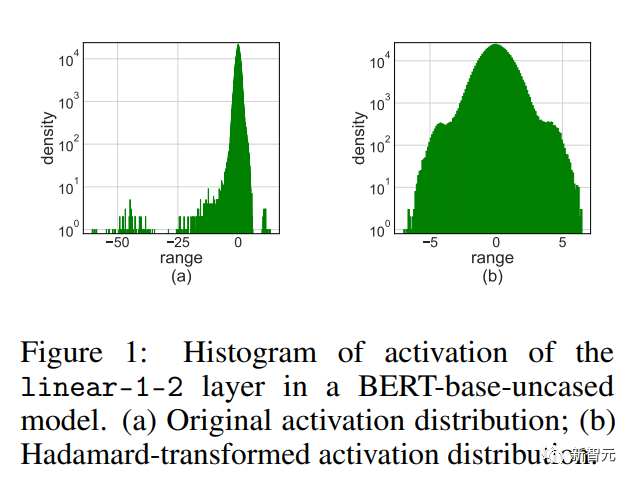
Activation des valeurs aberrantes
La simple application de LSQ à FQT avec des activations/poids de 4 bits entraînera une diminution de la précision car les valeurs aberrantes seront activées.
Image
Comme le montre l'image ci-dessus, l'activation comporte des entrées aberrantes, qui sont beaucoup plus grandes que les autres entrées.
Malheureusement, les Transformers ont tendance à stocker des informations dans ces valeurs aberrantes, et une telle troncature peut sérieusement nuire à la précision.
Le problème aberrant est particulièrement évident lorsque la tâche de formation consiste à affiner un modèle pré-entraîné sur de nouvelles tâches en aval.
Parce que le modèle pré-entraîné contient plus de valeurs aberrantes que l'initialisation aléatoire.
Nous proposons la quantification Hadamard (HQ) pour résoudre le problème des valeurs aberrantes.
L'idée principale est de quantifier une autre matrice dans un espace linéaire avec moins de valeurs aberrantes.
Les valeurs aberrantes dans la matrice d'activation forment une structure par fonctionnalités.
Ils sont généralement concentrés dans quelques dimensions, c'est-à-dire que seules quelques colonnes de X sont nettement plus grandes que les autres colonnes.
La transformée de Hardamand est une transformation linéaire qui propage les valeurs aberrantes aux autres entrées.
Rétropropagation
Nous envisageons maintenant d'utiliser les opérations INT4 pour accélérer la rétropropagation des couches linéaires.
Nous discuterons du calcul du gradient d'activation/gradient de poids dans cette section.
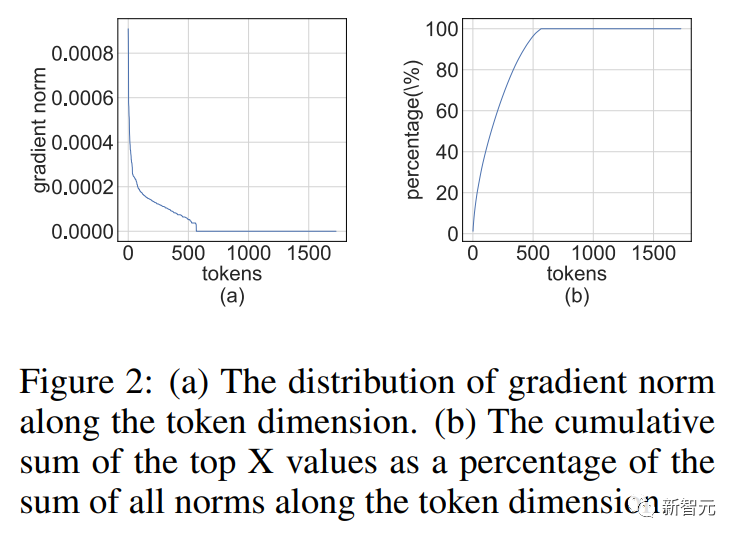
Nous avons remarqué que la matrice de gradient a tendance à être très clairsemée pendant l'entraînement.
Et la parcimonie a une telle structure : quelques lignes de
(comme les jetons) ont de grandes entrées, tandis que la plupart des autres lignes sont proches de vecteurs entièrement nuls.
Photos
Cette rareté structurelle résulte de la sévère surparamétrage des réseaux de neurones modernes.
Le réseau fonctionne selon un schéma hyperparamétré presque tout au long du processus de formation, et à l'exception de quelques exemples difficiles, il s'adapte bien à la plupart des données de formation.
Donc, pour des points de données bien ajustés, le gradient (d'activation) sera proche de zéro.
Les chercheurs ont découvert que pour les tâches de pré-formation, par exemple, la rareté structurelle apparaît rapidement après quelques époques de formation.
Pour les tâches de mise au point, le dégradé est toujours clairsemé tout au long du processus de formation.
Comment concevoir un quantificateur de gradient pour calculer avec précision le MM pendant la rétropropagation en utilisant la parcimonie structurelle ?
L'idée avancée est la suivante : de nombreuses rangées de dégradés sont si petites qu'elles ont peu d'impact sur les gradients des paramètres, mais gaspillent beaucoup de calculs.
D'un autre côté, les grandes banques ne peuvent pas être représentées avec précision par INT4.
Nous supprimons quelques petites lignes et utilisons la puissance de calcul économisée pour représenter les grandes lignes avec plus de précision.
Expériences
Les chercheurs évaluent notre algorithme de formation INT4 en le peaufinant sur une variété de tâches, notamment les modèles de langage, la traduction automatique et la classification d'images.
Les chercheurs ont utilisé CUDA et cutlass pour exécuter les algorithmes HQ-MM et LSS-MM proposés.
Les chercheurs ont remplacé tous les opérateurs linéaires à virgule flottante par des implémentations INT4, mais n'ont pas simplement utilisé LSQ pour intégrer les couches et maintenir la précision de la dernière couche de classificateur.
Enfin, les chercheurs ont adopté l'architecture, l'optimiseur, le planificateur et les hyperparamètres par défaut pour tous les modèles évalués.
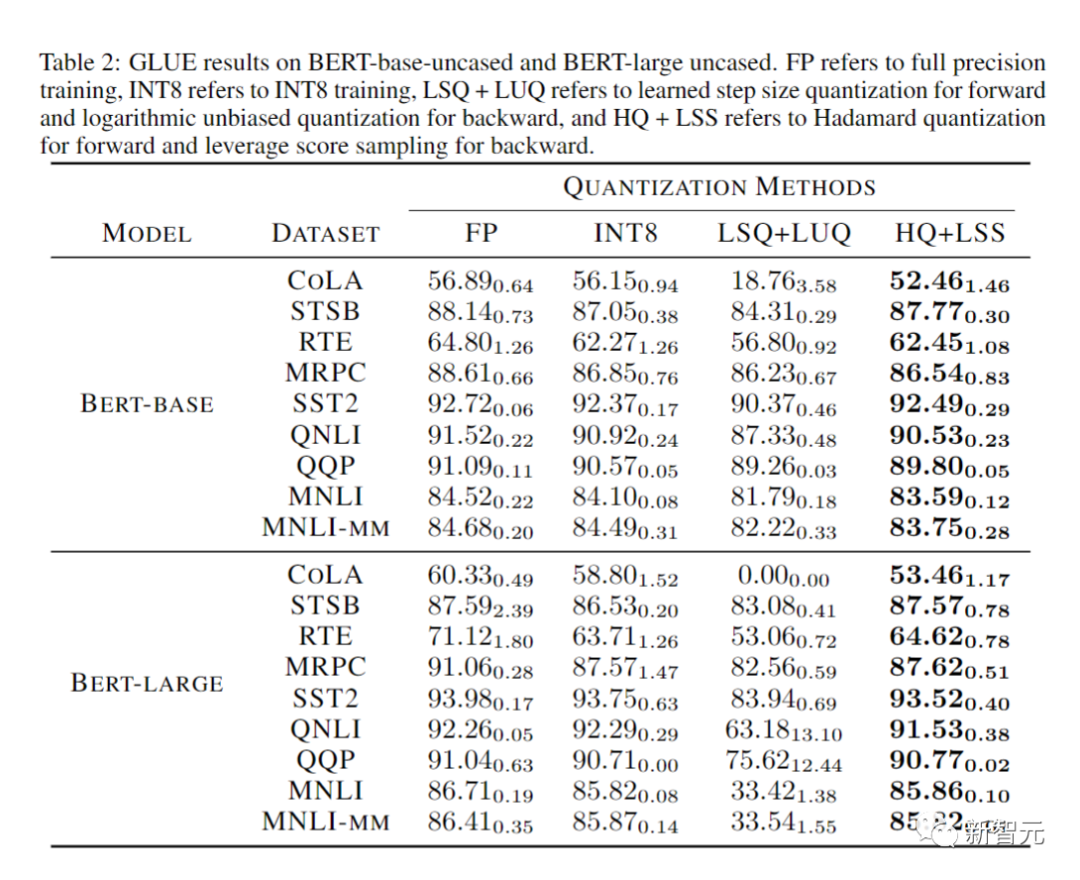
Les chercheurs ont comparé la précision des modèles convergés sur diverses tâches dans le tableau ci-dessous.
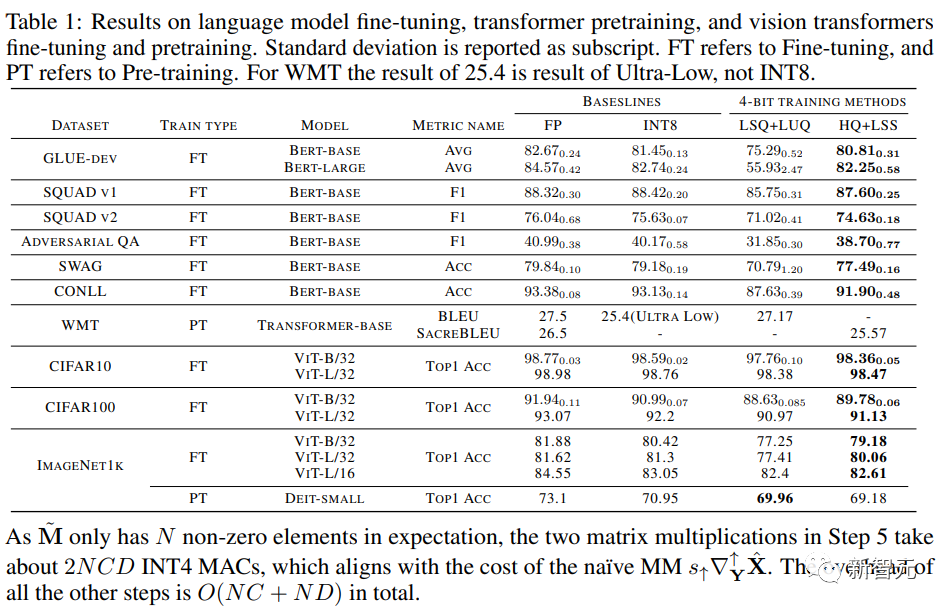Photos
À titre de comparaison, les méthodes incluent l'entraînement de précision complète (FP), l'entraînement INT8 (INT8), l'entraînement FP4 ("ultra faible"), utilisant le LSQ pour l'activation et la pondération (LSQ+LUQ) Quantification logarithmique 4 bits et notre algorithme qui utilise HQ pour la propagation vers l'avant et LSS pour la propagation arrière (HQ+LSS).
"Ultra Low" n'a pas d'implémentation publique, nous répertorions donc ses performances uniquement dans l'article original sur la tâche de traduction automatique.
À l'exception de la grande tâche de traduction automatique et de la grande tâche de transformateur visuel, nous répétons chaque exécution trois fois et rapportons l'écart type en indice dans le tableau.
Les chercheurs n’ont effectué aucun type de distillation des connaissances ou d’augmentation des données.
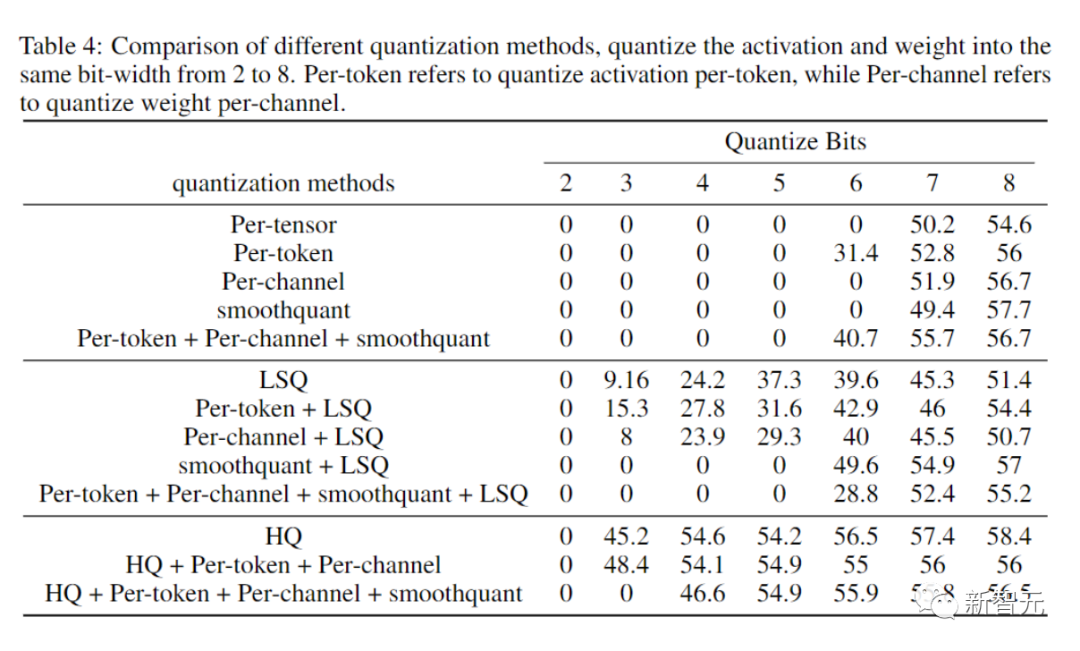
Le but de l'expérience d'ablation menée par les chercheurs était de démontrer l'efficacité des méthodes avant et arrière.
Pour étudier l'efficacité de la propagation vers l'avant pour différents quantificateurs, nous laissons la propagation vers l'arrière dans FP16.
Les résultats sont présentés dans l'image ci-dessous.
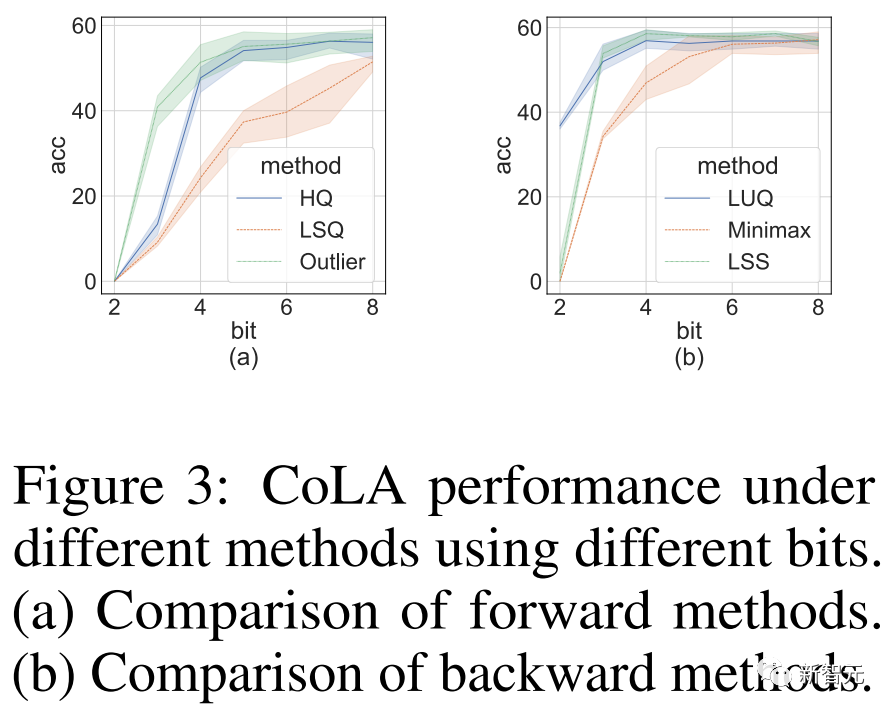Photos
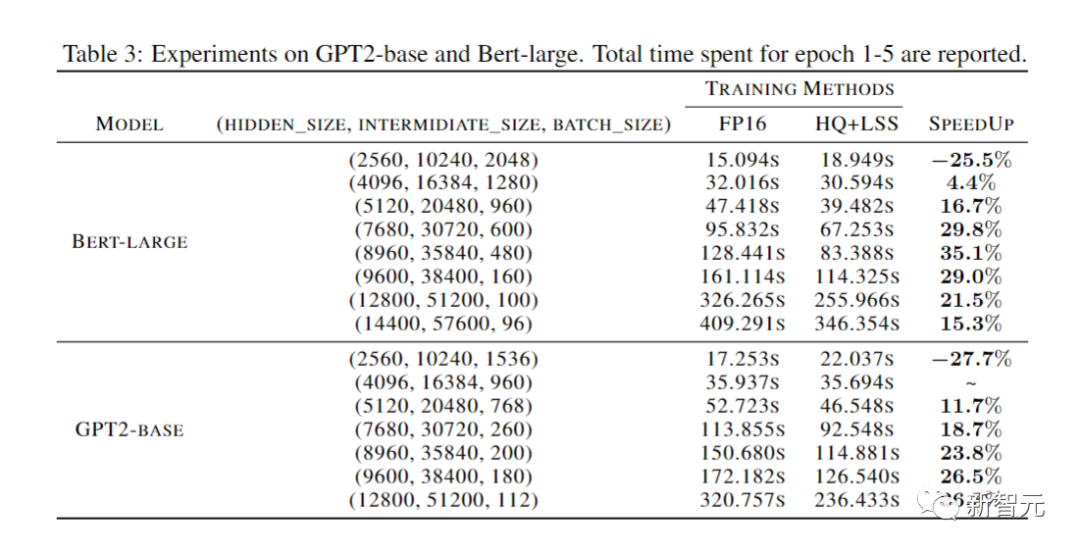
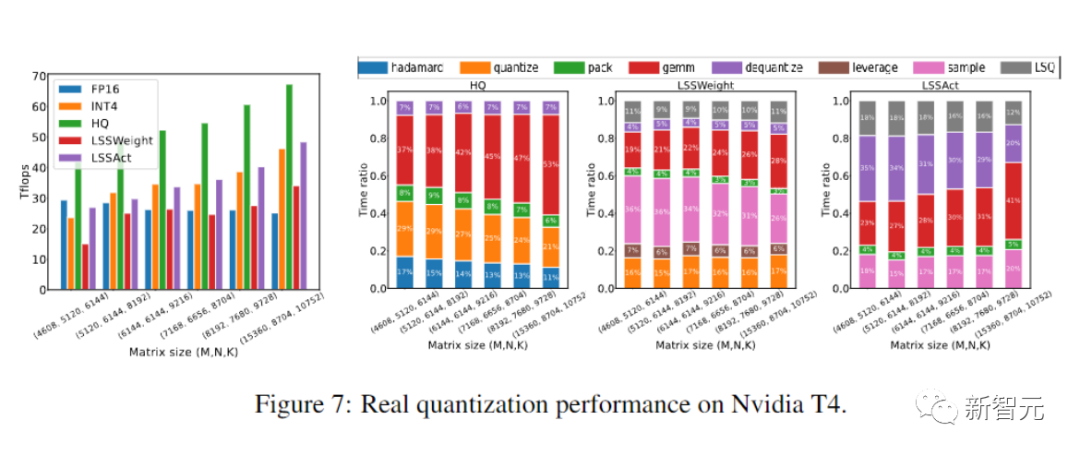
Enfin, les chercheurs ont démontré le potentiel de leur approche pour accélérer la formation des réseaux neuronaux en évaluant la mise en œuvre de leur prototype.
Et leur mise en œuvre n'est pas encore totalement optimisée.
Les chercheurs n'ont pas non plus fusionné les opérateurs linéaires avec la non-linéarité et la normalisation.
Par conséquent, les résultats ne reflètent pas pleinement le potentiel de l'algorithme d'entraînement INT4.
Une implémentation entièrement optimisée nécessite une ingénierie approfondie et dépasse le cadre de notre article.
Les chercheurs ont proposé une méthode de formation respectueuse du matériel pour Transformer INT4.
En analysant les propriétés du MM dans Transformer, les chercheurs ont proposé des méthodes HQ et LSS pour quantifier les activations et les gradients tout en maintenant la précision.
Sur plusieurs tâches importantes, notre méthode est aussi performante voire meilleure que la méthode INT4 existante.
Les travaux des chercheurs pourraient être étendus à d'autres architectures MM en plus des transformateurs, telles que MLP-Mixer, les réseaux de neurones graphiques et les réseaux de réseaux de neurones récurrents.
C'est leur future direction de recherche.
Impact plus large : L'algorithme des chercheurs peut augmenter l'efficacité et réduire la consommation d'énergie des réseaux neuronaux d'entraînement, ce qui pourrait contribuer à réduire les émissions de carbone causées par l'apprentissage en profondeur.
Cependant, des algorithmes de formation efficaces peuvent également faciliter le développement de grands modèles de langage et d'applications d'IA malveillantes qui présentent des risques pour la sécurité humaine.
Par exemple, les modèles et applications associés qui seront utilisés pour la génération de faux contenus.
Limitations : La principale limitation de ce travail est qu'il ne peut accélérer que de grands modèles avec des multiplications matricielles à plus grande échelle (couches linéaires), mais pas des couches convolutives.
De plus, la méthode proposée n'est pas bien applicable aux très gros modèles tels que l'OPT-175B.
À notre connaissance, même la formation INT8 reste un problème non résolu pour ces très gros modèles.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
