
En HTML5, l'objet CanvasRenderingContext2D fournit également des méthodes spécifiquement pour dessiner des cercles ou des arcs. Veuillez vous référer aux attributs suivants et à l'introduction de la méthode :
.Dessinez un arc sur un cercle avec le point de coordonnées (x, y) comme centre et le rayon comme rayon sur la toile. L'arc de départ de cet arc est startRad et l'arc de fin est endRad. Le radian est ici calculé comme l'angle de rotation dans le sens des aiguilles d'une montre en fonction de la direction positive de l'axe des x (trois heures de l'horloge). Dans le sens inverse des aiguilles d'une montre, indique s'il faut commencer à dessiner dans le sens inverse des aiguilles d'une montre ou dans le sens des aiguilles d'une montre. Si c'est vrai, cela signifie dans le sens inverse des aiguilles d'une montre, et si c'est faux, cela signifie dans le sens des aiguilles d'une montre. Le paramètre antihoraire est facultatif et sa valeur par défaut est false, ce qui signifie dans le sens des aiguilles d'une montre. 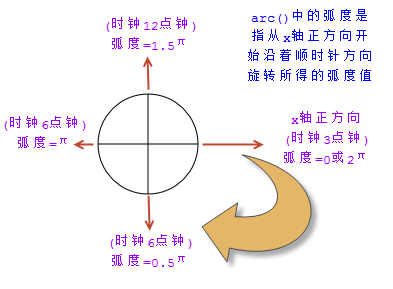
Méthode de calcul des radians dans la méthode arc()
Cette méthode utilisera l'angle formé par le point final actuel, le point final 1 (x1, y1) et le point final 2 (x2, y2), puis dessinera une section tangente aux deux côtés de l'angle et ayant un rayon de rayon Un arc sur un cercle. De manière générale, la position de départ du tracé d'un arc est le point final actuel, la position finale est le point final 2 et la direction du tracé de l'arc est la direction de l'arc le plus court reliant les deux points terminaux. De plus, si le point final actuel ne se trouve pas sur le cercle spécifié, cette méthode tracera également une ligne droite depuis le point final actuel jusqu'au point de départ de l'arc.
Comme il y a beaucoup d'espace pour présenter la méthode arcTo() en détail, veuillez cliquer ici pour voir l'utilisation détaillée d'arcTo().
Après avoir compris l'API ci-dessus pour dessiner des arcs sur un canevas, voyons comment utiliser arc() pour dessiner des arcs. Nous savons déjà que les 4ème et 5ème paramètres reçus par arc() représentent les radians de début et de fin de l'arc. Je crois que tous les lecteurs ont appris le radian dans les cours de mathématiques ou de géométrie à l'école. Le radian est une unité d'angle. Pour un arc dont la longueur d’arc est égale à son rayon, l’angle au centre qu’il sous-tend est de 1 radian. On sait aussi qu'un cercle de rayon r a une circonférence 2πr. Avec cette connaissance de la géométrie, nous pouvons utiliser la méthode arc() pour dessiner des arcs.
Utilisez la toile pour dessiner des arcs
Maintenant, dessinons un 1/4 d'arc de cercle avec un rayon de 50px.
L'effet d'affichage correspondant est le suivant : 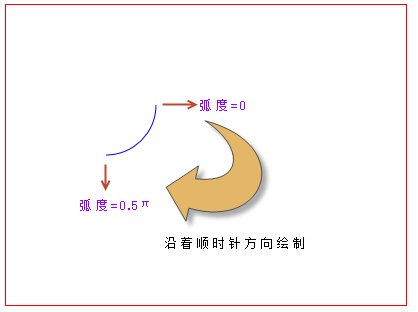
Utilisez le canevas pour dessiner un arc dans le sens des aiguilles d'une montre
Comme indiqué ci-dessus, nous définissons les coordonnées centrales du cercle où se trouve l'arc dessiné sur (100,100) et le rayon sur 50px. Puisque la circonférence d'un cercle de rayon r est 2πr, c'est-à-dire que le radian correspondant d'un cercle complet est 2π (converti en un angle régulier est de 360°), nous voulons donc dessiner 1/4 de l'arc de cercle, tant que le radian est π/2 (soit 90°). Dans le code ci-dessus, nous utilisons la constante Math.PI qui représente π en JavaScript.
De plus, dans le code ci-dessus, nous définissons également la direction de dessin des arcs dans le sens des aiguilles d'une montre (faux). Puisque le radian de départ est 0 et le radian de fin est π/2, l'arc sera tracé dans le sens des aiguilles d'une montre en partant de la direction positive de l'axe des x, ce qui donnera le graphique ci-dessus. Si nous changeons la direction de dessin de l’arc dans le code ci-dessus dans le sens inverse des aiguilles d’une montre, quel sera l’effet ?
L'effet d'affichage correspondant est le suivant : 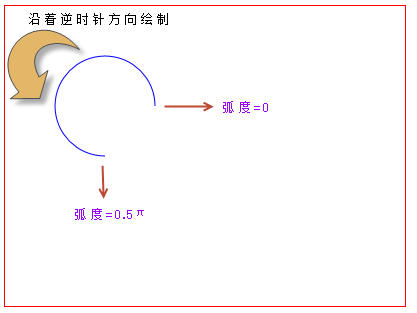
Utilisez le canevas pour dessiner un arc dans le sens inverse des aiguilles d'une montre
Utilisez une toile pour dessiner un cercle
Après avoir appris à dessiner des arcs, il est facile de dessiner des cercles par analogie. Il suffit de changer l'arc final du code ci-dessus en 2π.
 Quelles sont les méthodes de production de production d'animation html5 ?
Quelles sont les méthodes de production de production d'animation html5 ?
 La différence entre HTML et HTML5
La différence entre HTML et HTML5
 Introduction à l'utilisation du code complet VBS
Introduction à l'utilisation du code complet VBS
 Qu'est-ce qu'une connexion directe indépendante ?
Qu'est-ce qu'une connexion directe indépendante ?
 Collection de codes d'images HTML
Collection de codes d'images HTML
 Que fait Matcha Exchange ?
Que fait Matcha Exchange ?
 Que signifie DHCP ?
Que signifie DHCP ?
 Que faire si le post-scriptum ne peut pas être analysé
Que faire si le post-scriptum ne peut pas être analysé