
Les modèles de langage à grande échelle tels que GPT et PaLM sont de plus en plus aptes à gérer des tâches telles que le raisonnement mathématique, symbolique, de bon sens et de connaissances. Il est peut-être surprenant que la base de toutes ces avancées reste le mécanisme autorégressif original de génération de texte. Il prend des décisions jeton par jeton et génère du texte de gauche à droite. Un mécanisme aussi simple est-il suffisant pour construire un modèle de langage destiné à résoudre un problème général ? Dans la négative, quels problèmes remettront en question le paradigme actuel et quels mécanismes alternatifs devraient être utilisés ?
La littérature sur la cognition humaine fournit quelques indices pour répondre à ces questions. La recherche sur le modèle du « double processus » montre que les gens ont deux modes de prise de décision : l'un est un mode rapide, automatique et inconscient (Système 1), et l'autre est un mode lent, délibéré et conscient (Système 2). . Ces deux modèles ont déjà été associés à divers modèles mathématiques utilisés en apprentissage automatique. Par exemple, la recherche sur l’apprentissage par renforcement chez les humains et d’autres animaux explore s’ils s’engagent dans un apprentissage associatif « sans modèle » ou dans une planification plus délibérée « basée sur un modèle ». La sélection associative simple au niveau du jeton des modèles de langage est également similaire au « Système 1 » et peut donc bénéficier de l'amélioration d'un processus de planification plus réfléchi du « Système 2 » qui maintient et explore plusieurs alternatives à la sélection actuelle, pas seulement en choisir une. . De plus, il évalue son état actuel et regarde activement vers l’avenir ou vers le passé pour prendre des décisions plus globales.
Afin de concevoir un tel processus de planification, des chercheurs de l'Université de Princeton et de Google DeepMind ont choisi de revenir d'abord sur les origines de l'intelligence artificielle (et des sciences cognitives) et de tirer les leçons du processus de planification exploré par Newell, Shaw et Simon dans les inspirations des années 1950. Newell et ses collègues décrivent la résolution de problèmes comme la recherche d'un espace de problèmes combinatoire représenté par un arbre. Par conséquent, ils ont proposé un cadre d’arbre de pensée (ToT) adapté aux modèles de langage pour la résolution générale de problèmes.

Lien papier : https://arxiv.org/pdf/2305.10601.pdf
Adresse du projet : https://github.com/ysymyth/tree-of -thought-llm
Comme le montre la figure 1, les méthodes existantes résolvent le problème en échantillonnant des séquences linguistiques continues, tandis que ToT maintient activement un arbre de pensée dans lequel chaque pensée est une séquence linguistique cohérente comme étapes intermédiaires dans la résolution de problèmes (tableau 1).
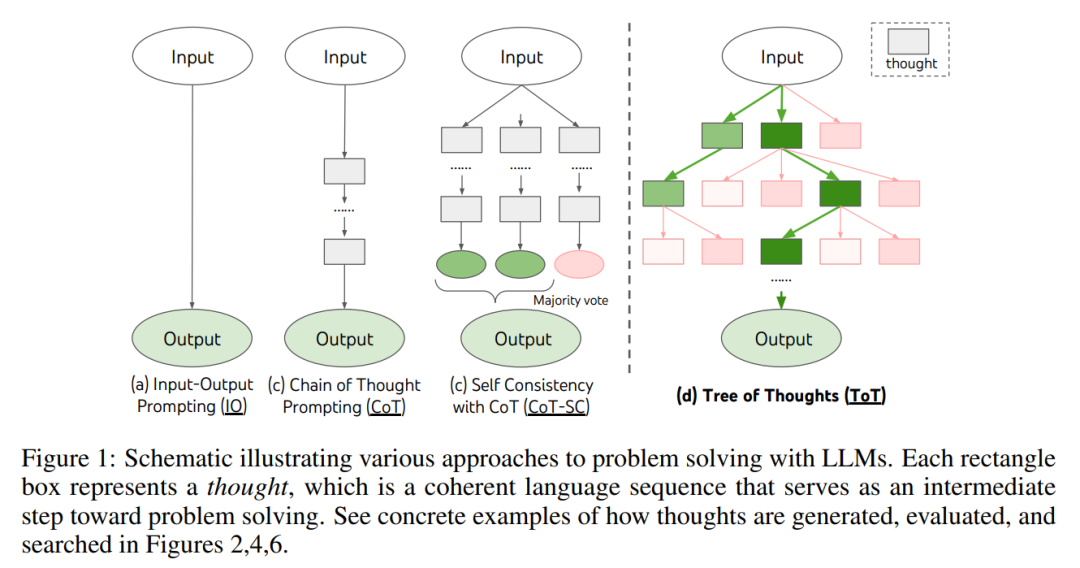

Une telle unité sémantique de haut niveau permet à LM d'auto-évaluer la contribution de différentes pensées intermédiaires à la progression de la résolution de problèmes grâce à un processus de raisonnement réfléchi (Figures 2, 4, 6) . La mise en œuvre d'heuristiques de recherche par le biais de l'auto-évaluation et de la délibération du LM est une approche nouvelle, car les heuristiques de recherche précédentes étaient soit programmées, soit apprises.


Enfin, les chercheurs ont combiné cette capacité basée sur le langage à générer et à évaluer diverses pensées avec des algorithmes de recherche tels que la recherche en largeur (BFS) ou la recherche en profondeur (DFS). ), ces algorithmes permettent une exploration systématique des arbres de pensée, avec des capacités d'anticipation et de retour en arrière.
Dans la phase expérimentale, les chercheurs ont défini trois tâches, à savoir le jeu en 24 points, l'écriture créative et les mots croisés (tableau 1). Ces problèmes sont assez difficiles pour les méthodes d'inférence LM existantes, même pour GPT-4 ne fait pas exception. Ces tâches nécessitent des connaissances déductives, mathématiques, générales, des compétences de raisonnement lexical et un moyen d'intégrer une planification ou une recherche systématique. Les résultats expérimentaux montrent que ToT obtient des résultats supérieurs sur ces trois tâches car il est suffisamment polyvalent et flexible pour prendre en charge différents niveaux de réflexion, différentes manières de générer et d'évaluer la réflexion, et s'adapte à différentes natures de problèmes. Grâce à une analyse expérimentale systématique de l'ablation, les auteurs explorent également comment ces choix affectent les performances du modèle et discutent des orientations futures en matière de formation et d'utilisation des LM.
Un véritable processus de résolution de problèmes implique l'utilisation itérative des informations disponibles pour lancer l'exploration, qui à son tour révèle plus d'informations, jusqu'à ce qu'un moyen de parvenir à une solution soit finalement découvert. ——Newell et al.
La recherche sur la résolution de problèmes humains montre que les humains résolvent les problèmes en recherchant un espace de problèmes combinatoire. Cela peut être vu comme un arbre, où les nœuds représentent des solutions partielles et les branches correspondent aux opérateurs qui les modifient. La branche choisie est déterminée par des heuristiques qui aident à naviguer dans l’espace du problème et guident la personne qui résout le problème vers la solution. Cette perspective met en évidence deux principales lacunes des approches existantes qui utilisent des modèles de langage pour résoudre des problèmes généraux : 1) Localement, elles n'explorent pas les différentes suites du processus de pensée – les branches de l'arbre. 2) Globalement, elles n’incluent aucune sorte de planification, d’anticipation ou de retour en arrière pour aider à évaluer ces différentes options – le genre de recherche guidée par des heuristiques qui semble caractériser la résolution de problèmes humains.
Pour résoudre ces problèmes, l'auteur présente l'Arbre de Pensée (ToT), un paradigme qui permet aux modèles de langage d'explorer plusieurs méthodes de raisonnement sur le chemin de la pensée (Figure 1 (c)). ToT présente tout problème comme une recherche d'un arbre, où chaque nœud est un état s = [x, z_1・・・i ], représentant une solution partielle avec entrée et une séquence de pensées jusqu'à présent. Des exemples spécifiques de ToT incluent la réponse aux quatre questions suivantes :
2. Générateur de pensées G (p_θ, s, k). Étant donné un état d'arbre s = [x, z_1・・・i], cette étude utilise deux stratégies pour générer k candidats pour la prochaine étape de réflexion.
3. Évaluateur d'état V (p_θ, S). Compte tenu des frontières des différents États, l’évaluateur d’État évalue leurs progrès vers la résolution du problème afin de déterminer quels États doivent continuer à être explorés et dans quel ordre. Bien que les heuristiques soient un moyen standard de résoudre les problèmes de recherche, elles sont souvent soit programmatiques (par exemple DeepBlue), soit apprises (par exemple AlphaGo). Cet article propose une troisième alternative, consistant à utiliser le langage pour raisonner intentionnellement sur les États. Le cas échéant, ces heuristiques réfléchies peuvent être plus flexibles que les règles de programmation et plus efficaces que les modèles d’apprentissage.
Semblable au générateur de pensées, envisagez deux stratégies pour évaluer les états individuellement ou ensemble :
(1) Évaluez chaque état indépendamment
4. Algorithme de recherche. Enfin, dans le cadre ToT, il est possible de brancher et de jouer différents algorithmes de recherche basés sur la structure arborescente. Cet article explore deux algorithmes de recherche relativement simples et laisse des algorithmes plus avancés pour des recherches futures :
Conceptuellement, ToT présente plusieurs avantages en tant que méthode permettant aux modèles de langage de résoudre des problèmes généraux :
L'étude présente trois tâches qui restent difficiles même en utilisant le modèle de langage de pointe GPT-4, échantillonnées via une invite d'E/S standard ou une invite de chaîne de pensée (CoT).
Jeu mathématique en 24 points
Étant donné quatre nombres, les joueurs doivent utiliser ces quatre nombres et les symboles d'opérations mathématiques de base (signe plus, signe moins, signe de multiplication, signe de division) dans un temps limité pour créer un expression qui vaut 24. Par exemple, étant donné les nombres : 4, 6, 8, 2, une solution possible est : (8 ÷ (4 - 2)) × 6 = 24.
Comme le montre le tableau 2, l'utilisation des méthodes d'invite IO, CoT et CoT-SC a donné de mauvais résultats sur la tâche, atteignant seulement 7,3 %, 4,0 % et 9,0 % de taux de réussite. En comparaison, ToT avec b(breadth) = 1 a atteint un taux de réussite de 45 %, et avec b = 5 il atteint 74 %. Ils ont également pris en compte le paramètre Oracle d'IO/CoT pour calculer le taux de réussite en utilisant la meilleure valeur parmi k échantillons (1 ≤ k ≤ 100).
Pour comparer IO/CoT (k meilleurs résultats) avec ToT, le chercheur envisage de compter le nombre de nœuds d'arbre visités dans chaque tâche dans ToT, où b = 1・・・5, et 5. Les taux de réussite sont cartographiés dans Figure 3 (a), considérant l'IO/CoT (k meilleurs résultats) comme la visite de k nœuds dans une machine à sous. Sans surprise, CoT est plus évolutif que IO, et les 100 meilleurs échantillons CoT ont atteint un taux de réussite de 49 %, ce qui est encore bien inférieur à l'exploration de plus de nœuds dans ToT (b > 1).

La figure 3 (b) ci-dessous décompose les échantillons CoT et ToT lorsque la tâche échoue. Notamment, environ 60 % des échantillons CoT ont déjà échoué après la première étape de génération, équivalente à la génération des trois premiers mots (par exemple « 4 + 9 »). Cela rend le problème du décodage direct de gauche à droite encore plus évident.

Écriture créative
Les chercheurs ont également inventé une tâche d'écriture créative, saisissant 4 phrases aléatoires et produisant un article cohérent contenant quatre paragraphes, chaque paragraphe commençant par 4. phrase d’entrée. Ces tâches sont ouvertes et exploratoires, mettant au défi la pensée créative et la planification de haut niveau.
La figure 5 (a) ci-dessous montre le score moyen de GPT-4 sur 100 tâches, où ToT (7,56) génère des paragraphes plus cohérents que IO (6,19) et CoT (6,93). Bien que de telles mesures automatiques puissent être bruyantes, la figure 5 (b) confirme que les humains préfèrent ToT à CoT dans 41 paires de passages sur 100, tandis que seulement 21 paires préfèrent CoT à ToT (les 38 autres paires ont été jugées « tout aussi cohérentes »).
Enfin, l'algorithme d'optimisation itératif a obtenu de meilleurs résultats sur cette tâche en langage naturel, avec le score de cohérence IO augmentant de 6,19 à 7,67 et le score de cohérence ToT passant de 7,56 à 7,91. Les chercheurs pensent que cela peut être considéré comme la troisième méthode de génération de pensée dans le cadre ToT. Une nouvelle pensée peut être générée à partir du raffinement de l'ancienne pensée plutôt que de la génération séquentielle.

Mini mots croisés
Dans "24 Dot Math Game" et l'écriture créative, ToT est relativement simple - il faut jusqu'à 3 étapes de réflexion pour atteindre le résultat final. Les chercheurs exploreront les mini-mots croisés 5×5 comme une couche plus difficile de questions de recherche sur le langage naturel. Encore une fois, l’objectif cette fois n’est pas seulement de résoudre la tâche, car les mots croisés généraux peuvent être facilement résolus par un pipeline PNL spécialisé qui exploite la récupération à grande échelle au lieu du LM. Au lieu de cela, les chercheurs visent à explorer les limites d’un modèle de langage en tant que solution générale à un problème, à explorer sa propre pensée et à utiliser un raisonnement rigoureux comme heuristique pour guider son exploration.
Comme le montre le tableau 3 ci-dessous, les méthodes d'invite IO et CoT fonctionnent mal, avec des taux de réussite au niveau des mots inférieurs à 16 %, tandis que ToT améliore considérablement toutes les mesures, atteignant un taux de réussite au niveau des mots de 60 %, en 20 4. résolu dans le jeu. Cette amélioration n’est pas surprenante étant donné que l’IO et le CoT manquent de mécanismes pour essayer différents signaux, modifier les décisions ou revenir en arrière.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!