
Le tri Hill, également appelé « tri réducteur incrémentiel », est un algorithme de tri produit en optimisant le tri par insertion. Son idée d'exécution est la suivante : regrouper les éléments du tableau en incréments d'indice, insérer et trier chaque groupe d'éléments, réduire l'incrément et répéter les étapes précédentes jusqu'à ce que l'incrément atteigne 1.
D'une manière générale, la complexité temporelle du tri Hill est O(n1.3)~O(n2), qui dépend de la taille de l'incrément. La complexité spatiale du tri Hill est O(1), qui est un algorithme de tri instable. Lors du tri Hill, un mouvement d'un élément peut s'étendre sur plusieurs éléments, ce qui peut compenser plusieurs mouvements et améliorer l'efficacité.
Ce qui suit est un tri Hill ascendant utilisant (longueur du tableau/2) comme incrément initial. Après chaque tour de tri, l'incrément est réduit de moitié.
Comme le montre la figure 2-28, en commençant par le premier élément, regroupez par incrément de 4. On peut voir que lorsque l'incrément est de 4, il n'y a que deux éléments dans un groupe, sinon l'indice de l'élément dépassera la plage du tableau.
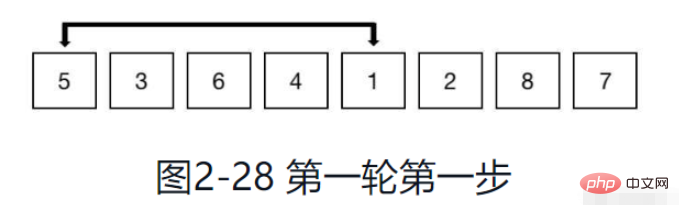
Comme le montre la figure 2-29, effectuez un tri par insertion sur les éléments du groupe.
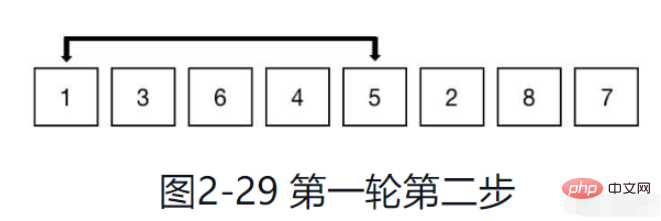
Comme le montre la figure 2-30, continuez à utiliser la même méthode pour regrouper et effectuez un tri par insertion sur les éléments du groupe pour les rendre ordonnés.
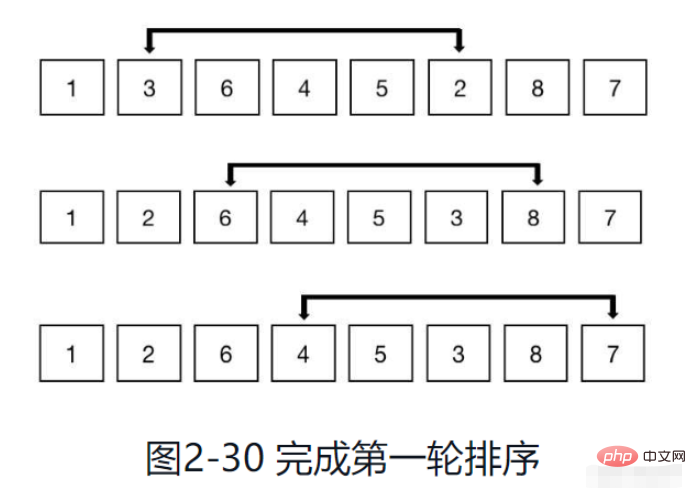
Une fois que tous les nombres de l'ensemble du tableau ont été parcourus, ce tour de tri est terminé. Réduisez l’incrément de moitié et continuez avec le prochain tour de tri.
Comme le montre la figure 2-31, lorsque l'incrément est de 2, on peut voir que les éléments de chaque groupe ont augmenté et que le nombre total de groupes a diminué. Continuez le tri par insertion des éléments dans chaque groupe jusqu'à ce que chaque groupe soit parcouru.
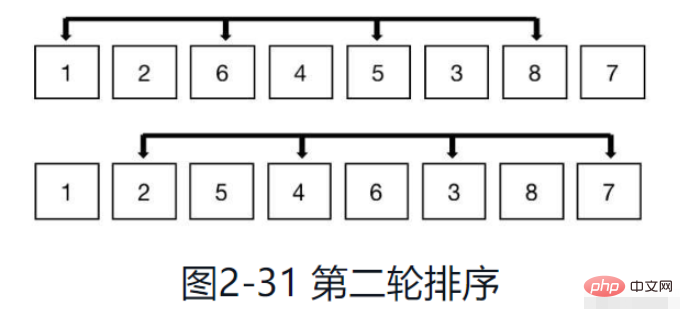
Le dernier tour de tri est illustré dans la figure 2-32. Réduisez à nouveau l'incrément de moitié à ce moment, l'incrément est de 1, ce qui équivaut au tri par insertion de l'ensemble du tableau, c'est-à-dire le tri du dernier tour.
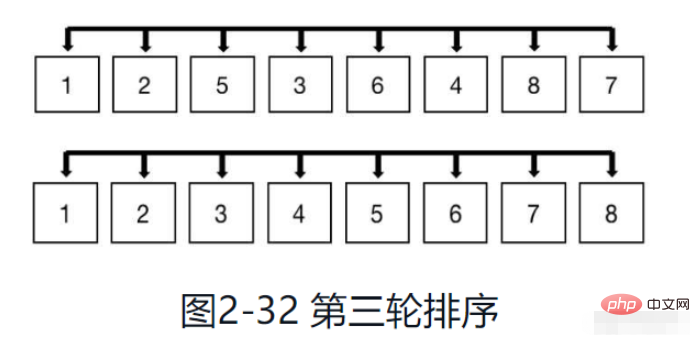
Après le dernier tour de tri, tout le tri Hill est terminé.
Dans la boucle for, puisque le premier élément de chaque groupe n'a pas besoin d'être inséré et trié et que leurs indices sont compris entre 0 et l'étape 1, le parcours commence à partir de l'étape d'indice.
Il est à noter que si vous souhaitez simuler l'approche dans l'organigramme, vous devez utiliser deux boucles : d'abord regrouper, puis ordonner les éléments d'un même groupe en une seule fois. Afin d'améliorer l'efficacité, nous utilisons directement une boucle for, et chaque fois qu'un nombre est parcouru, le groupe dans lequel il se trouve est inséré et trié. Ce parcours répond également aux exigences d’ordre du tri par insertion. Dans le tri par insertion, la valeur de l'indice actuel doit être modifiée, donc la variable ind est utilisée pour stocker l'indice actuel afin d'éviter qu'il n'affecte la boucle for.
Le tri par insertion ordinaire est équivalent au tri Hill avec un incrément de 1. Le tri Hill entre les éléments ne modifie en fait que l'incrément et n'est logiquement pas différent du tri par insertion ordinaire.
Code de tri des collines :
nums = [5,3,6,4,1,2,8,7]
def ShellSort(nums):
step = len(nums)//2 #初始化增量为数组长度的一半
while step > 0: #增量必须是大于0的整数
for i in range(step,len(nums)): #遍历需要进行插入排序的数
ind = i
while ind >= step and nums[ind] < nums[ind-step]: #对每组进行插入排序
nums[ind],nums[ind-step] = nums[ind-step],nums[ind]
ind -= step
step //= 2 #增量缩小一半
print(nums)
ShellSort(nums)Exécutez le programme, le résultat de sortie est :
[1,2,3,4,5,6,7,8]
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!