Un article discute brièvement de la capacité de généralisation du deep learning

1. La question de la capacité de généralisation du DNN

L'article explique principalement pourquoi le modèle de réseau neuronal surparamétré peut avoir de bonnes performances de généralisation ? Autrement dit, il ne mémorise pas simplement l'ensemble de formation, mais résume une règle générale de l'ensemble de formation, afin qu'elle puisse être adaptée à l'ensemble de test (capacité de généralisation).

Prenons l'exemple du modèle d'arbre de décision classique. Lorsque le modèle d'arbre apprend les règles générales de l'ensemble de données : une bonne situation est que si l'arbre divise d'abord le nœud, il peut simplement bien distinguer les échantillons avec des étiquettes différentes. . , la profondeur est très faible et le nombre correspondant d'échantillons sur chaque feuille est suffisant (c'est-à-dire que la quantité de données basées sur des règles statistiques est également relativement importante), alors les règles obtenues sont plus susceptibles d'être généralisées à d'autres données. . (c'est-à-dire : bon ajustement et capacité de généralisation).

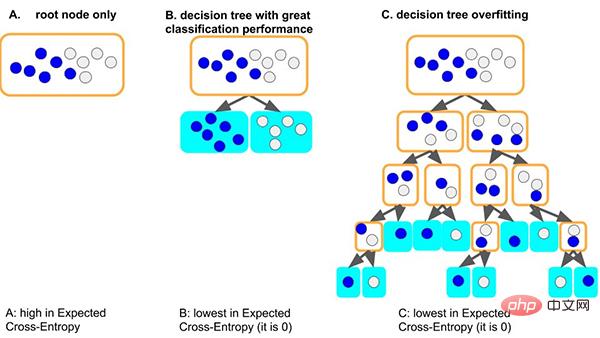
Une autre situation pire est que si l'arbre ne peut pas apprendre certaines règles générales, afin d'apprendre cet ensemble de données, l'arbre deviendra de plus en plus profond, et chaque nœud feuille peut correspondre à un petit nombre d'échantillons (moins le les informations statistiques apportées par les données peuvent n'être que du bruit), et enfin, mémoriser toutes les données par cœur (c'est-à-dire : surapprentissage et aucune capacité de généralisation). Nous pouvons voir que les modèles d’arbres trop profonds peuvent facilement être surajustés.

Alors, comment un réseau de neurones surparamétré peut-il parvenir à une bonne généralisation ?

2. Les raisons de la capacité de généralisation du DNN

Cet article explique d'un point de vue simple et général - en explorant les raisons de la capacité de généralisation dans le processus d'optimisation de la descente de gradient des réseaux de neurones :

Nous avons résumé la théorie de la cohérence du gradient : Les gradients des différents échantillons produisent de la cohérence, c'est pourquoi les réseaux de neurones peuvent avoir de bonnes capacités de généralisation. Lorsque les gradients des différents échantillons sont bien alignés pendant l’entraînement, c’est-à-dire lorsqu’ils sont cohérents, la descente de gradient est stable, peut converger rapidement et le modèle résultant peut bien se généraliser. Sinon, si les échantillons sont trop peu nombreux ou si le temps de formation est trop long, cela risque de ne pas se généraliser.

Sur la base de cette théorie, nous pouvons faire l'explication suivante.

2.1 Généralisation des réseaux de neurones de largeur

Les modèles de réseaux de neurones plus larges ont de bonnes capacités de généralisation. En effet, les réseaux plus larges comportent plus de sous-réseaux et sont plus susceptibles de produire une cohérence de gradient que les réseaux plus petits, ce qui entraîne une meilleure généralisation. En d’autres termes, la descente de gradient est un sélecteur de fonctionnalités qui donne la priorité aux gradients de généralisation (cohérence), et des réseaux plus larges peuvent avoir de meilleures fonctionnalités simplement parce qu’ils ont plus de fonctionnalités.

• Article original : Généralisation et largeur. Neyshabur et al. [2018b] ont découvert que les réseaux plus larges se généralisent mieux. Pouvons-nous maintenant expliquer cela de manière intuitive, les réseaux plus larges ont plus de sous-réseaux à un niveau donné, et donc le sous-réseau. avec une cohérence maximale dans un réseau plus large peut être plus cohérent que son homologue dans un réseau plus mince, et donc mieux généraliser. En d'autres termes, puisque - comme discuté dans la section 10 - la descente de gradient est un sélecteur de fonctionnalités qui donne la priorité à une bonne généralisation (cohérente). En termes de fonctionnalités, les réseaux plus larges sont susceptibles d'avoir de meilleures fonctionnalités simplement parce qu'ils ont plus de fonctionnalités. À cet égard, voir également l'hypothèse des billets de loterie [Frankle et Carbin, 2018]
• Lien papier : https://github.com/aialgorithm/Blog.

Mais personnellement, je pense qu'il faut encore distinguer la largeur de la couche d'entrée réseau/couche cachée. Surtout pour la couche d'entrée des tâches d'exploration de données, étant donné que les entités d'entrée sont généralement conçues manuellement, vous devez envisager la sélection des entités (c'est-à-dire réduire la largeur de la couche d'entrée, sinon l'entrée directe du bruit des entités interférera avec la cohérence du dégradé). .

2.2 Généralisation des réseaux de neurones profonds

Plus le réseau est profond, le phénomène de cohérence du gradient est amplifié et a une meilleure capacité de généralisation.

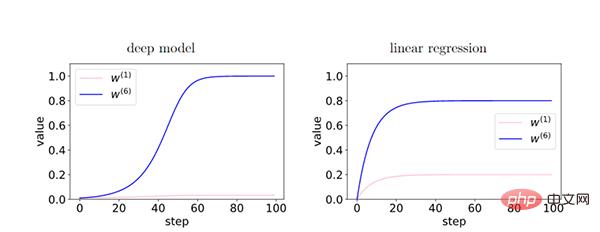
Dans le modèle profond, puisque le feedback entre les couches renforce le gradient cohérent, il existe une différence relative entre les caractéristiques du gradient cohérent (W6) et les caractéristiques du gradient incohérent (W1) pendant le processus d'entraînement. De manière exponentielle amplifié. Cela amène les réseaux plus profonds à préférer les gradients cohérents, ce qui se traduit par de meilleures capacités de généralisation.

2.3 Arrêt anticipé

En arrêtant tôt, nous pouvons réduire l'influence excessive des gradients incohérents et améliorer la généralisation.

Pendant l'entraînement, certains échantillons faciles s'ajustent plus tôt que d'autres échantillons (échantillons durs). Au début de la formation, le gradient de corrélation de ces échantillons faciles domine et est facile à ajuster. Au stade ultérieur de la formation, le gradient incohérent des échantillons difficiles domine le gradient moyen g(wt), ce qui entraîne une faible capacité de généralisation. À ce stade, il est nécessaire de s'arrêter tôt.

• (Remarque : les échantillons simples sont ceux qui ont de nombreux gradients en commun dans l'ensemble de données. Pour cette raison, la plupart des gradients lui sont bénéfiques et convergent plus rapidement.)

2.4 Descente de gradient complet VS taux d'apprentissage

Nous avons constaté que la descente à gradient complet peut également avoir une bonne capacité de généralisation. En outre, des expériences minutieuses montrent que la descente de gradient stochastique ne conduit pas nécessairement à une meilleure généralisation, mais cela n'exclut pas la possibilité que les gradients stochastiques soient plus susceptibles de sortir des minima locaux, de jouer un rôle dans la régularisation, etc.

• Sur la base de notre théorie, le taux d'apprentissage fini et la stochasticité des mini-lots ne sont pas nécessaires pour la généralisation

Nous pensons qu'un taux d'apprentissage inférieur ne peut pas réduire l'erreur de généralisation, car un taux d'apprentissage inférieur signifie plus de nombre d'itérations (à l'opposé d'arrêt anticipé).

• En supposant un taux d'apprentissage suffisamment faible, à mesure que la formation progresse, l'écart de généralisation ne peut pas diminuer. Cela découle de l'analyse itérative de la stabilité de la formation : avec 40 étapes supplémentaires, la stabilité ne peut que se dégrader. indiquerait une limitation intéressante de la théorie

2.5 Régularisation L2 et L1

Ajoutez la régularisation L2 et L1 à la fonction objectif, et le calcul du gradient correspondant, le gradient qui doit être ajouté au terme de régularisation L1 est le signe ( w), et le gradient L2 est w. En prenant la régularisation L2 comme exemple, la formule de mise à jour du gradient W(i+1) correspondante est : Image

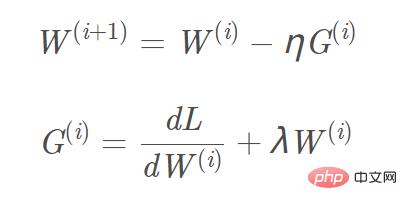
Nous pouvons considérer la « régularisation L2 (atténuation du poids) » comme une « force de fond », et chaque paramètre est poussé proche d'une valeur zéro indépendante des données (L1 est facile d'obtenir une solution clairsemée, et L2 est facile d'obtenir une solution lisse proche de 0) pour éliminer l'influence dans la direction du gradient faible. Ce n'est que dans le cas de directions de gradient cohérentes que les paramètres peuvent être relativement séparés de la « force de fond » et que la mise à jour du gradient peut être effectuée sur la base des données.

2.6 Avancement de l'algorithme de descente de gradient

• Momentum, Adam et autres algorithmes de descente de gradient

Momentum, Adam et autres algorithmes de descente de gradient, la direction de mise à jour du paramètre W est non seulement déterminée par le gradient actuel, mais également par le gradient précédemment accumulé. La direction du gradient est liée (c'est-à-dire que l'effet des gradients cohérents accumulés est préservé). Cela permet aux paramètres d'être mis à jour plus rapidement dans les dimensions où la direction du gradient change légèrement, et réduit l'amplitude de mise à jour dans les dimensions où la direction du gradient change de manière significative, ce qui a pour effet d'accélérer la convergence et de réduire l'oscillation.

• Supprimer la descente de gradient dans les directions de gradient faible

Nous pouvons supprimer les mises à jour de gradient dans les directions de gradient faible en optimisant l'algorithme de descente de gradient par lots, améliorant ainsi les capacités de généralisation. Par exemple, nous pouvons utiliser la descente de gradient winsorisée pour exclure les valeurs aberrantes du gradient, puis prendre la moyenne. Ou prenez la médiane du gradient au lieu de la moyenne pour réduire l'impact des valeurs aberrantes du gradient.

Résumé

Quelques mots à la fin de l'article Si vous êtes intéressé par la théorie de l'apprentissage profond, vous pouvez lire les recherches connexes mentionnées dans l'article.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!