
Cet article porte sur le travail d'apprentissage par renforcement profond pour résister aux attaques. Dans cet article, l'auteur étudie la robustesse des stratégies d'apprentissage par renforcement profond face aux attaques adverses dans la perspective d'une optimisation robuste. Dans le cadre d'une optimisation robuste, des attaques adverses optimales sont obtenues en minimisant le retour attendu de la stratégie et, par conséquent, un bon mécanisme de défense est obtenu en améliorant les performances de la stratégie face au pire des cas.
Considérant que les attaquants ne peuvent généralement pas attaquer dans l'environnement d'entraînement, l'auteur propose un algorithme d'attaque glouton qui tente de minimiser le retour attendu de la stratégie sans interagir avec l'environnement. De plus, l'auteur propose également un algorithme de défense, cet algorithme utilise ; un jeu max-min pour mener une formation contradictoire d'algorithmes d'apprentissage par renforcement profond.
Les résultats expérimentaux dans l'environnement de jeu Atari montrent que l'algorithme d'attaque contradictoire proposé par l'auteur est plus efficace que l'algorithme d'attaque existant et que le taux de retour de la stratégie est pire. Les stratégies générées par l’algorithme de défense contradictoire proposé dans le document sont plus robustes à une gamme d’attaques contradictoires que les méthodes de défense existantes.
Étant donné n'importe quel échantillon (x, y) et réseau neuronal f, l'objectif d'optimisation de la génération d'un échantillon contradictoire est :
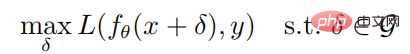
où est le paramètre du réseau neuronal f, L is La fonction de perte est un ensemble de perturbations contradictoires, et  est une boule contrainte par une norme avec x comme centre et radius comme rayon. La formule de calcul pour générer des échantillons adverses via des attaques PGD est la suivante :
est une boule contrainte par une norme avec x comme centre et radius comme rayon. La formule de calcul pour générer des échantillons adverses via des attaques PGD est la suivante :
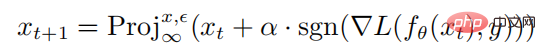
où  représente l'opération de projection Si l'entrée est en dehors de la sphère normale, l'entrée est projetée sur la sphère de centre x et de rayon, ce qui signifie est la taille de la perturbation en une seule étape de l'attaque PGD.
représente l'opération de projection Si l'entrée est en dehors de la sphère normale, l'entrée est projetée sur la sphère de centre x et de rayon, ce qui signifie est la taille de la perturbation en une seule étape de l'attaque PGD.
2.2 Apprentissage par renforcement et gradients politiques
Un problème d'apprentissage par renforcement peut être décrit comme un processus de décision markovien. Le processus de décision de Markov peut être défini comme un 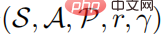 quintuple, où S représente un espace d'état, A représente un espace d'action,
quintuple, où S représente un espace d'état, A représente un espace d'action, 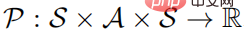 représente la probabilité de transition d'état, r représente la fonction de récompense et représente le facteur d'actualisation. Le but de l'apprentissage fort est d'apprendre une distribution de politique de paramètres
représente la probabilité de transition d'état, r représente la fonction de récompense et représente le facteur d'actualisation. Le but de l'apprentissage fort est d'apprendre une distribution de politique de paramètres  pour maximiser la fonction de valeur
pour maximiser la fonction de valeur
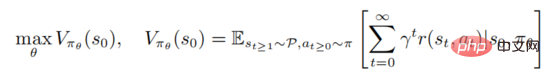
où représente l'état initial. Un apprentissage solide implique l'évaluation de la fonction de valeur d'action
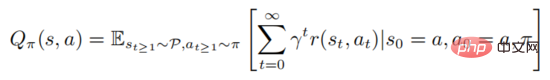
La formule ci-dessus décrit l'attente mathématique d'obéir à la politique après l'exécution de l'État. On peut savoir d'après la définition que la fonction valeur et la fonction valeur d'action satisfont la relation suivante :
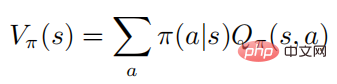
Pour faciliter l'expression, l'auteur se concentre principalement sur le processus de Markov de l'espace d'action discret, mais tous les algorithmes et résultats peut être directement appliqué aux réglages continus Certainement.
La stratégie d'attaque et de défense contradictoire de l'apprentissage par renforcement profond est basée sur le cadre d'optimisation robuste PGD
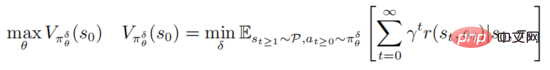
où représente  , représente l'ensemble des séquences de perturbations contradictoires
, représente l'ensemble des séquences de perturbations contradictoires  , et pour toutes
, et pour toutes 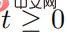 , satisfait
, satisfait 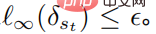 La formule ci-dessus fournit un cadre unifié pour un apprentissage par renforcement profond pour combattre les attaques et les défenses.
La formule ci-dessus fournit un cadre unifié pour un apprentissage par renforcement profond pour combattre les attaques et les défenses.
D'une part, l'optimisation de minimisation interne recherche les séquences de perturbations contradictoires qui amènent la stratégie actuelle à prendre de mauvaises décisions. D'autre part, le but de la maximisation externe est de trouver les paramètres de distribution de la stratégie permettant de maximiser le rendement attendu dans le cadre de la stratégie de perturbation. Après les attaques contradictoires et les jeux de défense ci-dessus, les paramètres stratégiques pendant le processus de formation seront plus résistants aux attaques contradictoires.
Le but de la minimisation interne de la fonction objectif est de générer des perturbations contradictoires. Cependant, pour les algorithmes d'apprentissage par renforcement, l'apprentissage des perturbations contradictoires optimales prend beaucoup de temps et de main-d'œuvre, et comme l'environnement de formation est une boîte noire pour l'utilisateur. attaquant, Ainsi, dans cet article, l'auteur considère un cadre pratique, dans lequel l'attaquant injecte des perturbations dans différents états. Dans le scénario d'attaque par apprentissage supervisé, l'attaquant n'a qu'à tromper le modèle de classificateur pour le faire mal classer et produire des étiquettes erronées ; dans le scénario d'attaque par apprentissage par renforcement, la fonction de valeur d'action fournit à l'attaquant des informations supplémentaires, c'est-à-dire une petite valeur de comportement ; entraînera un petit retour attendu. De manière correspondante, l'auteur définit la perturbation contradictoire optimale dans l'apprentissage par renforcement profond comme suit
Définition 1 : Une perturbation contradictoire optimale sur les états peut minimiser le retour attendu de l'état
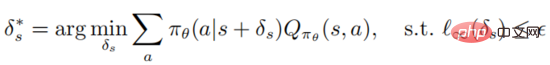
Il convient de noter que l'optimisation résout la formule ci-dessus est très délicat. Il faut garantir que l'attaquant peut tromper l'agent en lui faisant choisir le pire comportement de prise de décision. Cependant, la fonction de valeur d'action de l'agent est inconnue de l'attaquant, il n'y a donc aucune garantie que la perturbation adverse soit optimale. . Le théorème suivant peut montrer que si la politique est optimale, la perturbation adverse optimale peut être générée sans accéder à la fonction de valeur d'action
Théorème 1 : Lorsque la stratégie de contrôle 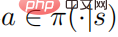 est optimale, la fonction de valeur d'action et la politique satisfont la relation suivante
est optimale, la fonction de valeur d'action et la politique satisfont la relation suivante
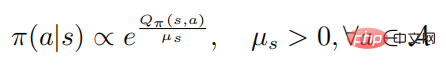
où représente l'entropie de la politique, est une constante dépendante de l'état, et lorsqu'elle passe à 0, elle passera également à 0, puis la formule suivante
prouve : Lorsque la stratégie aléatoire 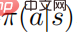 atteint l'optimal Quand , le la fonction valeur
atteint l'optimal Quand , le la fonction valeur 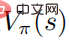 atteint également l'optimum, ce qui signifie que dans chaque état s, aucune autre distribution de comportement ne peut être trouvée pour faire augmenter la fonction valeur
atteint également l'optimum, ce qui signifie que dans chaque état s, aucune autre distribution de comportement ne peut être trouvée pour faire augmenter la fonction valeur 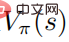 . De manière correspondante, étant donné la fonction de valeur d'action optimale
. De manière correspondante, étant donné la fonction de valeur d'action optimale 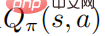 , la stratégie optimale
, la stratégie optimale 
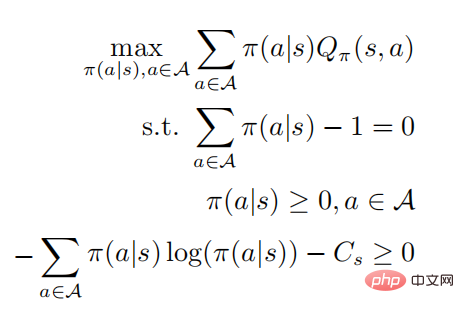
peut être obtenue en résolvant le problème d'optimisation contrainte. Les deuxième et troisième lignes indiquent qu'il s'agit d'une distribution de probabilité, et la dernière ligne indique que la stratégie est. une stratégie aléatoire. , selon les conditions KKT, le problème d'optimisation ci-dessus peut être transformé sous la forme suivante :
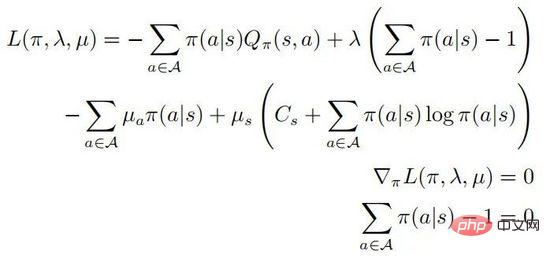
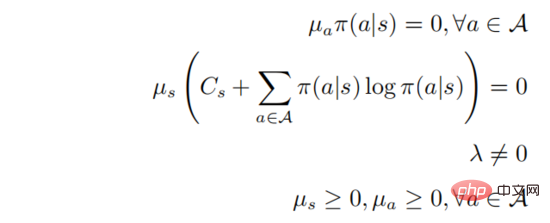
Parmi eux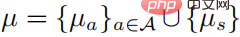 . Supposons que
. Supposons que 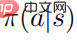 est défini positif pour tous les comportements
est défini positif pour tous les comportements 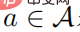 , alors nous avons :
, alors nous avons :
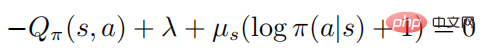
Quand 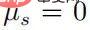 , alors il doit y avoir
, alors il doit y avoir 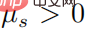 , et puis pour tout
, et puis pour tout 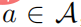 , alors il y a
, alors il y a 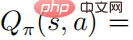 , nous pouvons donc obtenir la relation entre la valeur de l'action fonction et le softmax de la stratégie
, nous pouvons donc obtenir la relation entre la valeur de l'action fonction et le softmax de la stratégie
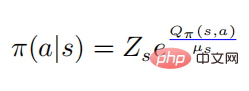
parmi eux  , et ensuite nous avons
, et ensuite nous avons
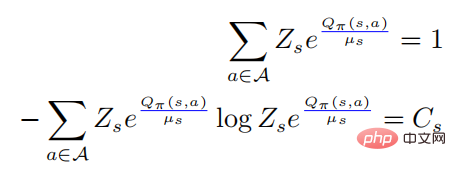
En introduisant la première équation ci-dessus dans la seconde, nous avons
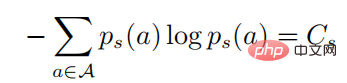
parmi lesquelles
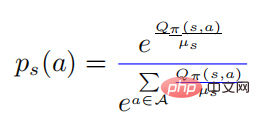
. dans la formule ci-dessus signifie 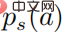 Une distribution de probabilité sous la forme d'un softmax avec une entropie égale à . Quand est égal à 0, devient également 0. Dans ce cas, est supérieur à 0, alors
Une distribution de probabilité sous la forme d'un softmax avec une entropie égale à . Quand est égal à 0, devient également 0. Dans ce cas, est supérieur à 0, alors  à ce moment.
à ce moment.
Le Théorème 1 montre que si la politique est optimale, la perturbation optimale peut être obtenue en maximisant l'entropie croisée de la politique perturbée et de la politique d'origine. Pour simplifier la discussion, l'auteur appelle l'attaque du théorème 1 une attaque stratégique, et l'auteur utilise le cadre d'algorithme PGD pour calculer l'attaque stratégique optimale. L'organigramme spécifique de l'algorithme est présenté dans l'algorithme 1 ci-dessous.

L'organigramme de l'algorithme d'optimisation robuste pour la défense contre les perturbations proposé par l'auteur est présenté dans l'algorithme 2 ci-dessous. Cet algorithme est appelé entraînement contradictoire aux attaques stratégiques. Pendant la phase de formation, la politique de perturbation est utilisée pour interagir avec l'environnement, et en même temps, la fonction de valeur d'action 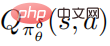 de la politique de perturbation est estimée pour faciliter la formation des politiques.
de la politique de perturbation est estimée pour faciliter la formation des politiques.
Les détails spécifiques sont que d'abord, l'auteur utilise des attaques stratégiques pour générer des perturbations pendant la phase d'entraînement, même s'il n'est pas garanti que la fonction de valeur soit réduite. Au début de la formation, la politique peut ne pas être liée à la fonction de valeur d'action. Au fur et à mesure que la formation progresse, elle satisfera progressivement la relation softmax.
D'un autre côté, les auteurs doivent estimer avec précision la fonction de valeur d'action 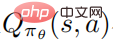 , ce qui est difficile à gérer car les trajectoires sont collectées en exécutant la politique perturbée, et utiliser ces données pour estimer la fonction de valeur d'action de la politique non perturbée peut être très inexacte.
, ce qui est difficile à gérer car les trajectoires sont collectées en exécutant la politique perturbée, et utiliser ces données pour estimer la fonction de valeur d'action de la politique non perturbée peut être très inexacte.

La fonction objectif de la stratégie de perturbation optimisée 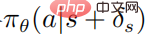 utilisant PPO est
utilisant PPO est
où 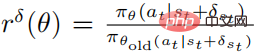 , et
, et  est une estimation de la fonction moyenne
est une estimation de la fonction moyenne  de la stratégie de perturbation. En pratique,
de la stratégie de perturbation. En pratique,  est estimé par la méthode GAE. L'organigramme de l'algorithme spécifique est présenté dans la figure ci-dessous.
est estimé par la méthode GAE. L'organigramme de l'algorithme spécifique est présenté dans la figure ci-dessous.

Les trois sous-figures à droite ci-dessous montrent les résultats de différentes perturbations d'attaque. On peut constater que la politique inversement entraînée et la politique standard résistent aux perturbations aléatoires. En revanche, les attaques contradictoires dégradent les performances des différentes stratégies. Les résultats dépendent de l’environnement de test et de l’algorithme de défense, et on peut en outre constater que l’écart de performances entre les trois algorithmes d’attaque contradictoire est faible.
En revanche, dans des contextes relativement difficiles, la stratégie proposée par les auteurs de l'article pour s'attaquer aux interférences des algorithmes produit des rendements bien inférieurs. Dans l’ensemble, l’algorithme d’attaque stratégique proposé dans l’article produit la récompense la plus faible dans la plupart des cas, ce qui indique qu’il s’agit effectivement du plus efficace de tous les algorithmes d’attaque contradictoire testés.

Comme le montre la figure ci-dessous, les courbes d'apprentissage des différents algorithmes de défense et du PPO standard sont présentées. Il est important de noter que la courbe de performance ne représente que le rendement attendu de la stratégie utilisée pour interagir avec l'environnement. Parmi tous les algorithmes de formation, l'ATPA proposé dans l'article présente la variance de formation la plus faible et est donc plus stable que les autres algorithmes. Notez également que l'ATPA progresse beaucoup plus lentement que le PPO standard, en particulier dans les premiers stades de formation. Cela conduit au fait qu'au début de la formation, le fait d'être perturbé par des facteurs défavorables peut rendre la formation politique très instable.
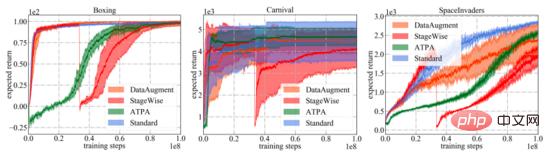
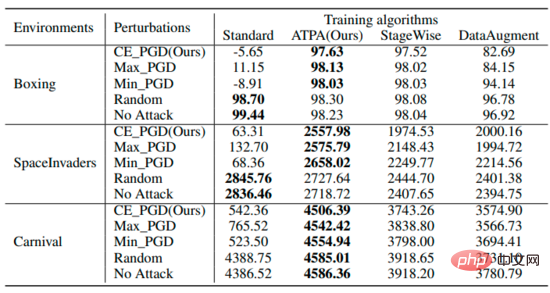
Le tableau résume les rendements attendus des stratégies utilisant différents algorithmes sous différentes perturbations. On peut constater que les stratégies formées par l’ATPA résistent à diverses interférences adverses. En comparaison, bien que StageWise et DataAugment aient appris à gérer les attaques contradictoires dans une certaine mesure, ils ne sont pas aussi efficaces que l’ATPA dans tous les cas.
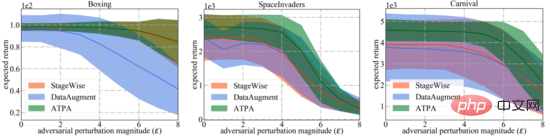
Pour une comparaison plus large, les auteurs évaluent également la robustesse de ces algorithmes de défense face à différents degrés d'interférence adverse générés par les algorithmes d'attaque stratégique les plus efficaces. Comme indiqué ci-dessous, l’ATPA a une fois de plus obtenu les scores les plus élevés dans tous les cas. De plus, la variance d'évaluation de l'ATPA est beaucoup plus petite que celle de StageWise et DataAugment, ce qui indique que l'ATPA a une capacité générative plus forte.
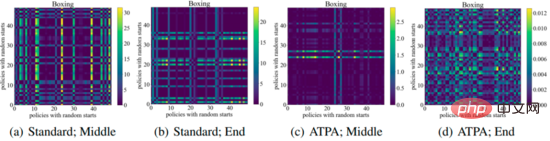
Pour obtenir des performances similaires, l'ATPA nécessite plus de données d'entraînement que l'algorithme PPO standard. Les auteurs approfondissent cette question en étudiant la stabilité de la stratégie de perturbation. Les auteurs ont calculé les valeurs de divergence KL de la politique de perturbation obtenues en effectuant des attaques de politique à l'aide de PGD avec différents points initiaux aléatoires au milieu et à la fin du processus de formation. Comme le montre la figure ci-dessous, sans formation contradictoire, de grandes valeurs de divergence KL sont constamment observées même lorsque le PPO standard a convergé, ce qui indique que la politique est très instable aux perturbations produites par la réalisation du DPI avec différents points initiaux.
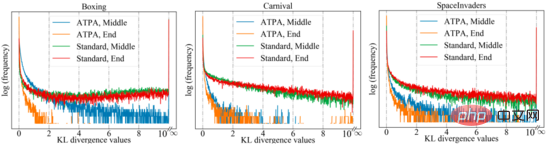
La figure suivante montre le tracé de divergence KL des stratégies de perturbation avec différents points initiaux. On peut constater que chaque pixel de la figure représente la valeur de divergence KL de deux stratégies de perturbation maximisent l'ATPA La formule de base. de l’algorithme est donné. Notez que puisque la divergence KL est une métrique asymétrique, ces mappages sont également asymétriques.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Page d'erreur 404 de l'ordinateur
Page d'erreur 404 de l'ordinateur
 Solution à l'invite de table de partition non valide au démarrage de Windows 10
Solution à l'invite de table de partition non valide au démarrage de Windows 10
 Comment résoudre le problème de ssleay32.dll manquant
Comment résoudre le problème de ssleay32.dll manquant
 Comment définir l'IP
Comment définir l'IP
 Comment ouvrir le fichier d'état
Comment ouvrir le fichier d'état
 Pourquoi le disque dur mobile est-il si lent à s'ouvrir ?
Pourquoi le disque dur mobile est-il si lent à s'ouvrir ?
 Quelles sont les unités de base du langage C ?
Quelles sont les unités de base du langage C ?
 Quelle plateforme est Kuai Tuan Tuan ?
Quelle plateforme est Kuai Tuan Tuan ?