
Cet article vous apporte des connaissances pertinentes sur java L'algorithme Prime est un algorithme de recherche exhaustif pour construire un arbre couvrant minimum à partir d'un graphe connecté. Cet article présente principalement le principe et l'implémentation de l'algorithme Prime en Java. Si vous êtes intéressé, vous pouvez en apprendre davantage.

Apprentissage recommandé : "Tutoriel vidéo Java"
Dans le processus de spanning tree, traitez les nœuds déjà dans le spanning tree comme un ensemble, et mettre le reste Les nœuds sont considérés comme un autre ensemble et l'arête avec le plus petit poids peut être sélectionnée parmi les arêtes reliant les deux ensembles.
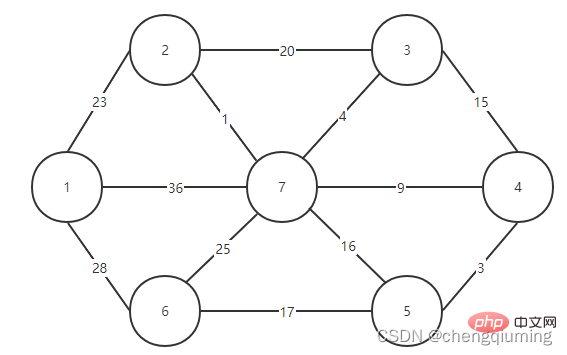
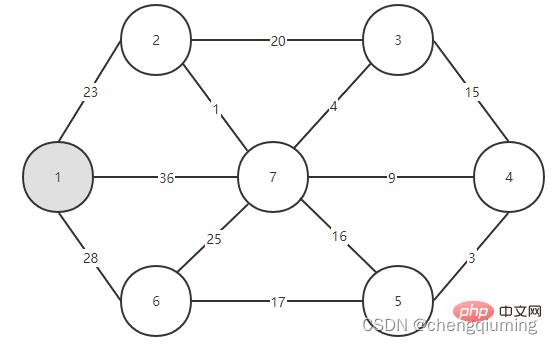
Sélectionnez d'abord un nœud, tel que le nœud 1, et placez-le dans l'ensemble U, U={1}, puis les nœuds restants sont V-U={2,3,4, 5. ,6,7}, l'ensemble V est l'ensemble de tous les nœuds du graphe.
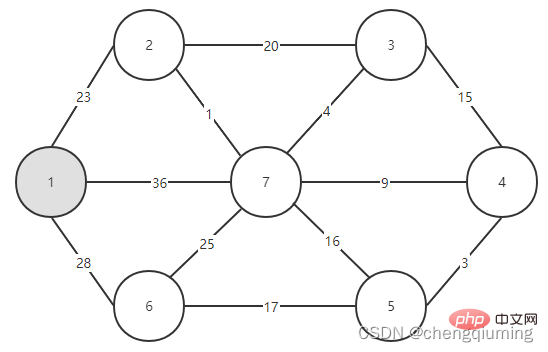
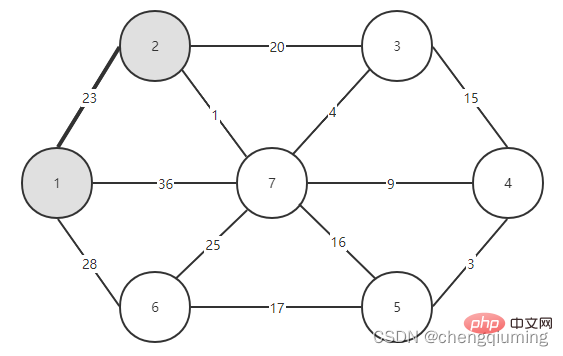
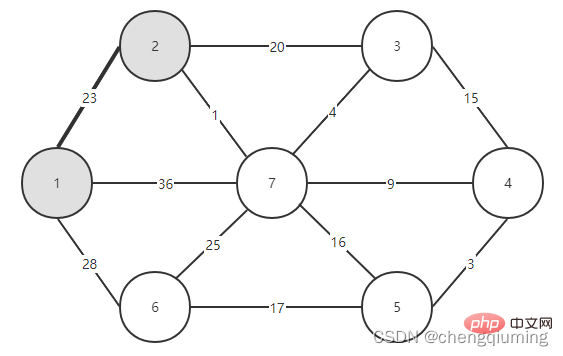
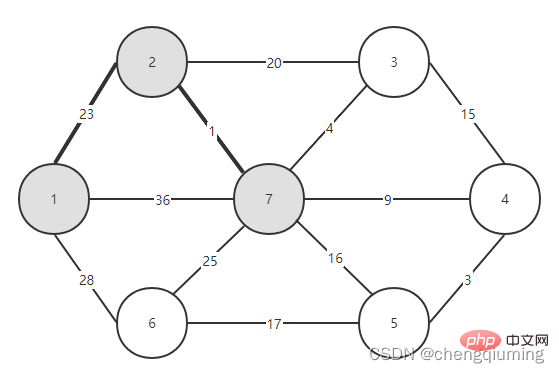
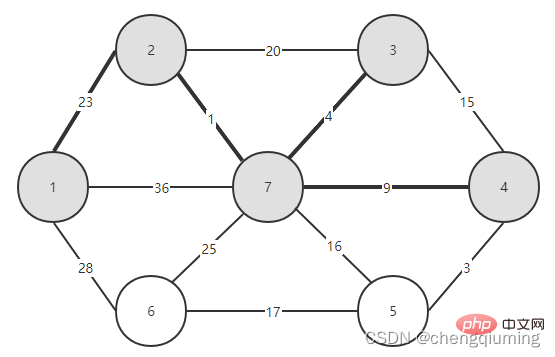
Il ne vous reste plus qu'à voir quelle arête a le plus petit poids parmi les arêtes reliant les deux ensembles (U et V-U), et ajouter le nœud associé à l'arête avec le plus petit poids à l'ensemble U. Comme le montre la figure ci-dessus, parmi les 3 arêtes reliant les deux ensembles, l'arête 1-2 a le plus petit poids. Sélectionnez-le et ajoutez le nœud 2 à l'ensemble U, U={1,2}, V - U=. { 3,4,5,6}, comme le montre la figure ci-dessous.
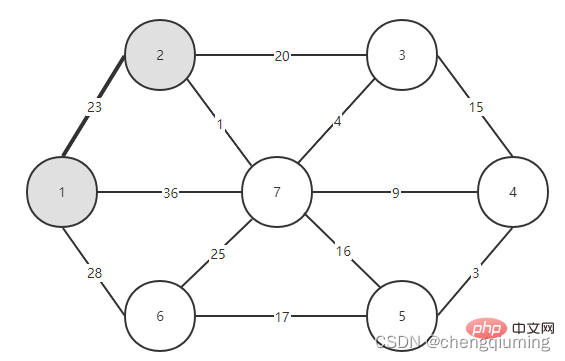
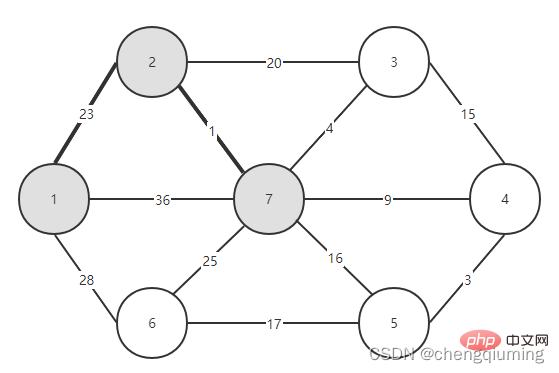
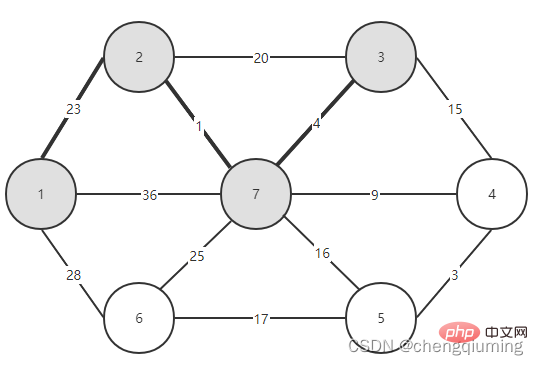
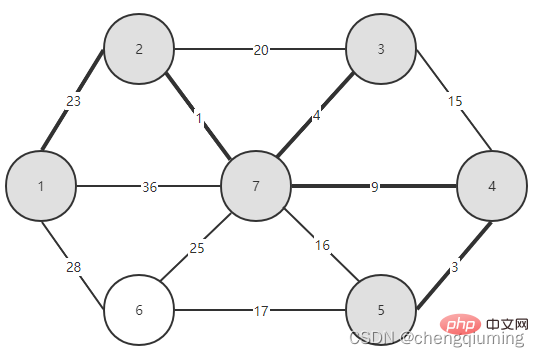
Sélectionnez ensuite la bordure ayant le plus petit poids parmi les bordures reliant les deux ensembles (U et V-U). Comme le montre la figure ci-dessus, parmi les quatre arêtes reliant les deux ensembles, le poids de l'arête du nœud 2 au nœud 7 est le plus petit. Sélectionnez cette arête et ajoutez le nœud 7 à l'ensemble U={1,2,7}. , V-U ={3,4,5,6}.
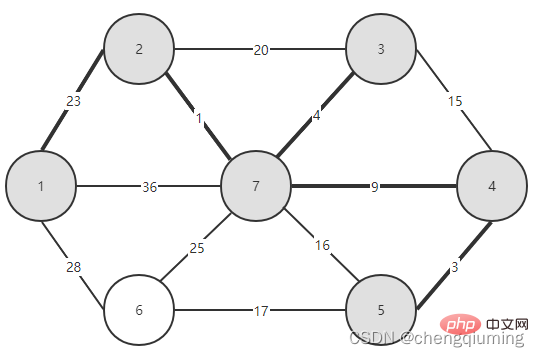
Continuez ainsi jusqu'à ce que U=V se termine et que le graphique composé de l'arête sélectionnée et de tous les nœuds soit l'arbre couvrant minimum. C'est l'algorithme de Prim.
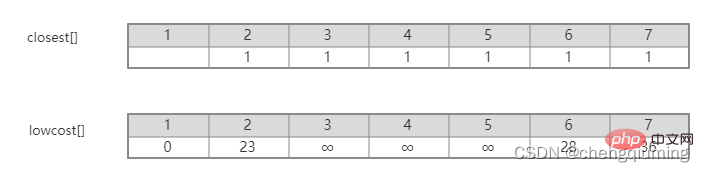
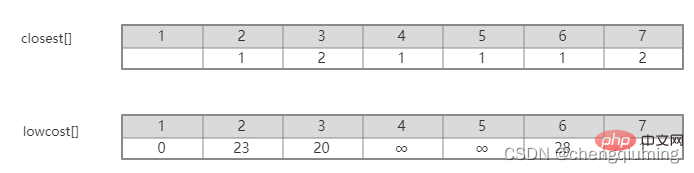
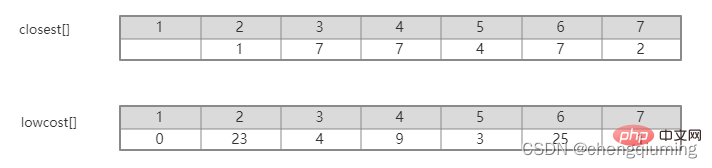
En regardant intuitivement l'image, il est facile de savoir quelle arête de l'ensemble U à l'ensemble U-V a le plus petit poids. Cependant, la complexité temporelle est trop élevée pour énumérer de manière exhaustive ces arêtes dans le programme et ensuite trouver le minimum. valeur. Ce problème peut être résolu intelligemment en définissant un tableau Closet[j] qui représente le point voisin le plus proche du nœud j dans l'ensemble V-U à l'ensemble U. Lowcost[j] représente la valeur de bord du nœud j dans l'ensemble V-U au point voisin le plus proche dans. définir U. C'est-à-dire le poids du bord (j, le plus proche[j]).
Par exemple, dans la figure ci-dessus, le point voisin le plus proche du nœud 7 à l'ensemble U est 2, cloeest[7]=2. La valeur du bord du nœud 7 au point voisin le plus proche 2 est 1, qui est le poids du bord (2,7), enregistré comme lowcost[7]=1, comme le montre la figure ci-dessous.
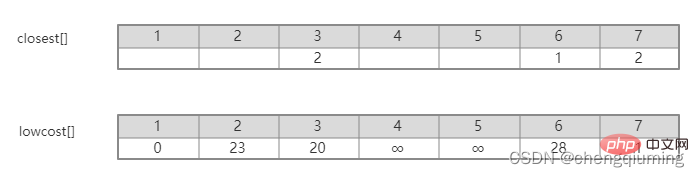
Il suffit donc de trouver le nœud lowcost[] le plus bas dans l'ensemble V - U.
1. Initialiser
Laissez l'ensemble U={u0}, u0 appartenir à V, et initialisez les tableaux les plus proches[], lowcost[] et s[].
2. Trouvez le nœud t avec la plus petite valeur lowcost dans l'ensemble V-U, c'est-à-dire lowcost[t]=min{lowcost[j]}, j appartient à V-U. Le nœud t qui satisfait cette formule est le point le plus proche. reliant U dans l'ensemble V-U .
3. Ajoutez le nœud t à l'ensemble U.
4. Si l'ensemble V - U est vide, l'algorithme se termine, sinon passez à l'étape 5.
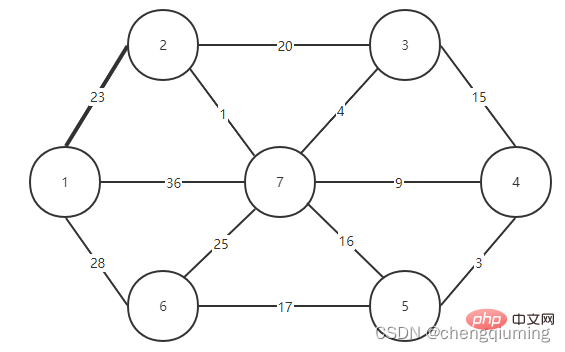
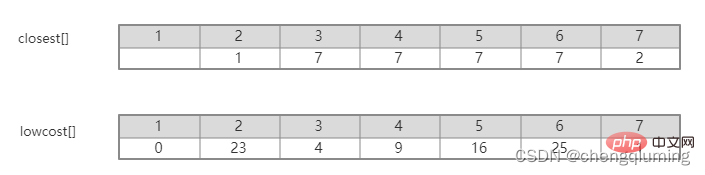
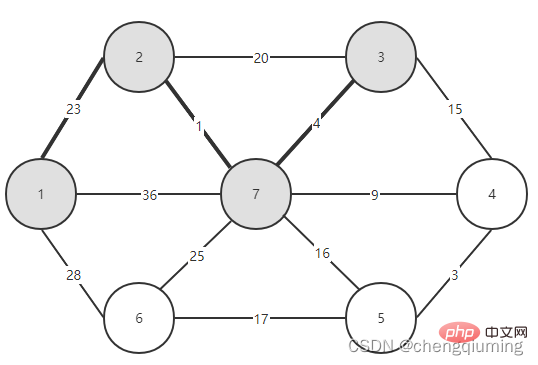
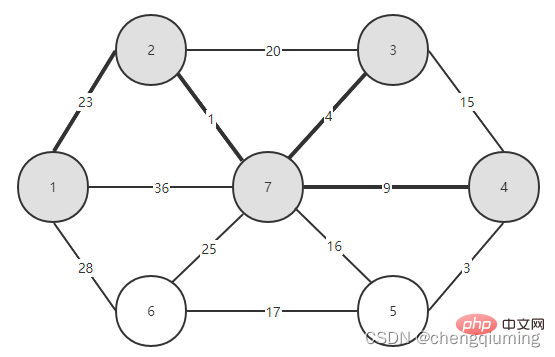
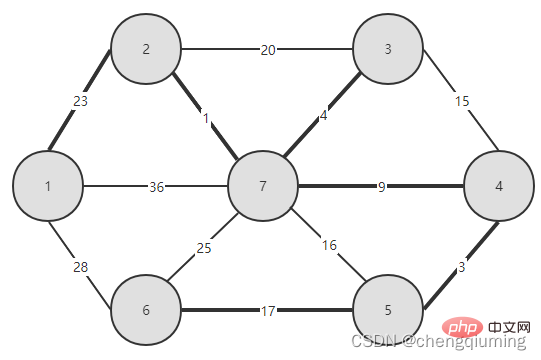
5. Mettez à jour son lowcost[] et le plus proche[] pour tous les nœuds j de l'ensemble V-U. if(C[t][j] Suivez les étapes ci-dessus et vous pourrez enfin obtenir un arbre couvrant avec la plus petite somme de poids. Le graphe G=(V,E) est un graphe pondéré connecté non orienté, comme le montre la figure ci-dessous. 1 Initialisation. Supposons que u0=1, soit l'ensemble U={1}, l'ensemble V-U={2,3,4,5,6,7}, s[1]=true, initialise le tableau le plus proche[] : sauf le nœud 1, tous les autres nœuds sont égaux à 1, ce qui signifie que les points voisins les plus proches des nœuds de l'ensemble V-U à l'ensemble U sont tous 1.lowcost[] : la valeur du bord du nœud 1 au nœud de l'ensemble V-U. close[] et lowcost[] sont illustrés dans la figure ci-dessous. L'image après initialisation est : 2 Trouvez le nœud avec le plus petit faible coût, correspondant à t=2. Les arêtes et nœuds sélectionnés sont comme indiqué ci-dessous. 3 est ajouté à l'ensemble U. Ajoutez le nœud t à l'ensemble U, U={1,2} et mettez à jour V-U={3,4,5,6,7} 4 en même temps. Pour chaque point adjacent j de t dans l'ensemble V-U, il peut être mis à jour à l'aide de t. Les points adjacents du nœud 2 sont le nœud 3 et le nœud 7. C[2][3]=20 C[2][7]= 1< lowcost[7]=36, mettez à jour la distance du voisin le plus proche lowcost[7]=1, le voisin le plus proche le plus proche[7]=2; Les valeurs les plus proches[] et lowcost[] mises à jour sont comme indiqué dans la figure ci-dessous. L'ensemble mis à jour est le suivant : 5 Trouvez le nœud avec le plus petit faible coût, correspondant à t=7, et les arêtes et nœuds sélectionnés sont comme indiqué ci-dessous. 6 Ajouter au set U. Ajoutez le nœud t à l'ensemble U, U={1,2,7} et mettez à jour V-U={3,4,5,6} 7 en même temps. Pour chaque point adjacent j de t dans l'ensemble V-U, il peut être mis à jour à l'aide de t. Les points adjacents du nœud 7 sont les nœuds 3, 4, 5 et 6. Les points les plus proches[] et lowcost[] mis à jour sont indiqués dans la figure ci-dessous. L'ensemble mis à jour est le suivant : 8 Trouvez le nœud avec le plus petit faible coût, correspondant à t=3, et les arêtes et nœuds sélectionnés sont comme indiqué ci-dessous. 9 est ajouté à l'ensemble U. Ajoutez le nœud t à l'ensemble U, U={1,2,3,7} et mettez à jour V-U={4,5,6} 10 en même temps. Pour chaque point adjacent j de t dans l'ensemble V-U, il peut être mis à jour à l'aide de t. Le voisin du nœud 3 est le nœud 4. C[3][4]=15>lowcost[4]=9, les tableaux closest[] et lowcost[] ne changent pas. L'ensemble mis à jour est le suivant : 11 Trouvez le nœud avec le plus petit faible coût, correspondant à t=4, et les arêtes et nœuds sélectionnés sont comme indiqué ci-dessous. 12 ajoutés à l'ensemble U. Ajoutez le nœud t à l'ensemble U, U={1,2,3,4,7} et mettez à jour V-U={5,6} 13 en même temps. Pour chaque point adjacent j de t dans l'ensemble V-U, il peut être mis à jour à l'aide de t. Le voisin du nœud 4 est le nœud 5. C[4][5]=3 mis à jour le plus proche[] et lowcost [] Comme montré ci-dessous. L'ensemble mis à jour est le suivant : 14 Trouvez le nœud avec le plus petit faible coût, correspondant à t=5, et les arêtes et nœuds sélectionnés sont comme indiqué ci-dessous. 15 ajoutés à l'ensemble U. Ajoutez le nœud t à l'ensemble U, U={1,2,3,4,5,7} et mettez à jour V-U={6} 16 en même temps. Pour chaque point adjacent j de t dans l'ensemble V-U, il peut être mis à jour à l'aide de t. Le voisin du nœud 5 est le nœud 6. C[5][6]=17 L'ensemble mis à jour est le suivant : 17 Trouvez le nœud avec le plus petit faible coût, correspondant à t=6. Les arêtes et nœuds sélectionnés sont comme indiqué ci-dessous. 18 ajoutés à l'ensemble U. Ajoutez le nœud t à l'ensemble U, U={1,2,3,4,5,6,7} et mettez à jour V-U={} 19 en même temps. Pour chaque point adjacent j de t dans l'ensemble V-U, il peut être mis à jour à l'aide de t. Le nœud 6 n'a pas de points adjacents dans l'ensemble V-U. Pas besoin de mettre à jour close[] et lowcost[]. 20 L'arbre couvrant minimum obtenu est le suivant. La somme des poids de l'arbre couvrant minimum est de 57. Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!4. Diagramme
Implémentation de l'algorithme Prime
1 Le graphique construit
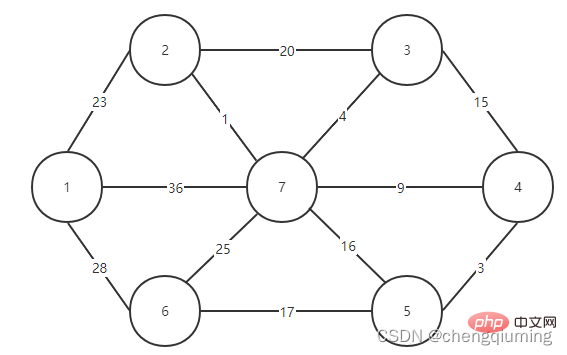
2. Tutoriel vidéo Java
"