
Le contenu de cet article concerne l'implémentation de la méthode Monte Carlo (exemple de code) en Python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.
La méthode de Monte Carlo est une méthode de simulation statistique proposée par von Neumann et Ulam. Sous un grand nombre de nombres aléatoires, selon les résultats de l'estimation de probabilité, plus il y a de données aléatoires, plus les résultats sont. plus précis. Ci-dessous, nous utiliserons python pour implémenter la méthode Monte Carlo.
1. Tout d'abord, nous effectuons un simple calcul approximatif de pi Dans ce processus, nous devons utiliser des nombres aléatoires, nous devons donc d'abord utiliser import numpy as np pour importer la bibliothèque numpy.
2. Implémentation du code :
import numpy as np
total = 8000000
count = 0
for i in range(total):
x = np.random.rand()
y = np.random.rand()
dis = (x**2+y**2)**0.5
if dis <p>3. Dans le programme ci-dessus, nous utilisons 8 000 000 nombres aléatoires pour la livraison, afin que le résultat soit plus précis. L'exécution du programme nécessite un certain nombre. laps de temps, le résultat final est le suivant </p><p><span class="img-wrap"><img src="https://img.php.cn//upload/image/549/675/172/1547436392667253.png" title="1547436392667253.png" alt="Python implémente la méthode Monte Carlo (exemple de code)"></span></p><p>4 Faisons une application simple. L'image ci-dessous est ce que j'ai dessiné avec désinvolture dans le. outil de dessin. Pour un graphique, nous pouvons utiliser la méthode de Monte Carlo pour estimer l'aire de la partie noire du graphique. </p><p style="max-width:90%"><span class="img-wrap"><img src="https://img.php.cn//upload/image/583/174/740/1547436406520588.png" title="1547436406520588.png" alt="Python implémente la méthode Monte Carlo (exemple de code)"></span></p><p>5. Le graphique ci-dessus est irrégulier, il suffit de savoir que lorsqu'un grand nombre de nombres aléatoires sont lancés, les nombres aléatoires apparaissent dans la probabilité de la partie noire, puis multipliez la superficie totale pour estimer la superficie de la partie noire. Nous savons que le code RVB noir est (0,0,0), nous devons donc calculer la probabilité de nombres aléatoires lorsque le code RVB est (0,0,0). </p><p>6. Implémentation du code : </p><pre class="brush:php;toolbar:false">from PIL import Image
import numpy as np
im = Image.open("C:/Users/21974/Desktop/handwrite2.PNG")
total = 9000000
count = 0
defin = 0
width = im.size[0]
height = im.size[1]
for i in range(total): #用蒙特卡罗方法获得估计值
x = np.random.randint(0, width-1)
y = np.random.randint(0, height-1)
k = im.getpixel((x, y))
if k[0]+k[1]+k[2] == 0:
count += 1
print(int(width*height*count/total))
for i in range(width): #用遍历获得准确值
for j in range(height):
k = im.getpixel((i, j))
if k[0] + k[1] + k[2] == 0:
defin += 1
print(defin)Le code ci-dessus peut être divisé en deux parties. La première est suivie de la valeur estimée de la surface obtenue par la méthode de Monte Carlo, et le second Le for est suivi de la valeur exacte de la zone obtenue en parcourant tous les pixels, et la comparaison est effectuée après l'obtention des deux sorties.
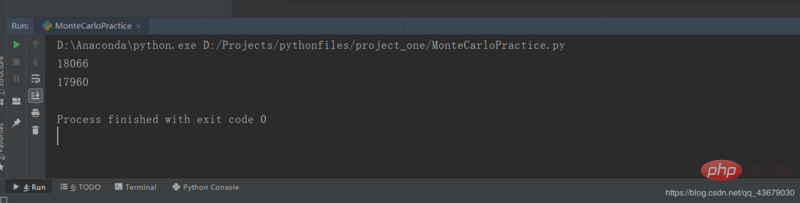
Nous avons utilisé 9 000 000 nombres aléatoires dans le programme ci-dessus. On peut voir que les deux résultats de sortie ne sont pas très différents.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!