
Cet article vous présente principalement les informations pertinentes sur l'utilisation du CSS pour réaliser des exemples de flèches de n'importe quelle taille, n'importe quelle direction et n'importe quel angle. L'éditeur pense que c'est plutôt bien. Maintenant, je vais le partager avec vous et vous donner une référence. J'espère que cela pourra être utile à tout le monde.
Dans le développement Web, la flèche déroulante

est souvent utilisée, et la flèche droite

Une telle flèche. Il est généralement implémenté en utilisant CSS :
{
display: inline-block;
margin: 72px;
border-top: 24px solid;
border-right: 24px solid;
width: 120px;
height: 120px;
transform: rotate(45deg);
}car cela est réalisé en utilisant la bordure supérieure et la bordure droite de p, puis en faisant pivoter le p.
Flèches à n'importe quel angle
Voici une question : Et si vous avez besoin d'une flèche avec un angle de 120 degrés ? Étant donné que les bordures supérieure et droite sont toujours à 90 degrés, une simple rotation ne fonctionnera pas. Nous pouvons d’abord faire pivoter p de 45 degrés pour en faire un losange, puis l’étirer pour atteindre n’importe quel angle, afin d’obtenir une flèche sous n’importe quel angle. Puisque deux transformations, rotation et mise à l'échelle, sont utilisées, la matrice de transformation transform: matrix(a,b,c,d,e,f) doit être utilisée. Les 6 variables forment ici une matrice de transformation tridimensionnelle
La translation, la rotation, la transformation d'expansion et diverses combinaisons de tout point p (x, y) peuvent être réalisées grâce à cette matrice de transformation :
Remarque : Des coordonnées homogènes sont utilisées ici pour exprimer un point. En termes simples, p(x, y) est exprimé comme p'(x', y', 1)
Matrice de traduction
v(x, y) traduit tx le long de l'axe des x , le long de Translate ty le long de l'axe y. Ensuite il y a :
x' = x + tx
y' = y + ty
Donc la matrice de traduction :
Matrice de rotation
Le point v(x, y) subit une rotation θ autour de l'origine jusqu'à v'(x', y')
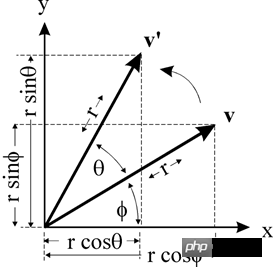
alors il y a :
x = r * cos(ϕ )
y = r * sin(ϕ )x' = r * cos(θ + ϕ) = r * cos(θ ) * cos(ϕ) - r * sin(θ) * sin(ϕ ) // Formule cosinus
y' = r * sin(θ + ϕ) = r * sin(θ) * cos (ϕ) + r * cos(θ) * sin(ϕ ) // Formule sinus
Donc :
x' = x * cos(θ) - y * sin(θ)
y' = x * sin(θ) + y * cos(θ)
Donc la matrice de rotation :
Matrice d'étirement
Supposons que les rapports d'expansion et de contraction de l'axe des x et de l'axe des y sont respectivement kx et ky. Ensuite il y a :
x' = x *kx
y' = y *ky
Donc :
Transformation composite
Et si p(x, y) est d'abord traduit (matrice de transformation A), puis tourné (matrice de transformation B), puis étiré (matrice de transformation C) ?
p ' =C(B(Ap)) ==> p' = (CBA)p //Taux de combinaison de multiplication matricielle
Maintenant, la flèche à n'importe quel angle o est très simple :
Premier p pivote de 45 degrés pour devenir un losange, transformé en M1 Axe x télescopique, axe y :
x' = size * cos(o/2) = x * √2 * cos(o/2) y' = size * sin(o/2) = y * √2 * sin(o/2)
Soit : kx = √2 * cos( o/2); ky = √2 * sin(o/2) De cette façon, une flèche à n'importe quel angle est obtenue. Transformez en M2
Si la direction de la flèche ne pointe pas vers la droite, vous pouvez obtenir une flèche dans n'importe quelle direction en effectuant une rotation. Transformer en M3
Ensuite grâce à p' =C(B(Ap)) ==> p' = (CBA)p, on peut d'abord calculer M3 M2 M1, puis effectuer la transformation correspondante sur p pour obtenir n'importe quel angle, flèches dans n'importe quelle direction.
La largeur et la hauteur de p sont les longueurs des côtés de la flèche. En ajustant, vous pouvez obtenir une flèche avec n'importe quelle longueur de côté.
Composant React
Pour faciliter l'utilisation, cette flèche est encapsulée en tant que composant React.
Exemple
Flèche simple

Simuler la sélection

Flèches divergentes

accessoires
| name | type | default | description |
|---|---|---|---|
| degree | number | 90 | 箭头的张角, 角度制 |
| offsetDegree | number | 0 | 箭头的方向,默认指向右边 |
| color | string | - | 箭头的颜色 |
| size | string | 10px | 箭头边长 |
安装使用
npm install rc-arrow --save
import Arrow from 'rc-arrow'
class Hw extends Component {
render() {
return (
<Arrow size="20px" color="red"/>
)
}
}相关推荐:
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!