Implémentation de l'algorithme de Dijkstra pour l'algorithme du chemin le plus court en Java-javaDidacticiel-php.cn

Cet article présente principalement l'algorithme de chemin le plus court qui implémente l'algorithme de chemin le plus court en Java. L'algorithme de chemin le plus court bien connu est un algorithme de chemin complet à démarrage unique. Ceux qui sont intéressés peuvent en apprendre davantage.

Avant-propos

L'algorithme de Dijkstra est un algorithme de chemin le plus court bien connu et est un algorithme de chemin complet à démarrage unique. Cet algorithme est appelé un exemple réussi d'« algorithme glouton ». Cet article tentera de présenter cet excellent algorithme dans le langage le plus populaire et de lui donner le code d'implémentation Java.

1. Préparation des connaissances :

1. La structure de données représentant le graphique

est. utilisé Il existe de nombreuses structures de données pour stocker des graphiques. Dans cet algorithme, l'auteur utilise la matrice de contiguïté.

La méthode de stockage matriciel de contiguïté d'un graphique consiste à utiliser deux tableaux pour représenter le graphique. Un tableau unidimensionnel stocke les informations sur les sommets dans le graphique, et un tableau bidimensionnel (matrice de contiguïté) stocke les informations sur les arêtes ou les arcs dans le graphique.

Supposons que le graphe G ait n sommets, alors la matrice de contiguïté est une matrice carrée n*n, définie comme :

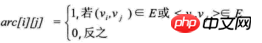
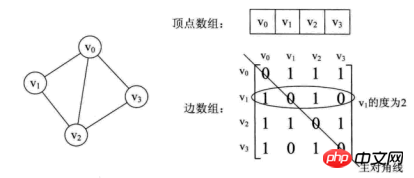
Comme le montre ce qui précède, le tableau de bords d'un graphe non orienté est une matrice symétrique. La matrice dite symétrique signifie que les éléments de la matrice d’ordre n satisfont aij = aji. C'est-à-dire que la diagonale principale du coin supérieur gauche au coin inférieur droit de la matrice est l'axe, et les éléments dans le coin supérieur droit et les éléments correspondants dans le coin inférieur gauche sont tous égaux.

A partir de cette matrice, il est facile de connaître les informations contenues dans l'image.

(1) Il est très facile de déterminer si deux sommets ont des arêtes ou pas d'arêtes

(2) Connaître le degré d'un certain sommet, en fait, cela signifie que le le sommet vi est le troisième dans la matrice de contiguïté La somme des éléments de la ligne i ou (i-ème colonne)

(3) Trouver tous les points adjacents du sommet vi consiste à scanner le i-ème ; éléments de ligne dans la matrice une fois, arc[i][j] vaut 1. Points adjacents

Et les graphiques orientés font attention au degré entrant et sortant du sommet vi est 1, qui est exactement la somme des nombres de la i-ème colonne. Le degré extérieur du sommet vi est 2, qui est la somme des nombres de la ième rangée.

La définition du graphe orienté est également similaire, donc aucun détail ne sera donné.

2. Chemin complet à point de départ unique

Le chemin complet dit à point de départ unique fait référence au chemin le plus court partant d'un point de départ jusqu'à tous les nœuds d'un graphique. .

3. Connaissances de base de la théorie des graphes (les lecteurs doivent trouver les informations pertinentes par eux-mêmes)

Conditions de relaxation complémentaires

Supposons que le scalaire d1, d2,....,dN satisfait

dj<=di + aij, (i,j) appartient à A,

et P est avec i1 comme le point de départ et ik comme chemin du point final, si

dj = di + aij,

est valable pour toutes les arêtes (i, j) de P, alors P est le chemin le plus court depuis i1 à ik. Parmi elles, on appelle les conditions de relaxation complémentaires du problème du plus court chemin qui satisfont aux deux équations ci-dessus.

2. Idée d'algorithme

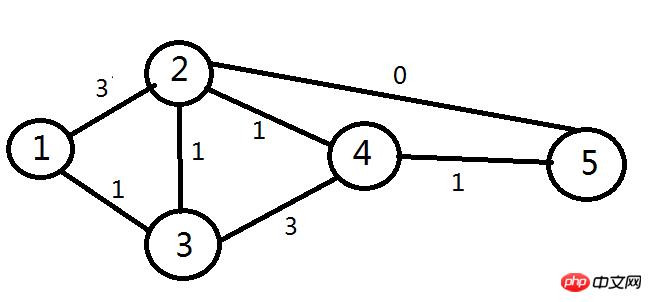
1. Soit G = (V, E) un graphe non orienté pondéré. S'il y a deux nœuds adjacents dans G, i et j. aij (exprimé en indice ici et plus tard, veuillez noter) est le poids du nœud i au nœud j, qui peut être compris comme la distance dans cet algorithme. Chaque nœud a une valeur di (étiquette de nœud) indiquant sa distance entre le point de départ et un certain chemin vers celui-ci.

2. L'algorithme dispose initialement d'un tableau V utilisé pour stocker une liste de nœuds non visités, que nous appelons temporairement la liste candidate. Sélectionnez le nœud 1 comme nœud de départ. Au début, d1=0 pour le nœud 1, di=infini pour les autres nœuds et V représente tous les nœuds.
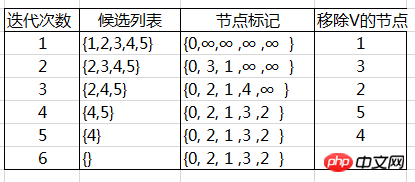
Après avoir initialisé les conditions, démarrez l'algorithme itératif et arrêtez-vous lorsque V est l'ensemble vide. Les étapes d'itération spécifiques sont les suivantes :

Supprimez le nœud di avec la plus petite valeur d de la liste des candidats. (Dans cet exemple, la structure de données de V utilise une file d'attente prioritaire pour implémenter la suppression des valeurs minimales. Il est préférable d'utiliser les paires de Fibonacci, qui ont été présentées dans les articles précédents, et les performances sont grandement améliorées). Pour chaque arête commençant à partir de ce nœud, à l'exclusion du nœud où V est supprimé, (i, j) appartient à A. Si dj > di + aij (violant la condition de relaxation), alors

dj = di + aij , (si j a été retiré de V, cela signifie que sa distance minimale a été calculée et ne participe pas à ce calcul)

On voit que dans le projet de calcul de l'algorithme, le d la valeur du nœud est Le diagramme d'algorithme spécifique de non-augmentation monotone

est le suivant

3. Implémentation du code Java

public class Vertex implements Comparable<Vertex>{

  /**
   * 节点名称(A,B,C,D)
   */
  private String name;
  
  /**
   * 最短路径长度
   */
  private int path;
  
  /**
   * 节点是否已经出列(是否已经处理完毕)
   */
  private boolean isMarked;
  
  public Vertex(String name){
    this.name = name;
    this.path = Integer.MAX_VALUE; //初始设置为无穷大
    this.setMarked(false);
  }
  
  public Vertex(String name, int path){
    this.name = name;
    this.path = path;
    this.setMarked(false);
  }
  
  @Override
  public int compareTo(Vertex o) {
    return o.path > path?-1:1;
  }
}

Copier après la connexion

public class Graph {

  /*
   * 顶点
   */
  private List<Vertex> vertexs;

  /*
   * 边
   */
  private int[][] edges;

  /*
   * 没有访问的顶点
   */
  private Queue<Vertex> unVisited;

  public Graph(List<Vertex> vertexs, int[][] edges) {
    this.vertexs = vertexs;
    this.edges = edges;
    initUnVisited();
  }
  
  /*
   * 搜索各顶点最短路径
   */
  public void search(){
    while(!unVisited.isEmpty()){
      Vertex vertex = unVisited.element();
      //顶点已经计算出最短路径，设置为"已访问"
     　　vertex.setMarked(true);  
      //获取所有"未访问"的邻居
      　　List<Vertex> neighbors = getNeighbors(vertex);  
      //更新邻居的最短路径
      updatesDistance(vertex, neighbors);    
      pop();
    }
    System.out.println("search over");
  }
  
  /*
   * 更新所有邻居的最短路径
   */
  private void updatesDistance(Vertex vertex, List<Vertex> neighbors){
    for(Vertex neighbor: neighbors){
      updateDistance(vertex, neighbor);
    }
  }
  
  /*
   * 更新邻居的最短路径
   */
  private void updateDistance(Vertex vertex, Vertex neighbor){
    int distance = getDistance(vertex, neighbor) + vertex.getPath();
    if(distance < neighbor.getPath()){
      neighbor.setPath(distance);
    }
  }

  /*
   * 初始化未访问顶点集合
   */
  private void initUnVisited() {
    unVisited = new PriorityQueue<Vertex>();
    for (Vertex v : vertexs) {
      unVisited.add(v);
    }
  }

  /*
   * 从未访问顶点集合中删除已找到最短路径的节点
   */
  private void pop() {
    unVisited.poll();
  }

  /*
   * 获取顶点到目标顶点的距离
   */
  private int getDistance(Vertex source, Vertex destination) {
    int sourceIndex = vertexs.indexOf(source);
    int destIndex = vertexs.indexOf(destination);
    return edges[sourceIndex][destIndex];
  }

  /*
   * 获取顶点所有(未访问的)邻居
   */
  private List<Vertex> getNeighbors(Vertex v) {
    List<Vertex> neighbors = new ArrayList<Vertex>();
    int position = vertexs.indexOf(v);
    Vertex neighbor = null;
    int distance;
    for (int i = 0; i < vertexs.size(); i++) {
      if (i == position) {
        //顶点本身，跳过
        continue;
      }
      distance = edges[position][i];  //到所有顶点的距离
      if (distance < Integer.MAX_VALUE) {
        //是邻居(有路径可达)
        neighbor = getVertex(i);
        if (!neighbor.isMarked()) {
          //如果邻居没有访问过，则加入list;
          neighbors.add(neighbor);
        }
      }
    }
    return neighbors;
  }

  /*
   * 根据顶点位置获取顶点
   */
  private Vertex getVertex(int index) {
    return vertexs.get(index);
  }

  /*
   * 打印图
   */
  public void printGraph() {
    int verNums = vertexs.size();
    for (int row = 0; row < verNums; row++) {
      for (int col = 0; col < verNums; col++) {
        if(Integer.MAX_VALUE == edges[row][col]){
          System.out.print("X");
          System.out.print(" ");
          continue;
        }
        System.out.print(edges[row][col]);
        System.out.print(" ");
      }
      System.out.println();
    }
  }
}

Copier après la connexion

public class Test {

  public static void main(String[] args){
    List<Vertex> vertexs = new ArrayList<Vertex>();
    Vertex a = new Vertex("A", 0);
    Vertex b = new Vertex("B");
    Vertex c = new Vertex("C");
    Vertex d = new Vertex("D");
    Vertex e = new Vertex("E");
    Vertex f = new Vertex("F");
    vertexs.add(a);
    vertexs.add(b);
    vertexs.add(c);
    vertexs.add(d);
    vertexs.add(e);
    vertexs.add(f);
    int[][] edges = {
        {Integer.MAX_VALUE,6,3,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {6,Integer.MAX_VALUE,2,5,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {3,2,Integer.MAX_VALUE,3,4,Integer.MAX_VALUE},
        {Integer.MAX_VALUE,5,3,Integer.MAX_VALUE,5,3},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,4,5,Integer.MAX_VALUE,5},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,3,5,Integer.MAX_VALUE}
    
    };
    Graph graph = new Graph(vertexs, edges);
    graph.printGraph();
    graph.search();
  }
  
}

Copier après la connexion

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!