Méthode de tri rapide

HTML5 Academy-Code Craftsman : Dans les numéros précédents de "Algorithm Journey", j'ai partagé avec vous la méthode de tri par bulles et la méthode de tri par sélection. Elles ont toutes deux une complexité temporelle de O. (n^ 2) Tri "lent". Aujourd'hui, j'aimerais partager avec vous l'algorithme de tri le plus largement utilisé et le plus rapide parmi divers algorithmes de tri : le tri rapide [la complexité temporelle moyenne est O (n logn)].

Conseils 1 : Les connaissances de base de « l'algorithme » et du « tri » ont été expliquées en détail dans la précédente « Méthode de tri par sélection ». Vous pouvez cliquer sur le lien de l'article correspondant à la fin de l'article pour voir. et je ne le répéterai pas ici.

Conseil 2 : Sauf indication contraire, le tri rapide dans cet article est trié du plus petit au plus grand.

Principe du tri rapide

Le tri rapide est un tri par partition et échange. Il adopte la stratégie diviser pour régner, qui est généralement appelée la méthode diviser pour régner.

Méthode Diviser pour régner

Idée de base : décomposer le problème d'origine en plusieurs sous-problèmes plus petits mais de structures similaires au problème d'origine. Résolvez ces sous-problèmes de manière récursive, puis combinez les résultats de ces sous-problèmes avec les résultats du problème d'origine.

Principe de base

Sélectionnez n'importe quel nombre de la séquence comme "base"

Tous les nombres plus petits que la "base" sont déplacés vers la gauche de la "base" ; ; Les nombres supérieurs ou égaux à la « baseline » sont déplacés vers la droite de la « baseline »

Une fois ce déplacement terminé, la « baseline » sera au milieu des deux séquences et ne sera plus affichée. ne participe plus au tri ultérieur ;

Répétez les étapes ci-dessus pour les deux sous-séquences à gauche et à droite de la "ligne de base" jusqu'à ce qu'il ne reste qu'un seul numéro dans toutes les sous-séquences.

Illustration du principe

La séquence existante est [8, 4, 7, 2, 0, 3, 1]. Ce qui suit montre comment la trier à l'aide de la méthode de tri rapide.

Détail des étapes pour mettre en œuvre le tri rapide

Sélectionnez "baseline" et séparez-le du tableau d'origine

Obtenez l'index du première valeur de référence, puis utilisez la méthode du tableau d'épissure pour obtenir la valeur de référence.

Conseils : Dans cet exemple, la valeur d'index du benchmark = parseInt (longueur de la séquence / 2)

Conseils : La méthode d'épissage modifiera l'original tableau. Par exemple, arr = [1, 2, 3]; La valeur de l'index de base est 1, la valeur de base est 2 et le tableau d'origine devient arr = [1, 3];

Parcourez la séquence et divisez la séquence

Comparez la taille avec la "ligne de base" et divisez-la en deux sous-séquences

Les nombres plus petits que la "ligne de base" sont stockés dans le tableau leftArr, et les nombres supérieurs ou égaux au "baseline" sont stockés dans le tableau rightArr

Conseils : Bien sûr, vous pouvez également stocker le nombre inférieur ou égal à la "baseline" dans leftArr, et le nombre supérieur à la "ligne de base" dans rightArr

Puisque la séquence doit être parcourue, comparez chaque nombre avec le "benchmark", vous devez donc utiliser l'instruction for pour implémenter

appel récursif, parcourir la sous-séquence et combiner les résultats de la sous-séquence

Définir une fonction dont les paramètres formels sont utilisés pour recevoir le tableau

1. fonction quickSort(arr) { };

implémenter la séquence de traversée d'appels récursifs, utiliser la méthode de tableau concat pour combiner les résultats de la sous-séquence

Déterminer la longueur de la sous-séquence

Lors de l'appel récursif, lorsque la longueur de la sous-séquence est égale à 1 , puis arrêter l'appel récursif et renvoyer le tableau actuel.

Code complet du tri rapide

Efficacité du tri rapide

Complexité temporelle

Dans le pire des cas : la « ligne de base » sélectionnée à chaque fois est le plus petit nombre/le plus grand nombre de la séquence. Cette situation est similaire à la méthode de tri des bulles (un seul nombre [numéro de base] peut être déterminé à la fois. ), la complexité temporelle est O(n^2)

Meilleur des cas : la "ligne de base" sélectionnée à chaque fois est le nombre le plus central de la séquence (c'est la médiane, pas la position du milieu), puis le la séquence actuelle est divisée en deux sous-séquences de longueur égale à chaque fois. A ce moment, la première fois il y a deux sous-séquences n/2 et n/2, la deuxième fois il y a quatre sous-séquences n/4, n/4, n/4, n/4, et ainsi de suite, n nombres Il faut un total de fois de connexion pour terminer le tri (2^x=n, x=logn), puis la complexité est n à chaque fois. La complexité temporelle est O(n logn)

Complexité spatiale

Dans le pire des cas : n-1 appels récursifs sont requis et la complexité spatiale est O(n)

Meilleur des cas : les appels récursifs logn sont requis et la complexité spatiale est O(logn)

Stabilité de l'algorithme

Le tri rapide est un algorithme de tri instable

Par exemple : la séquence existante est [1, 0, 1, 3], et la sélection du numéro "de base" est Le deuxième 1

après le premier tour de comparaison, devient [0, 1, 1, 3], la séquence de gauche est [0] et la séquence de droite est [1, 3] (le 1 de la bonne séquence C'est le premier avant 1)

Il n'est pas difficile de constater que l'ordre des deux 1 dans la séquence originale a été détruit, et l'ordre a été modifié, ce qui est naturellement un " algorithme de tri "unstable"

À propos de O

Dans l'article précédent "Méthode de tri des bulles", nous avons expliqué en détail ce qu'est O, donc je n'entrerai pas dans les détails ici, allez simplement au photo

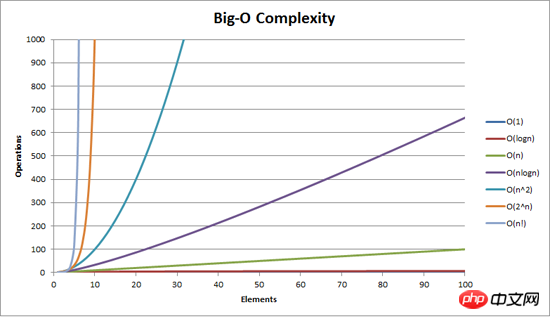
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!