
Cet article présente principalement l'utilisation par Python du modèle d'arbre de sous-ensemble de méthode de retour en arrière pour résoudre le problème de montée d'escalier. Il explique brièvement le problème de montée d'escalier et le combine avec des exemples pour fournir des compétences opérationnelles pertinentes pour le modèle d'arbre de sous-ensemble de méthode de retour en arrière de Python afin de résoudre le problème. problème de montée d'escalier.Il est obligatoire Les amis peuvent se référer à
Cet article décrit l'exemple de Python utilisant le modèle d'arborescence de sous-ensemble de méthode de retour en arrière pour résoudre le problème de montée d'escalier. Partagez-le avec tout le monde pour votre référence, les détails sont les suivants :
Problème
Un certain escalier a n marches, et chaque marche peut faites seulement 1 pas, ou 2 pas. Combien y a-t-il de façons de monter les escaliers de bas en haut ?
Analyse
Ce problème a été résolu avant d'utiliser la méthode diviser pour régner. Cependant, ici, je vais utiliser le modèle d'arborescence de sous-ensemble de retour en arrière pour le résoudre.
Faites ressortir la méthode d'analyse de l'espace élément-état : chaque étape est un élément, et le nombre d'étapes possibles [1, 2] est son espace d'état. Il n’est pas difficile de voir que les éléments ne sont pas fixes, mais que l’espace d’états est fixe.
Téléchargez le code directement.
Code
'''爬楼梯'''
n = 7 # 楼梯阶数
x = [] # 一个解(长度不固定,1-2数组,表示该步走的台阶数)
X = [] # 一组解
# 冲突检测
def conflict(k):
global n, x, X
# 部分解步的步数之和超过总台阶数
if sum(x[:k+1]) > n:
return True
return False # 无冲突
# 回溯法(递归版本)
def climb_stairs(k): # 走第k步
global n, x, X
if sum(x) == n: # 已走的所有步数之和等于楼梯总台阶数
print(x)
#X.append(x[:]) # 保存(一个解)
else:
for i in [1, 2]: # 第k步这个元素的状态空间为[1,2]
x.append(i)
if not conflict(k): # 剪枝
climb_stairs(k+1)
x.pop() # 回溯
# 测试
climb_stairs(0) # 走第0步Rendu
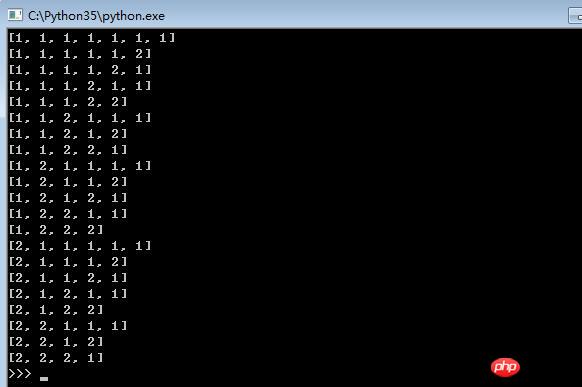
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!