
Mahout fournit des implémentations évolutives d'algorithmes classiques dans le domaine de l'apprentissage automatique, dans le but d'aider les développeurs à créer des applications intelligentes plus facilement et plus rapidement. Mahout contient de nombreuses implémentations, notamment le clustering, la classification, le filtrage des recommandations et l'exploration fréquente de sous-éléments. De plus, Mahout peut évoluer efficacement vers le cloud en utilisant la bibliothèque Apache Hadoop.

Le style d'enseignement de l'enseignant :
Les cours de l'enseignant sont simples et faciles à comprendre, de structure claire, analysés couche par couche , imbriqué et rigoureux dans l'argumentation , a une structure rigoureuse, utilise le pouvoir logique de la pensée pour attirer l'attention des élèves et utilise la raison pour contrôler le processus d'enseignement en classe. En écoutant les cours de l'enseignant, les étudiants acquièrent non seulement des connaissances, mais reçoivent également une formation à la réflexion, et sont également influencés et influencés par l'attitude académique rigoureuse de l'enseignant
Le point le plus difficile de cette vidéo est la logistique classificateur de régression_Bei Yessian Classifier_1 :
1 Contexte
Tout d'abord, au début de l'article, posons-en quelques-unes. questions , si vous pouvez répondre à ces questions, alors vous n'avez pas besoin de lire cet article, ou votre motivation pour lire est uniquement de trouver des défauts à cet article. Bien sûr, je l'accueille également. Veuillez envoyer un e-mail à "Naive Bayesian". des défauts" au 297314262 @qq.com, je lirai attentivement votre lettre.
D'ailleurs, si après avoir lu cet article, vous ne parvenez toujours pas à répondre aux questions suivantes, veuillez m'en informer par e-mail et je ferai de mon mieux pour répondre à vos doutes.
Le "naïf" dans le classificateur Naive Bayes fait spécifiquement référence aux caractéristiques de ce classificateur
Classificateur Naive Bayes et estimation du maximum de vraisemblance (MLE), maximum postérieur La relation entre la probabilité (MAP)
Classification naïve de Bayes, classification de régression logistique, modèle génératif et modèle de décision
La relation entre l'apprentissage supervisé et l'estimation bayésienne
2 Accord
Donc, ceci. l'article commence. Tout d'abord, concernant les différentes formes d'expression qui peuvent apparaître dans cet article, quelques conventions sont faites ici
Les lettres majuscules, comme X, représentent des variables aléatoires ; si X est une variable multidimensionnelle, alors l'indice ; i représente la i-ème variable de dimension, c'est-à-dire que Xi
les lettres minuscules, telles que Xij, représentent une valeur de la variable (la jème valeur de Xi)
3. apprentissage supervisé
D'accord, alors répondez d'abord à la 4ème question, comment utiliser l'estimation bayésienne pour résoudre des problèmes d'apprentissage supervisé ?
Pour l'apprentissage supervisé, notre objectif est en fait d'estimer une fonction objectif f : La variable, Y, est le résultat réel de la classification de l'échantillon. Supposons que la valeur de l'échantillon |X=xk), trouvez simplement toutes les estimations de P(X=xk|Y=yi) et toutes les estimations de P(Y=yi) basées sur l'échantillon. Le processus de classification ultérieur consiste à trouver le plus grand yi de P(Y=yi|X=xk). On peut voir que l’utilisation de l’estimation bayésienne peut résoudre le problème de l’apprentissage supervisé.
4. Caractéristiques « naïves » des classificateurs 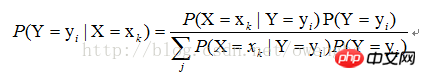
Comme mentionné ci-dessus, la solution de P(X=xk|Y=yi) peut être transformée en solution de P(X1=x1j1|Y=yi), P(X2=x2j2|Y=yi),. .. P (Xn=xnjn|Y=yi), alors comment utiliser la méthode d'estimation du maximum de vraisemblance pour trouver ces valeurs ?
Tout d'abord, nous devons comprendre ce qu'est l'estimation du maximum de vraisemblance. En fait, dans nos manuels de théorie des probabilités, les explications sur l'estimation du maximum de vraisemblance concernent toutes la résolution de problèmes d'apprentissage non supervisés. vous devez comprendre que l'utilisation de l'estimation du maximum de vraisemblance pour résoudre des problèmes d'apprentissage supervisé sous des caractéristiques naïves revient en fait à utiliser l'estimation du maximum de vraisemblance pour résoudre des problèmes d'apprentissage non supervisé dans diverses catégories de conditions.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 commande de capture de paquets Linux
commande de capture de paquets Linux
 Mot de passe par défaut du routeur
Mot de passe par défaut du routeur
 heure du système Linux
heure du système Linux
 Introduction aux composants Laravel
Introduction aux composants Laravel
 Comment utiliser la largeur de marge
Comment utiliser la largeur de marge
 Comment ignorer la connexion réseau lors de l'installation de Win11
Comment ignorer la connexion réseau lors de l'installation de Win11
 tu protèges le pilote
tu protèges le pilote
 Comment résoudre le problème selon lequel le code js ne peut pas s'exécuter après le formatage
Comment résoudre le problème selon lequel le code js ne peut pas s'exécuter après le formatage