Partagez un exemple où le nombre de chiffres dans js est trop grand, entraînant une perte de précision des paramètres.

Partagez un exemple où le nombre de chiffres dans js est trop grand, entraînant une perte de précision des paramètres

J'ai récemment rencontré un problème étrange lors du passage d'un paramètre dans. une fonction js, un bit est passé. Le nombre est relativement grand. Si vous imprimez des arguments, vous pouvez voir que les paramètres passés ont changé.

Ensuite, j'ai vérifié et j'ai découvert que cela était bien causé par la perte de précision de js. Ma solution consiste à changer le type numérique en transmission de type caractère, afin que la précision ne soit pas perdue. Comme indiqué ci-dessous :

La raison pour laquelle les nombres JS perdent en précision

L'implémentation binaire de l'ordinateur et la limite du nombre de chiffres certains nombres ne peuvent pas être représentés de manière finie. Tout comme certains nombres irrationnels ne peuvent pas être représentés de manière finie, comme pi 3,1415926..., 1,3333... etc. JS est conforme à l'IEEE La spécification 754 utilise un stockage à double précision (double précision), occupant 64 bits. Comme le montre la figure

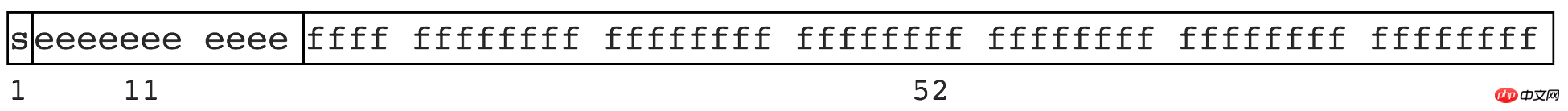
Signification

• 1 bit est utilisé pour représenter le bit de signe

• 11 bits sont utilisés pour représenter l'exposant

• 52 bits représentent la mantisse

nombre à virgule flottante, tel que

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

ne peut être utilisé que pour le moment. L'arrondi est effectué pour imiter le nombre décimal, mais le binaire n'a que deux nombres : 0 et 1, il devient donc 0 et arrondi à 1. C'est la cause première des erreurs et de la perte de précision dans certaines opérations sur les nombres à virgule flottante dans les ordinateurs.

La perte de précision des grands entiers est essentiellement la même que celle des nombres à virgule flottante. Le nombre maximum de chiffres de mantisse est de 52, donc le plus grand entier pouvant être représenté avec précision dans JS est Math.pow(2, 53), qui en décimal est 9007199254740992.

Un nombre supérieur à 9007199254740992 peut perdre en précision

9007199254740992     >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

En fait

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

Le résultat est tel qu'indiqué sur la figure

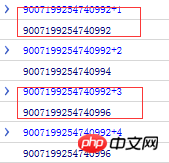
D'après ce qui précède, nous pouvons savoir que les nombres apparemment finis sont infinis dans la représentation binaire de l'ordinateur. En raison de la limitation des chiffres de stockage, il y a un « arrondi » et une perte de précision se produit.

想了解更深入的分析可以看这篇论文（又长又臭）：What Every Computer Scientist Should Know About Floating-Point Arithmetic

三、解决方案

对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。

对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!