Résumé de l'algorithme du filtre de flou gaussien Photoshop

J'ai récemment été impressionné par les recherches de certains internautes sur les filtres de flou gaussien, et je les résume ici comme suit. Le flou gaussien est une sorte de méthode de traitement de modèles d'images numériques. Son modèle est calculé sur la base d'une fonction de distribution normale bidimensionnelle (distribution gaussienne).
La distribution normale a été obtenue pour la première fois par A. Demoivre en trouvant la formule asymptotique de la distribution binomiale. C.F. Gauss l'a dérivé sous un autre angle en étudiant l'erreur de mesure. P.S. Laplace et Gauss ont étudié ses propriétés. D'où le nom de flou gaussien.

Définition de la fonction de distribution normale unidimensionnelle :

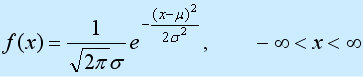
Distribution de type variables aléatoires, le premier paramètre μ est la valeur moyenne de la variable aléatoire qui suit la distribution normale, le deuxième paramètre σ2 est la variance de cette variable aléatoire, donc la distribution normale est enregistrée comme N(μ, σ2). La règle de probabilité d'une variable aléatoire qui suit une distribution normale est que la probabilité de prendre une valeur proche de μ est élevée, et la probabilité de prendre une valeur plus éloignée de μ est faible, plus σ est petit, plus la distribution est concentrée ; est proche de μ, et plus σ est grand, plus la dispersion est petite. Les caractéristiques de la fonction de densité de la distribution normale sont : elle est symétrique par rapport à μ, atteint une valeur maximale en μ, prend une valeur de 0 à l'infini positif (négatif) et a un point d'inflexion en μ±σ. Sa forme est haute au milieu et basse des deux côtés, et l'image est une courbe en forme de cloche au-dessus de l'axe des x. Lorsque μ = 0, σ2 = 1, on parle de distribution normale standard, enregistrée sous la forme N (0, 1).

La signification de deux constantes : μ-espérance, σ^2 variance.

Résolvons maintenant la première question : quel est le rayon dans le filtre de flou gaussien ? La réponse est que le rayon gaussien est σ dans la formule.

La signification de la forme et du rayon de la courbe gaussienne est indiquée dans la figure suivante (extraite de la documentation des experts du support technique dans Adobe SDK) :

> On peut voir que la courbe gaussienne Le rayon (σ) affecte la forme de la courbe. Plus le σ est petit, plus la courbe est haute et nette. Plus le σ est grand, plus la courbe est basse et douce. Pour une image bidimensionnelle, il s’agit d’une surface en forme de cloche. Plus le rayon gaussien est petit, plus la surface est haute, nette et raide ; plus le rayon gaussien est grand, plus la surface est basse et douce. Par conséquent, plus le rayon gaussien est petit, plus le flou est petit, et plus le rayon gaussien est grand, plus le flou est important. Nous verrons que ps définit la plage du rayon gaussien comme [0,1 ~ 250]. Lorsque le rayon est de 0,1, seul le pixel du milieu du modèle gaussien est calculé comme étant égal à 1, et les autres pixels sont tous = 0 (en fait approchant juste de 0), c'est-à-dire que l'image ne changera pas.

La deuxième question est la suivante : quelle est la relation entre la taille du modèle gaussien et le rayon gaussien ? C'est un malentendu qui nous a toujours troublé. Parce que notre pensée est entrée dans l’incompréhension de la réalisation physique. Dans l’implémentation physique, le modèle gaussien est limité, ce qui nous amène à ignorer la vraie réponse à cette question : le modèle gaussien est logiquement illimité. Autrement dit, le modèle gaussien est essentiellement une approximation d’une surface étendue logiquement infinie. Par conséquent, la taille du modèle doit être considérée comme infinie. C'est juste que lors du calcul, parce qu'on se rapproche de 0 au loin, on ne considère plus ces valeurs en dessous d'un certain seuil. Ce seuil est la limite du modèle.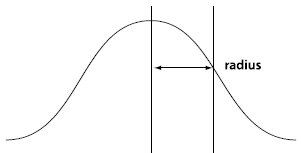

🎜>

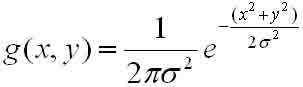
高斯模板（guass radius=0.700000）
//radius guass=0.700000
0.000000    0.000000   0.000000   0.000000   0.000000   0.000000   0.000000   0.000000   0.000000   
0,000000   0,000000   0,000001   0,0 00012    0.000033   0.000012   0.000001   0.000000   0.000000   
0.000000   0.000001 0.000093   0.001976   0.005481   0.001976   0.000093   0.000001   0.000000   
0.000000   0.000012   0.001976   0.042189   0.117046   0.042189   0.001976   0.000012   0,000000   
0.000000   0.000033   0.005481   0.117046   0,324724   0,117046   0,005481   0,0 00033   0,000000   
0,000000   0,000012   0.001976   0.042189   0.117046   0.042189   0.001976   0.000012   0.000000   
0.000000    0,000001   0,000093   0,001976   0,0 05481   0.001976   0.000093   0.000001    0.000000   
0.000000   0.000000   0.000001   0.000012   0.000033   0.000012   0.000001   0,000000   0,000000   
0,000000   0,0 00000    0,000000   0,000000   0,000000   0.000000   0.000000   0.000000   0.000000  

        整数除法形式的近似：

         1 2 1

         2 4 2    /16

         1 2 1

Vérification réelle, nous avons constaté que ce modèle 3*3 est en fait une approximation lorsque le rayon gaussien est d'environ 0,849. Lorsque r=0,849, son modèle normalisé 3*3 est (dans MATLAB, entrez h=fspecial(. 'gaussienne', 3, 0,849); pour obtenir ce modèle) :

0,062467 0,125000 0,062467 0,125000 0,250131 0,125000 0,062467 0. 125000 0.062467


Ensuite, nous pouvons utiliser imfilter dans Matlab pour effectuer un traitement de flou gaussien sur l'image :

h = fspecial('gaussian', 3, 0.849); img2 = imfilter(img, h); subplot(121), imshow(img); > subplot(122), imshow(img2); title('Après le flou gaussien')



L'effet est le suivant :

Nous pouvons l'utiliser dans Matlab comme suit : Dessiner une surface gaussienne :

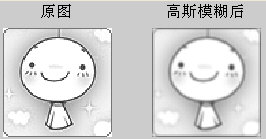Code Matlab pour dessiner une surface gaussienne surface

Mise en évidence de code réalisée par Actipro CodeHighlighter (freeware)//m.sbmmt.com/
-->#include math.h>
#include stdio.h>
#define N 3 3 🎜>/ * Taille du modèle : (2N 1) * (2N 1) */
void main(){

doublea[2*N 1] [2*N 1];  /* Modèle gaussien */
 doubler=0,6 :[ 0,1, 250] * / 
double A=1/(2 *M_PI*r*r) ;  
int i,j;
 pour( i =-1*N;iN;i ) 
pour(j=-1*N;jN;j )une[i N][j N]=A *exp((-1)*(je*i j*j)/ (2*r*r));
}

En parallèle, à titre de comparaison, nous donnons le code pour générer des modèles gaussiens dans Matlab (une partie du code pour fspecial, où p3 est le troisième paramètre qui est le rayon gaussien) :

  case 'gaussian' % Gaussian filter

     siz   = (p2-1)/2;  %注：p2即模板边长，默认值为33
     std   = p3;        %注：p3即高斯半径，默认为为0.5
     
     [x,y] = meshgrid(-siz(2):siz(2),-siz(1):siz(1));
     arg   = -(x.*x + y.*y)/(2*std*std);

     h     = exp(arg);
     h(h<eps*max(h(:))) = 0;

     sumh = sum(h(:));  %注：模板归一化
     if sumh ~= 0,
       h  = h/sumh;
     end;

Pour plus de résumé de l'algorithme des articles liés au filtre de flou gaussien Photoshop, veuillez faire attention au site Web PHP chinois !