Notations du grand O

C'est une notation qui détermine la vitesse ou la lenteur d'exécution d'un algorithme. Cette vitesse n'est pas déterminée par les secondes, mais par l'augmentation du temps d'exécution d'un algorithme à mesure que les éléments augmentent.

Big O est la relation entre le temps et la taille. Tout au long de l'article, vous verrez des graphiques avec ces mesures et vous les comprendrez mieux dans la pratique. Nous avons deux types de complexité (spatiale et temporelle).

Complexité temporelle : Détermine le temps qu'il faudra pour exécuter l'algorithme proportionnel à la taille de l'entrée.

Complexité spatiale : Détermine la quantité de mémoire qui sera allouée pour trouver l'élément dont nous avons besoin.

Pourquoi étudier cela ?

• Avec cela, vous pouvez déterminer le degré d'évolutivité d'un algorithme
• Big O traite toujours le pire des cas, exemple ci-dessous :

exemple :

• Vous avez une liste et vous souhaitez rechercher un élément mais l'élément est en fin de liste. Le pire des cas est que vous deviez effectuer autant d'opérations que possible jusqu'à ce que vous trouviez les données souhaitées.

Délais d'exécution

Tempo Constante O(1) :

• quelle que soit la taille du tableau, cela prendra toujours le même temps

exemple :

• Incrémenter ou décrémenter

function increment(value: number){
  return ++value
}

function decrement(value: number){
  return --value
}

• Prendre un article spécifique

const fruits = ["apple", "orange", "grape", "banana"]

function getItem(items: string[], index: number) {
  return items[index]
}

const item = getItem(fruits, 2)
console.log(`fruit: ${item}`) // "grape"

• Obtenir le premier élément d'un tableau

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getFirstElement(items: string[]){
 return items[0]
}

• Obtenir le dernier élément d'un tableau

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getLastElement(items: string[]){
 return items[item.length - 1]
}

let lastElement = getLastElement(animes)
console.log(`Last Element: ${lastElement}`)

Temps linéaire O(n):

• Le temps d'exécution augmente proportionnellement à la taille du tableau
• Algorithme de tri et de recherche binaire
• itération utilisant une seule boucle

exemples :

• Pour trouver le plus grand nombre dans un tableau de 10 éléments, je ferai défiler tous les éléments jusqu'à ce que je le trouve.
• Dans le pire des cas, le plus grand nombre sera le dernier.

const numbers = [0, 4, 8, 2, 37, 11, 7, 48]

function getMaxValue(items: number[]) {
    let max = numbers[0];
    for (let i=0; i <= items.length; i++){
      if(items[i] > max) {
        max = items[i]
      }
    }

    return max;
}

let maxValue = getMaxValue(numbers)

console.log(`Max Value: ${maxValue}`)

Temps logarithmique O (log n)

• La taille d'entrée augmente de n et le temps d'exécution augmente de log n, le temps augmente dans une proportion logarithmique.
• N'oubliez pas que n est le nombre d'éléments dans le tableau.
• Les entrées augmentent plus rapidement que le temps d'exécution.

exemple :

• nous effectuerons une recherche binaire dans un tableau pour trouver un élément spécifique.

const numbers = [0, 9, 24, 78, 54, 88, 92, 100, 21, 90]

function binarySearch(nums: number[], target: number) {
    let left = 0;
    let right = nums.length - 1;

    while (left <= right) {
        let middle = Math.floor((right + left) / 2);

        if (nums[middle] === target) {
            return middle;
        } else if (nums[middle] < target) {
            left = middle + 1;
        } else {
            right = middle - 1;
        }
    }

    return -1;
}

let getTarget = binarySearch(numbers, 92)
console.log(`Target: ${getTarget}`)

• Pour mieux comprendre la croissance logarithmique, regardons les choses comme suit : le tableau que nous utilisons dans l'exemple a 10 entrées, donc :

log2(10) = 3,4
log2(20) = 4,3
log2(40) = 5,3

• Le graphique ci-dessous facilitera la compréhension :

Temps linéaire/quasilinéaire O(n log n)

• Complexité temporelle d'un algorithme qui fait référence à l'exécution d'opérations logarithmiques n fois.
• Un mélange de O(log(n)) et O(n).
• Un exemple de structure est le tri par fusion.
• croît modérément.

• Une partie évolue en n et l'autre partie évolue en log(n), l'exemple ci-dessous est une fusion chanceuse :

function increment(value: number){
  return ++value
}

function decrement(value: number){
  return --value
}

Temps quadratique O(n²)

• Le temps d'exécution augmente quadratiquement à mesure que le nombre d'entrées augmente.
• Matrice de lecture.
• En gros quand 2 boucles imbriquées sont nécessaires
• Tri à bulles

exemple :

const fruits = ["apple", "orange", "grape", "banana"]

function getItem(items: string[], index: number) {
  return items[index]
}

const item = getItem(fruits, 2)
console.log(`fruit: ${item}`) // "grape"

Temps exponentiel O(2ˆn)

• Avec chaque élément inséré dans l'entrée, le temps d'exécution doublera.

• un exemple de ce code est fibonacci

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getFirstElement(items: string[]){
 return items[0]
}

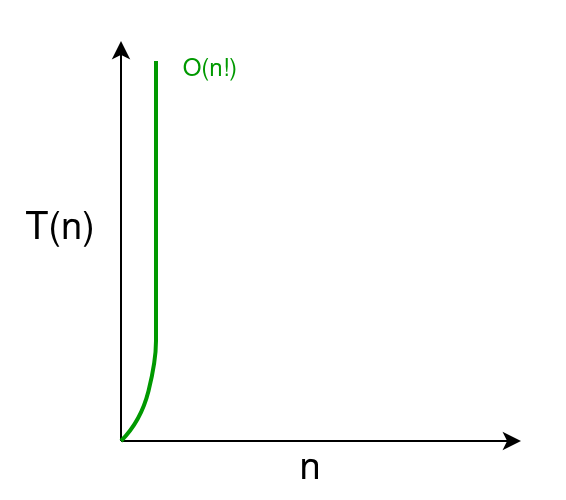
Temps factoriel O(n!)

• Le temps d'exécution augmente factoriellement en fonction de la taille de l'entrée.

exemple :

• Générer toutes les permutations dans un tableau

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getLastElement(items: string[]){
 return items[item.length - 1]
}

let lastElement = getLastElement(animes)
console.log(`Last Element: ${lastElement}`)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!