Construire un système de navigation pour drones en utilisant matplotlib et l'algorithme A*

Vous êtes-vous déjà demandé comment les drones naviguent dans des environnements complexes ? Dans ce blog, nous allons créer un système de navigation simple pour drones en utilisant Python, Matplotlib et l'algorithme A*. À la fin, vous disposerez d'un système fonctionnel qui visualise un drone résolvant un labyrinthe !

Ce que vous apprendrez

1. Terminologies de base de l'IA telles que « agent » et « environnement ».
2. Comment créer et visualiser un labyrinthe avec Python.
3. Comment fonctionne l'algorithme A* pour résoudre les problèmes de navigation.
4. Comment mettre en œuvre et visualiser la trajectoire du drone.

Présentation

Pour construire notre système de navigation par drone, nous avons besoin des éléments suivants :

1. Un agent :Le drone ?.
2. Un chemin : Un labyrinthe 2D dans lequel le drone naviguera ?️.
3. Un algorithme de recherche : L'algorithme A* ⭐.

Mais d’abord, passons rapidement en revue quelques termes de base de l’IA pour ceux qui sont nouveaux.

Termes clés de l'IA

• Agent : Une entité (comme notre drone) qui perçoit son environnement (labyrinthe) et prend des mesures pour atteindre un objectif (atteindre la fin du labyrinthe).
• Environnement : Le monde dans lequel l'agent évolue, ici représenté sous la forme d'un labyrinthe 2D.
• Heuristique : Une règle empirique ou une estimation utilisée pour guider la recherche (comme mesurer la distance jusqu'à l'objectif).

La conception du système

Notre drone naviguera dans un labyrinthe 2D. Le labyrinthe sera composé de :

• Murs (régions infranchissables représentées par des 1).
• Chemins (espaces ouverts représentés par des 0).

Les objectifs du drone :

1. Éviter les murs.?
2. Atteindre le bout du chemin.?

Voici à quoi ressemble le labyrinthe :

Étape 1 : Configuration du labyrinthe

Importer les bibliothèques requises

Tout d'abord, installez et importez les bibliothèques requises :

import matplotlib.pyplot as plt
import numpy as np
import random
import math
from heapq import heappop, heappush

Définir les dimensions du labyrinthe

Définissons la taille du labyrinthe :
python
LARGEUR, HAUTEUR = 22, 22

Définir les directions et les poids

Dans la navigation réelle, les déplacements dans différentes directions peuvent avoir des coûts variables. Par exemple, se déplacer vers le nord peut être plus difficile que se déplacer vers l'est.

DIRECTIONAL_WEIGHTS = {'N': 1.2, 'S': 1.0, 'E': 1.5, 'W': 1.3}
DIRECTIONS = {'N': (-1, 0), 'S': (1, 0), 'E': (0, 1), 'W': (0, -1)}

Initialiser la grille du labyrinthe

On commence par une grille remplie de murs (1s) :

import matplotlib.pyplot as plt
import numpy as np
import random
import math
from heapq import heappop, heappush

Le numpy. La fonction ones() est utilisée pour créer un nouveau tableau de forme et de type donnés, rempli de uns... utile pour initialiser un tableau avec des valeurs par défaut.

Étape 2 : sculpter le labyrinthe

Définissons maintenant une fonction qui "taillera" des chemins dans votre labyrinthe qui est actuellement initialisé avec uniquement des murs

DIRECTIONAL_WEIGHTS = {'N': 1.2, 'S': 1.0, 'E': 1.5, 'W': 1.3}
DIRECTIONS = {'N': (-1, 0), 'S': (1, 0), 'E': (0, 1), 'W': (0, -1)}

Définir les points de début et de fin

maze = np.ones((2 * WIDTH + 1, 2 * HEIGHT + 1), dtype=int)

Étape 3 : Visualiser le labyrinthe

Utilisez Matplotlib pour afficher le labyrinthe :

def carve(x, y):
    maze[2 * x + 1, 2 * y + 1] = 0  # Mark current cell as a path
    directions = list(DIRECTIONS.items())
    random.shuffle(directions)  # Randomize directions

    for _, (dx, dy) in directions:
        nx, ny = x + dx, y + dy
        if 0 <= nx < WIDTH and 0 <= ny < HEIGHT and maze[2 * nx + 1, 2 * ny + 1] == 1:
            maze[2 * x + 1 + dx, 2 * y + 1 + dy] = 0
            carve(nx, ny)

carve(0, 0)  # Start carving from the top-left corner

Étape 4 : Résoudre le labyrinthe avec A*

L'algorithme A* trouve le chemin le plus court dans un labyrinthe pondéré en utilisant une combinaison de coût de chemin et d'heuristique.

Définir l'heuristique

Nous utilisons la Distance euclidienne comme heuristique :

start = (1, 1)
end = (2 * WIDTH - 1, 2 * HEIGHT - 1)
maze[start] = 0
maze[end] = 0

Une* Implémentation d'un Algorithme

fig, ax = plt.subplots(figsize=(8, 6))
ax.imshow(maze, cmap='binary', interpolation='nearest')
ax.set_title("2D Maze")
plt.show()

Étape 5 : Visualiser la solution

Nous avons le labyrinthe mais vous ne pouvez pas encore voir la trajectoire du drone.
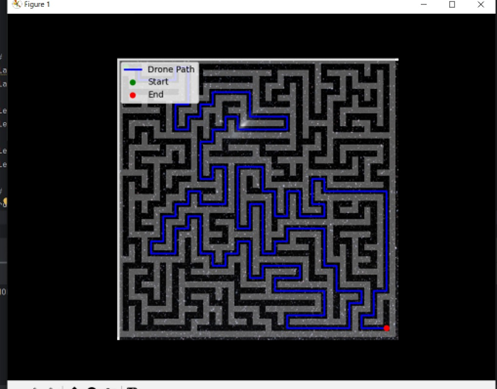
Visualisons la trajectoire du drone :

def heuristic(a, b):
    return math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)

Conclusion

Félicitations ! ? Vous avez construit un système de navigation par drone fonctionnel qui :

• Génère un labyrinthe 2D.
• Le résout en utilisant l'algorithme A*.
• Visualise le chemin le plus court.

Prochaines étapes

1. Expérimentez avec différentes tailles et poids de labyrinthe.
2. Essayez d'autres heuristiques comme la distance de Manhattan.
3. Visualisez un labyrinthe 3D pour plus de complexité !

N'hésitez pas à partager vos résultats ou à poser des questions dans les commentaires ci-dessous.
Vers l'infini et au-delà ?

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!