Modifier les poids des bords du graphique

2699. Modifier les poids des bords du graphique

Difficulté :Difficile

Sujets :Graphique, tas (file d'attente prioritaire), chemin le plus court

Vous recevez unconnecté pondéré non orientécontenant n nœuds étiquetés de 0 à n - 1, et un tableau d'entiers edge où edge[i] = [a_i, b_i, w_i] indique qu'il y a une arête entre les nœuds a_iet b_ide poids w_i.

Certaines arêtes ont un poids de -1 (w_i= -1), tandis que d'autres ont un poidspositif(w_i> 0) .

Votre tâche consiste à modifiertoutes les arêtesavec un poids de -1 en leur attribuant desvaleurs entières positivesdans la plage [1, 2 * 10⁹] afin que ladistance la plus courteentre les nœuds source et destination devienne égale à une cible entière. S'il y aplusieurs modificationsqui rendent la distance la plus courte entre la source et la destination égale à la cible, chacune d'entre elles sera considérée comme correcte.

Renvoyerun tableau contenant toutes les arêtes (même celles non modifiées) dans n'importe quel ordre s'il est possible de rendre la distance la plus courte de la source à la destination égale à la cible, ou untableau videsi c'est impossible.

Remarque :Vous n'êtes pas autorisé à modifier les poids des arêtes avec des poids initiaux positifs.

Exemple 1 :

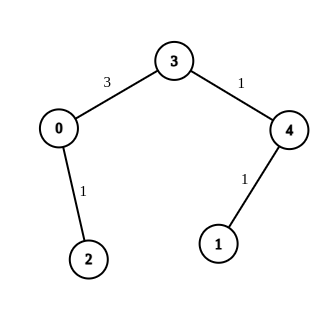
• Entrée :n = 5, bords = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ], source = 0, destination = 1, cible = 5
• Sortie :[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
• Explication :Le graphique ci-dessus montre une possible modification des bords, rendant la distance de 0 à 1 égale à 5.

Exemple 2 :

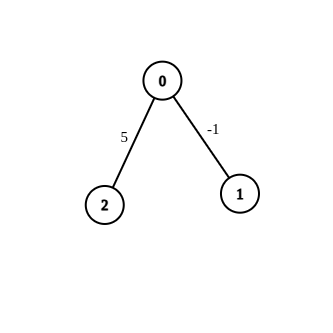
• Entrée :n = 3, bords = [[0,1,-1],[0,2,5]], source = 0, destination = 2, cible = 6
• Sortie :[]
• Explication :Le graphique ci-dessus contient les arêtes initiales. Il n'est pas possible de rendre la distance de 0 à 2 égale à 6 en modifiant l'arête avec le poids -1. Ainsi, un tableau vide est renvoyé.

Exemple 3 :

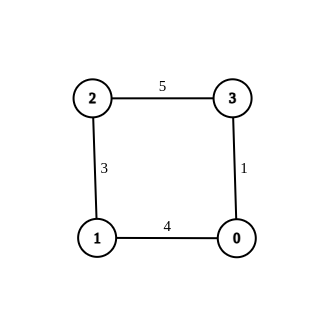
• Entrée :n = 4, bords = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, cible = 6
• Sortie :[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
• Explication :Le graphique ci-dessus montre un graphique modifié ayant la distance la plus courte de 0 à 2 comme 6.

Contraintes :

• 1 <= n <= 100
• 1 <= bords.longueur <= n * (n - 1) / 2
• bords[i].length == 3
• 0 <= a_i, b_i< n
• w_i= -1 ou 1 <= w_i<= 10⁷
• a_i!= b_i
• 0 <= source, destination < n
• source != destination
• 1 <= cible <= 10⁹
• Le graphique est connecté et il n'y a pas de boucles automatiques ni d'arêtes répétées

Indice :

1. Tout d'abord, vérifiez qu'il est réellement possible de rendre le chemin le plus court de la source à la destination égal à la cible.
2. Si le chemin le plus court de la source à la destination sans les bords à modifier, est inférieur à la cible, alors ce n'est pas possible.
3. Si le chemin le plus court de la source à la destination incluant les arêtes à modifier et en leur attribuant un poids temporaire de 1, est supérieur à la cible, alors ce n'est pas non plus possible.
4. Supposons que nous puissions trouver une arête modifiable (u, v) telle que la longueur du chemin le plus court de la source à u (dis1) plus la longueur du chemin le plus court de v à la destination (dis2) soit inférieure à la cible (dis1 + dis2 < target), alors nous pouvons changer son poids en « target - dis1 - dis2 ».
5. Pour toutes les autres arêtes qui ont encore le poids « -1 », changez les poids en nombre suffisamment grand (cible, cible + 1 ou 200000000 etc.).

Solution :

On peut décomposer la démarche comme suit :

Approche:

1. Vérification initiale avec les poids existants :

   • Tout d'abord, nous calculons le chemin le plus court de la source à la destination en utilisant uniquement les arêtes de poids positif, en ignorant les arêtes de poids -1.
   • Si cette distance est déjà supérieure à la cible, alors il est impossible de modifier les arêtes -1 pour atteindre la cible, nous renvoyons donc un tableau vide.

2. Attribution temporaire du poids 1 :

   • Ensuite, attribuez un poids temporaire de 1 à toutes les arêtes de poids -1 et recalculez le chemin le plus court.
   • Si ce chemin le plus court est toujours supérieur à la cible, alors il est impossible d'atteindre la cible, nous renvoyons donc un tableau vide.

3. Modifier les poids de bord spécifiques :

   • Parcourez les bords avec un poids -1 et identifiez les bords qui peuvent être ajustés pour correspondre exactement à la distance cible. Cela se fait en ajustant le poids d'un bord de telle sorte que les distances combinées des chemins menant à et depuis ce bord donnent la distance cible exacte.
   • Pour toutes les arêtes -1 restantes, attribuez un poids suffisamment grand (par exemple, 2 * 10^9) pour vous assurer qu'elles n'ont pas d'impact sur le chemin le plus court.

4. Retourner les bords modifiés :

   • Enfin, renvoie la liste des arêtes modifiée.

Implémentons cette solution en PHP :2699. Modifier les poids des bords du graphique

        
Explication:
        

         
La fonction dijkstra calcule le chemin le plus court depuis la source vers tous les autres nœuds.
         
Nous calculons initialement le chemin le plus court en ignorant les arêtes -1.
         
Si le chemin sans arêtes -1 est inférieur à la cible, la fonction renvoie un tableau vide, indiquant qu'il est impossible d'ajuster les poids pour atteindre la cible.
         
Sinon, nous définissons temporairement toutes les arêtes -1 sur 1 et vérifions si le chemin le plus court dépasse la cible.
         
Si c'est le cas, il est encore une fois impossible d'atteindre la cible, et nous renvoyons un tableau vide.
         
Nous modifions ensuite les poids des arêtes -1 de manière stratégique pour obtenir le chemin le plus court souhaité de la cible exacte.
        
Cette approche vérifie et ajuste efficacement les poids des bords, garantissant que la distance cible est respectée si possible.
Liens de contact
Si vous avez trouvé cette série utile, pensez à donner une étoile auréférentielsur GitHub ou à partager la publication sur vos réseaux sociaux préférés ?. Votre soutien signifierait beaucoup pour moi !
Si vous souhaitez du contenu plus utile comme celui-ci, n'hésitez pas à me suivre :
        

         
LinkedIn
         
GitHub
        
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!