Une avancée significative dans l'hypothèse de Riemann ! Tao Zhexuan recommande fortement les nouveaux articles du MIT et d'Oxford, et le lauréat de la médaille Fields, âgé de 37 ans, a participé

Récemment, l'hypothèse de Riemann, connue comme l'un des sept problèmes majeurs du millénaire, a atteint une nouvelle avancée.

L'hypothèse de Riemann est un problème non résolu très important en mathématiques, lié aux propriétés précises de la distribution des nombres premiers (les nombres premiers sont ces nombres qui ne peuvent être divisés que par 1 et eux-mêmes, ils jouent un rôle fondamental dans rôle de la théorie des nombres).

Dans la littérature mathématique actuelle, il existe plus d'un millier de propositions mathématiques basées sur l'établissement de l'hypothèse de Riemann (ou sa forme généralisée). En d’autres termes, une fois que l’hypothèse de Riemann et sa forme généralisée seront prouvées, ces plus d’un millier de propositions seront établies sous forme de théorèmes, qui auront un impact profond sur le domaine des mathématiques et si l’hypothèse de Riemann s’avère fausse, alors parmi eux ; ces propositions qui en font partie perdront également leur validité.

La nouvelle avancée vient d'un article du professeur de mathématiques du MIT Larry Guth et du professeur de l'Institut de mathématiques de l'Université d'Oxford et lauréat de la médaille Fields James Maynard. Le mathématicien Terence Tao, qui a recommandé l'article, a déclaré qu'ils constituaient la première amélioration substantielle par rapport à la liaison classique d'Ingham de 1940 sur les zéros de la fonction zêta riemannienne (et, plus généralement, sur le contrôle des grandes valeurs de diverses séries de Dirichlet). Auparavant, le principe d'Ingham, né il y a plus de 80 ans, empêchait les mathématiciens de faire beaucoup de choses en théorie analytique des nombres en raison du manque d'améliorations.

Cependant, Tao Zhexuan a également déclaré que bien qu'il s'agisse d'une avancée significative, elle est encore loin de résoudre complètement l'hypothèse de Riemann, elle doit donc être considérée de manière rationnelle.

Quelle est l'hypothèse de Riemann ?

L'hypothèse de Riemann ou hypothèse de Riemann a été proposée par le mathématicien allemand Bernhard Riemann en 1859. Cette conjecture est étroitement liée à la distribution des nombres premiers et son contenu principal implique les zéros non triviaux de la fonction Zeta de Riemann.

                                                                                                                                                                                                                         ^{Bernhard Riemann, Source : fact.net/}

Le contenu de l'hypothèse de Riemann ne peut pas être décrit par des mathématiques complètement élémentaires. En gros, il s'agit d'une conjecture pour une fonction variable complexe appelée fonction zêta de Riemann (c'est-à-dire une fonction dans laquelle la variable et la valeur de la fonction peuvent prendre des valeurs dans le domaine complexe). La fonction zêta de Riemann, comme beaucoup d'autres fonctions, a une valeur nulle en certains points. Ces points sont appelés points zéro de la fonction zêta de Riemann. Parmi ces zéros, il existe des zéros non triviaux particulièrement importants appelés fonction zêta de Riemann. Ce que suppose l'hypothèse de Riemann, c'est que tous les points zéro non triviaux sont distribués sur une ligne droite spéciale appelée « ligne critique » (citée sur le blog de l'écrivain scientifique populaire Lu Changhai).

La fonction Riemann ζ est définie comme :

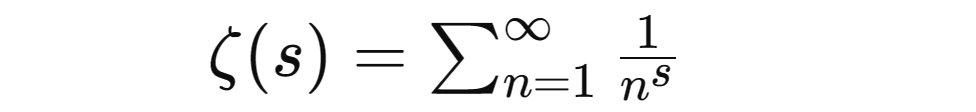
L'hypothèse de Riemann soutient que la partie réelle de tous les zéros non triviaux de la fonction ζ est 1/2. Cela signifie que si ζ(s)=0 et s est un zéro non trivial (c'est-à-dire que s n'est même pas négatif), alors la partie réelle de s devrait être 1/2.

L'hypothèse de Riemann est le problème mathématique le plus important et le plus attendu au monde aujourd'hui. Si la conjecture est vraie, la distribution des nombres premiers parmi les nombres naturels peut être décrite avec précision, et elle aura une large application et influence dans la résolution de la théorie des nombres, de l'analyse complexe et d'autres branches des mathématiques.

Jusqu'à présent, 165 ans se sont écoulés depuis que l'hypothèse de Riemann a été proposée. De nombreuses études ont tenté de prouver l’hypothèse de Riemann, mais elles n’ont toutes abouti à rien.

Tentatives pour résoudre l'hypothèse de Riemann

Depuis que l'hypothèse de Riemann a été proposée, de nombreux mathématiciens ont commencé un voyage d'exploration de la preuve.

En 1896, les mathématiciens français Jacques Adamard et Charles Jean de la Vallée-Poussin ont prouvé indépendamment qu'il n'y a pas de point zéro sur une ligne droite. Avec d'autres propriétés que Riemann avait prouvées pour les zéros non triviaux, cela montre que tous les zéros non triviaux doivent se trouver sur des régions. Il s’agit d’une étape cruciale dans la première preuve complète du théorème des nombres premiers.

En 1900, David Hilbert, mathématicien allemand et l'un des pères des mathématiques modernes, a inclus l'hypothèse de Riemann dans ses célèbres 23 questions, et avec l'hypothèse de Goldbach, ils ont formé la liste de Hilbert Question n° 8. Dans le même temps, l’hypothèse de Riemann est également le seul problème de Hilbert à être inclus dans le prix du millénaire du Clay Mathematics Institute.

En 1914, le mathématicien britannique Godfrey Harold Hardy a prouvé qu'il existe une infinité de points zéro sur la ligne droite 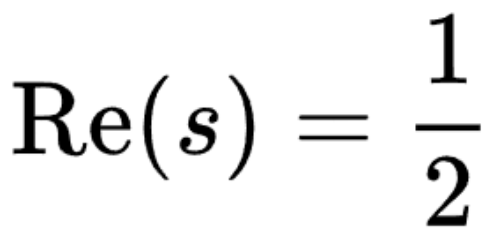. Plus tard, les travaux de Hardy et du mathématicien britannique John Unther Littlewood en 1921 et de Selberg en 1942 (théorème de la ligne critique) consistèrent à calculer la densité moyenne des points zéro sur la ligne critique .

Jusqu’à ces dernières années, les tentatives visant à prouver l’hypothèse de Riemann ont souvent fait sensation.

En septembre 2018, un discours sans précédent à Heidelberg a fait exploser le cercle des mathématiques La preuve de l’hypothèse de Riemann par Sir Atiyah, 89 ans, a attiré l’attention du monde entier. Sous les projecteurs, Sir Atiyah a passé 45 minutes à présenter au monde la preuve de cette conjecture mathématique qui a une histoire de plus de 150 ans.

Mais la preuve de Sir Atiyah n’est que la page suivante du PPT. Une telle preuve ne semble pas convaincante. Lorsqu'on lui a demandé s'il avait résolu l'hypothèse de Riemann, il a répondu : « Cela dépend de votre logique. J'ai prouvé l'hypothèse de Riemann originale, à moins que vous ne soyez le genre de mathématicien qui n'accepte pas la preuve par contradiction. n’a pas résolu tous les problèmes, et il y en aura beaucoup dans le futur. Il n’a fait que le premier pas (le premier pas est la solution).

Malheureusement, Sir Atiyah est décédé en janvier 2019.

Maintenant, quelqu'un d'autre a contesté l'hypothèse de Riemann.

Ce que Guth et Maynard ont fait

Concernant la nouvelle percée de Guth et Maynard, la célèbre mathématicienne Teresa Tao a commenté : « Guth et Maynard ont fait des progrès importants dans l'étude de l'hypothèse de Riemann, même s'ils sont encore loin d'avoir résolu cette longue question. -problème permanent. Les problèmes de mathématiques ont encore un long chemin à parcourir. mathématicien Albert Ingham. Des améliorations substantielles furent apportées vers 1940 sur les bornes classiques sur les zéros de la fonction zêta riemannienne (et plus généralement sur les grandes valeurs régissant diverses séries de Dirichlet).

En 1940, le mathématicien Albert Ingham a proposé une borne décrivant ces points zéro, qui constituait la base des recherches théoriques de l'époque. Cependant, jusqu'aux travaux de Guth et Maynard, cette limite avait à peine été affinée. Les recherches de Guth et Maynard ont non seulement amélioré cette limite d'Ingham, mais leur méthode a fourni de nouveaux outils et perspectives pour traiter les grandes valeurs des séries de Dirichlet, qui sont importantes dans de nombreux problèmes de théorie des nombres et d'analyse.

Cet article prouve une nouvelle limite sur la fréquence des grandes valeurs des polynômes de Dirichlet. Cela fournit une estimation améliorée pour un polynôme de Dirichlet de longueur N, avec des valeurs proches de

. De plus, l'étude dérive une estimation de densité du point zéro

et une expression asymptotique pour les nombres premiers sur de courts intervalles de longueur

.

Tao Zhexuan lui-même a donné quelques explications sur cette recherche d'un point de vue mathématique. Soit ?(σ,?) le nombre de zéros de la fonction de Riemann ζ où la partie réelle est au moins σ et la partie imaginaire est au plus T. L'hypothèse de Riemann nous dit que N (σ,?) disparaîtra pour tout σ>1/2, mais cette hypothèse ne peut pas encore être prouvée. Mais comme deuxième meilleure option, les mathématiciens peuvent prouver une estimation de densité du point zéro, qui est une limite supérieure non triviale sur ?(σ,?) .

Il s'avère que σ=3/4 est une valeur clé. En 1940, Ingham a dérivé la limite ?(3/4,?)≪?(3/5+?(1)).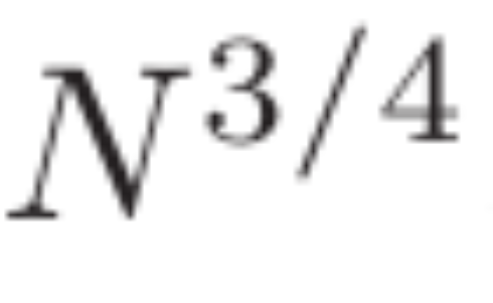

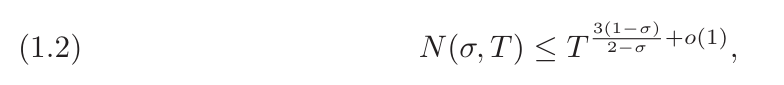
Au cours des quatre-vingts années suivantes, les améliorations apportées à cette limite n'étaient que des améliorations mineures de l'erreur ?(1). Cela limite les chercheurs à mener des recherches plus approfondies en théorie analytique des nombres : par exemple, afin d'obtenir un bon théorème des nombres premiers dans presque tous les intervalles courts de la forme (?,?+?^?), les gens ont longtemps été limités à ?>1/6 de portée, le principal obstacle est le manque d'amélioration des limites d'Ingham.

Guth et Maynard ont finalement amélioré la limite d'Ingham de 3/5=0,6 à 13/25=0,52. Cela a produit de nombreuses améliorations correspondantes dans la théorie analytique des nombres. Par exemple, les chercheurs peuvent prouver l’étendue du théorème des nombres premiers dans presque n’importe quel intervalle court, maintenant de θ>1/6=0,166… à θ>2/15=0,133…

À propos de l'auteur

Larry Guth est professeur de mathématiques Claude E. Shannon au MIT depuis juillet 2019 et a été élu MacVicar Fellow en 2021.

Il a obtenu son doctorat du MIT en 2005 sous la direction de Tom Mrowka. Il a ensuite effectué un postdoctorat à l'Université Stanford, occupé un poste de professeur junior à l'Université de Toronto et, en 2011, il a été nommé professeur au Courant Institute. Il a ensuite rejoint le département de mathématiques du MIT en tant que professeur en 2012.

Les intérêts de recherche de Guth sont la géométrie métrique, l’analyse harmonique et les combinaisons de valeurs extrêmes. La géométrie métrique fait référence à l'étude des inégalités impliquant la longueur, la surface et le volume. Quelques exemples majeurs sont les inégalités isopérimétriques et les inégalités de contraction. Les inégalités de contraction étaient au centre du travail de Guth, et un autre objectif était de trouver des liens entre les inégalités géométriques et la topologie.

Récemment, Guth est engagé dans des recherches sur l'analyse harmonique et la combinatoire. De nombreux travaux sont liés au problème de Kakeya, un problème non résolu en géométrie euclidienne, aux estimations de type restreint dans l'analyse de Fourier et aux estimations des taux d'occurrence de lignes en combinatoire extrême.

                                                                                  ^{Né en 1987, un mathématicien britannique dont le domaine de recherche est la théorie analytique des nombres, en particulier la théorie des nombres premiers.}

Certains des problèmes les plus connus de la théorie des nombres concernent la distribution des nombres premiers. Alors que la distribution à grande échelle des nombres premiers suit les théorèmes de la théorie des nombres (plus précisément l'hypothèse de Riemann), de nombreux problèmes naturels doivent être traités à des échelles courtes (ou clairsemées).

James Maynard a obtenu des résultats importants sur la conjecture des jumeaux premiers en 2013. Il a prouvé qu'il existe une infinité de paires de nombres premiers avec des intervalles inférieurs à 600. Ce résultat est plus petit que les 70 millions d'intervalles de Zhang Yitang. Bien que son article ait été publié six mois plus tard que Zhang Yitang, ses résultats ont été très appréciés parmi les experts en théorie des nombres.

Tao Zhexuan a commenté : "Pour être honnête, sa façon de décrire est en fait plus propre que la mienne... Il s'avère que sa déclaration est légèrement plus forte."

La méthode de Maynard est à la fois élégante et puissante, d'une manière choquante. franchit les limites de la théorie du dépistage. Et dans une direction apparemment opposée, il a poursuivi en montrant que parfois les nombres premiers sont beaucoup plus rares que la moyenne, un célèbre problème d'Erdős qui n'avait pas fait de progrès substantiels depuis des décennies.

Maynard a également réalisé des travaux fondamentaux dans le domaine de l'approximation diophantienne, résolvant la conjecture de Duffin-Schaeffer avec Koukoulopoulos, professeur de mathématiques à l'Université de Montréal. Cette conjecture, proposée en 1941, peut être considérée comme la généralisation finale du théorème de Khintchine, qui décrit comment un nombre réel typique peut être approché par un nombre rationnel.

En 2022, Maynard a reçu la médaille Fields pour ses contributions à la théorie analytique des nombres. La médaille Fields est la récompense la plus prestigieuse en mathématiques et est souvent considérée comme le prix Nobel de mathématiques. James Maynard est honoré pour ses contributions à la théorie analytique des nombres, qui ont conduit à des avancées significatives dans la compréhension de la structure des nombres premiers et de l'approximation diophantienne.

En 2023, il a remporté un autre prix Nouveaux Horizons en mathématiques.

J'attends avec impatience que les deux mathématiciens progressent davantage sur des problèmes mondiaux tels que l'hypothèse de Riemann.

Lien de référence :

https://www.jiqizhixin.com/articles/2019-01-12

^{https://www.zhihu.com/tardis/zm/ art/557594612}

^{https://news.mit.edu/2014/profile-larry-guth-0527}

^{https://mathstodon.xyz/@tao/112557248794707738}

^{https://zh.wikipedia.org/wiki/% E9% BB%8E% EBC%9% EBC%8% 9C% E6%83%B3}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!