
MLP (Multi-Layer Perceptron) has been used for decades. Is there really no other choice?
Multilayer Perceptron (MLP), also known as fully connected feedforwardNeural Network, is the basic building block of today's deep learning models.
The importance of MLPs cannot be overstated as they are the default method for approximating nonlinear functions in machine learning.
However, is MLP the best nonlinear regressor we can build? Although MLPs are widely used, they have significant drawbacks. For example, in Transformer models, MLPs consume almost all non-embedded parameters and are generally less interpretable relative to attention layers without post-processing analysis tools.
So, is there an alternative to MLP?
Today, KAN appeared.

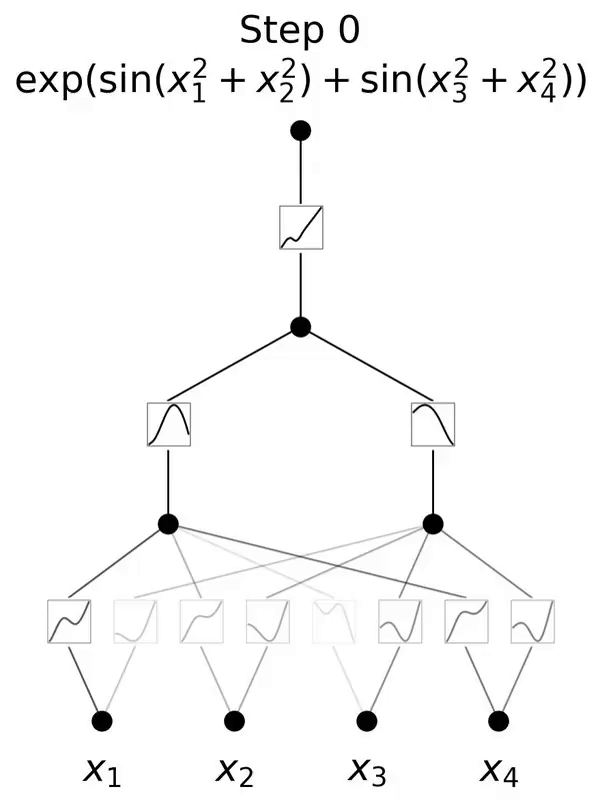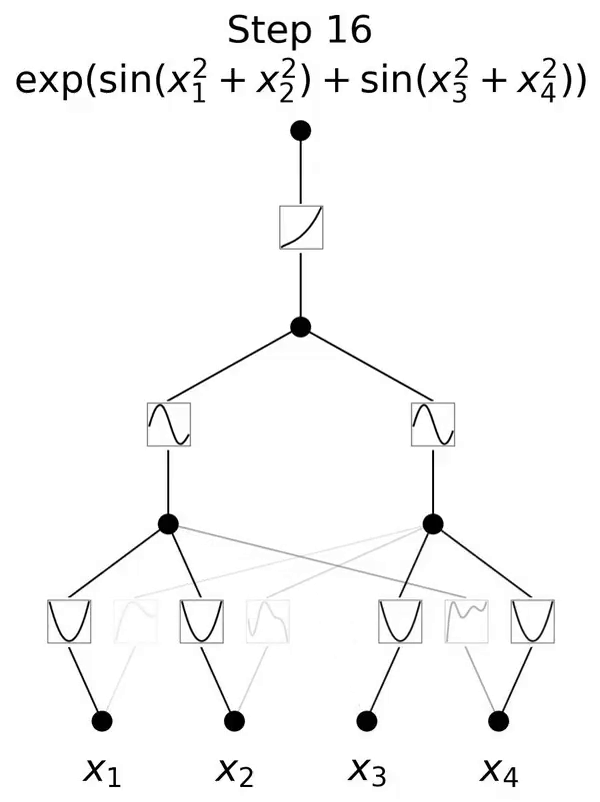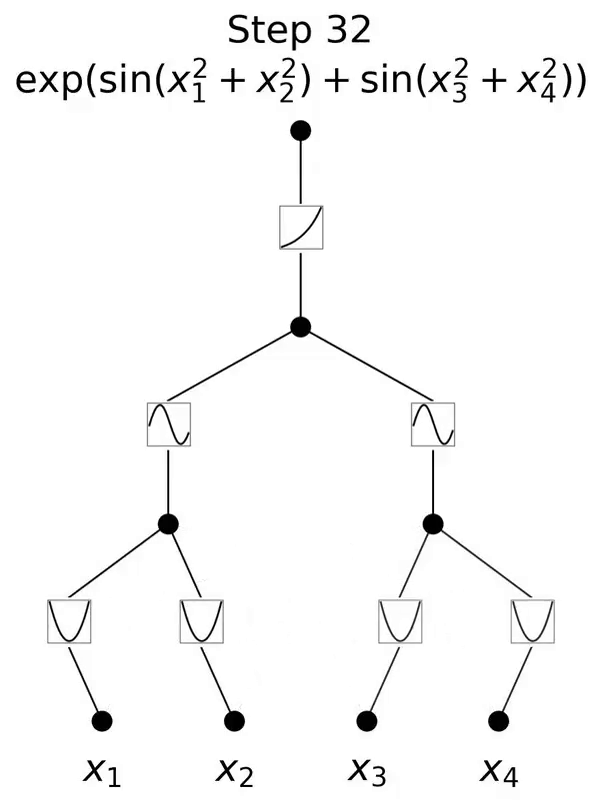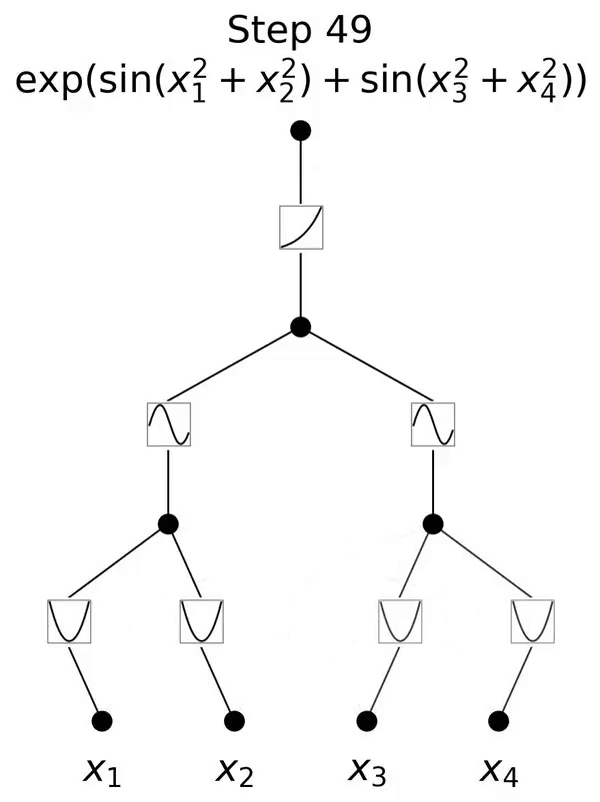

This is a network inspired by the Kolmogorov-Arnold representation theorem.
Link: https://arxiv.org/pdf/2404.19756
Github: https://github.com/KindXiaoming/pykan
Once the study was released, it attracted widespread attention and discussion on foreign social platforms.
Some netizens said that Kolmogorov discovered the multi-layer neural network as early as 1957, much earlier than Rumerhart, Hinton and William's 1986 paper, but he was ignored by the West.

# Some netizens also said that the release of this paper means that the death knell of deep learning has sounded.

Some netizens wondered whether this research would be as disruptive as the Transformer paper.

But some authors stated that they did the same thing based on the improved Kolmogrov-Gabor technique in 2018-19.
Next, let’s take a look at what this paper is about?
Paper Overview
This paper proposes a promising alternative to multilayer perceptrons (MLP) called Kolmogorov-Arnold Networks (KAN). The design of MLP is inspired by the universal approximation theorem, while the design of KAN is inspired by the Kolmogorov-Arnold representation theorem. Similar to MLP, KAN has a fully connected structure. Whereas MLP places fixed activation functions on nodes (neurons), KAN places learnable activation functions on edges (weights), as shown in Figure 0.1. Therefore, KAN has no linear weight matrix at all: each weight parameter is replaced by a learnable one-dimensional function parameterized as a spline. KAN's nodes simply sum the incoming signals without applying any nonlinear transformation.
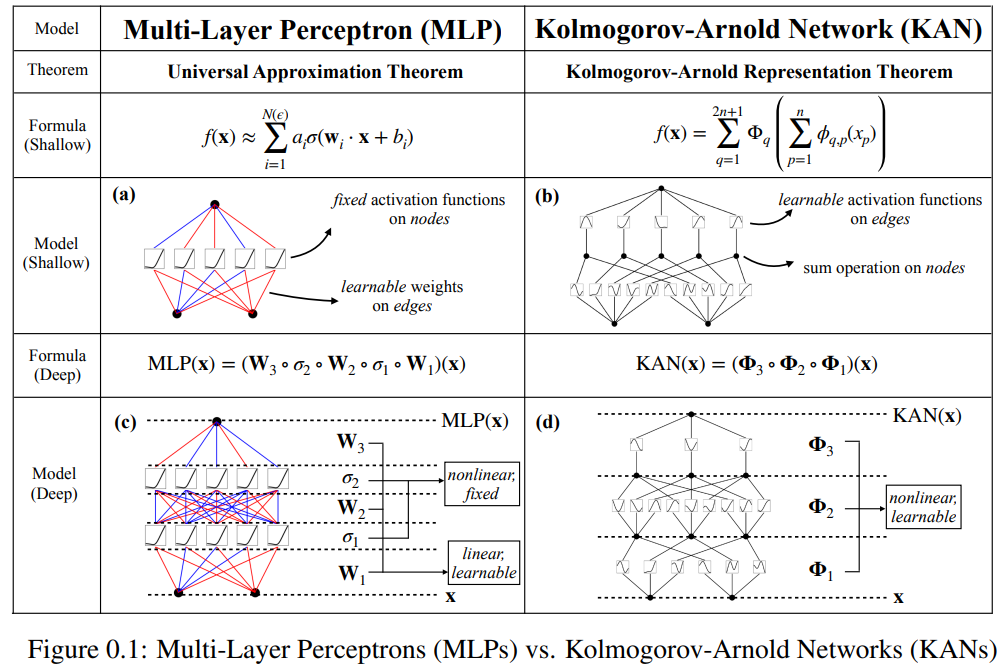
Some people may worry that the cost of KAN is too high because the weight parameters of each MLP become the spline function of KAN. However, KAN allows for a much smaller computational graph than MLP. For example, the researchers showed that PED solution: a KAN with two layers of width 10 is 100 times more accurate than an MLP with four layers of width 100 (MSE are 10^-7 and 10^-5 respectively), and is also better in parameter efficiency. Improved by 100 times (number of parameters are 10^2 and 10^4 respectively).
The possibility of using the Kolmogorov-Arnold representation theorem to construct neural networks has been studied. However, most work is stuck on the original depth 2, width (2n 1) representation, and there is no opportunity to leverage more modern techniques (e.g., backpropagation) to train the network. The contribution of this article is to generalize the original Kolmogorov-Arnold representation to arbitrary width and depth, making it revitalized in today's deep learning field, while using a large number of empirical experiments to highlight its potential role as a basic model of "AI science". This is due to the accuracy and interpretability of KAN.
Although KAN has good mathematical explanation capabilities, in fact they are just a combination of splines and MLP, taking advantage of the advantages of both and avoiding the disadvantages. Splines are highly accurate on low-dimensional functions, easy to adjust locally, and can switch between different resolutions. However, since splines cannot exploit combinatorial structures, they suffer from serious COD problems. MLPs, on the other hand, are less affected by COD due to their feature learning capabilities, but are not as accurate as splines in low-dimensional spaces because they cannot optimize univariate functions.
In order to accurately learn a function, the model should not only learn the combinatorial structure (external degrees of freedom), but also approximate the univariate function (internal degrees of freedom) well. KANs are such models because they resemble MLPs externally and splines internally. As a result, KAN can not only learn features (thanks to their external similarity to MLPs) but also optimize these learned features to very high accuracy (thanks to their internal similarity to splines).
For example, for a high-dimensional function:
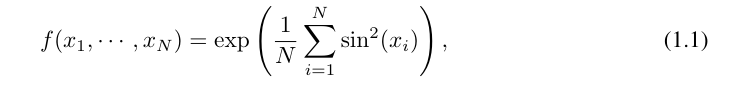
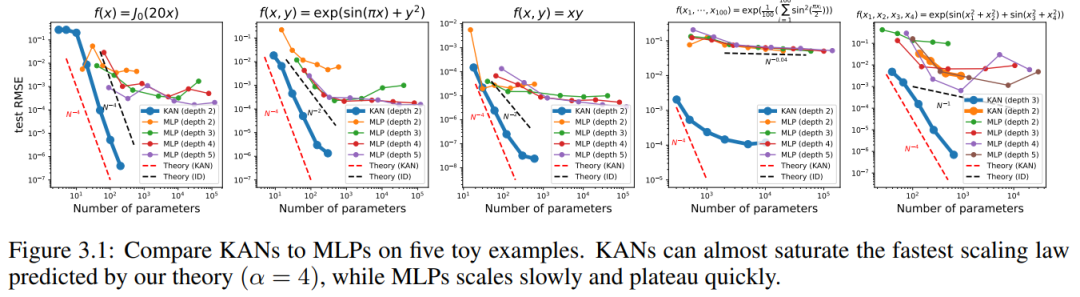
#When N is large, the spline will fail due to COD; although it is possible for MLP to learn generalized additive structure, but using activation functions such as ReLU to approximate exponential and sine functions is very inefficient. In contrast, KAN is able to learn combinatorial structures and univariate functions very well, thus outperforming MLP by a large margin (see Figure 3.1).
In this paper, the researchers showed a large number of experimental values, which reflect KAN's significant improvement in MLP in terms of accuracy and interpretability. The structure of the paper is shown in Figure 2.1 below. The code is available at https://github.com/KindXiaoming/pykan and can also be installed via pip install pykan.
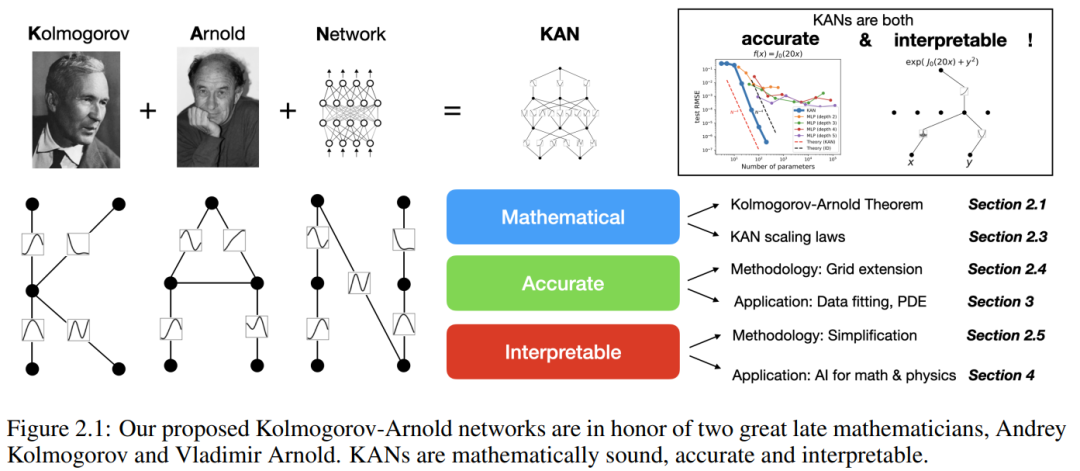
Kolmogorov-Arnold Network (KAN)
Kolmogorov-Arnold Representation Theorem
Vladimir Arnold and Andrey Kolmogorov proved that if f is a multi-variable continuous function over a bounded domain, then f can be written as a finite combination of a uni-variable continuous function and the binary addition operation. More specifically, for a smooth function f : [0, 1]^n → R, it can be expressed as:
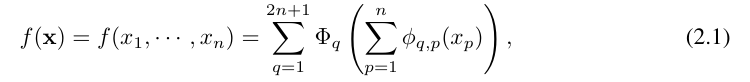 where
where 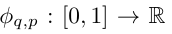 and
and 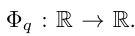
In a sense, they showed that the only true multivariable function is addition, since all other functions can be represented by univariable functions and summations. One might think that this is good news for machine learning: learning a high-dimensional function boils down to learning a one-dimensional function in polynomial quantities. However, these one-dimensional functions may be non-smooth or even fractal and thus may not be learned in practice. The Kolmogorov-Arnold representation theorem is therefore essentially a death sentence in machine learning, considered theoretically correct but practically useless.
However, researchers are more optimistic about the practicality of the Kolmogorov-Arnold theorem in machine learning. First, there is no need to stick to the original equation, which has only two layers of nonlinearity and a small number of terms (2n 1) in a hidden layer: the researcher will generalize the network to arbitrary widths and depths. Second, most functions in science and daily life are usually smooth and have sparse combinatorial structures, which may facilitate smooth Kolmogorov-Arnold representations.
KAN Architecture
Suppose there is a supervised learning task consisting of input and output pairs {x_i, y_i}. The researcher hopes to find a function f such that y_i ≈ f (x_i) for all data points. Equation (2.1) means that if the appropriate single-variable functions 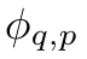 and
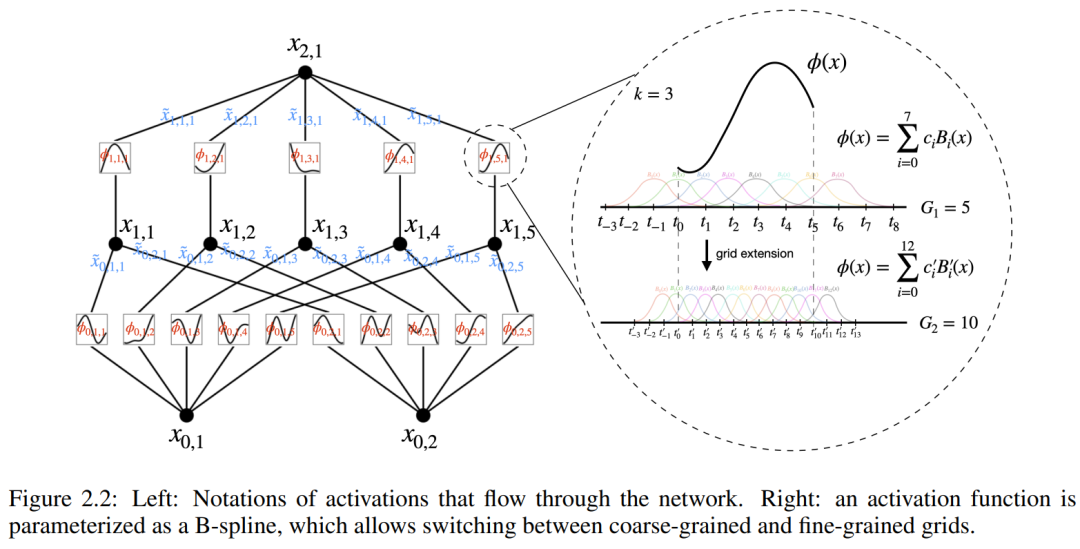
and 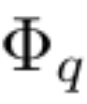 can be found, then the task is accomplished. This inspires researchers to design a neural network that explicitly parameterizes equation (2.1). Since all functions to be learned are univariate functions, the researcher parameterizes each one-dimensional function as a B-spline curve with learnable coefficients of local B-spline basis functions (see the right side of Figure 2.2). We now have a prototype of KAN, whose computational graph is fully specified by equation (2.1) and illustrated in Figure 0.1(b) (input dimension n = 2), which looks like a two-layer neural network with activation Functions are placed on edges instead of nodes (a simple summation is performed on nodes), and the middle layer width is 2n 1.
can be found, then the task is accomplished. This inspires researchers to design a neural network that explicitly parameterizes equation (2.1). Since all functions to be learned are univariate functions, the researcher parameterizes each one-dimensional function as a B-spline curve with learnable coefficients of local B-spline basis functions (see the right side of Figure 2.2). We now have a prototype of KAN, whose computational graph is fully specified by equation (2.1) and illustrated in Figure 0.1(b) (input dimension n = 2), which looks like a two-layer neural network with activation Functions are placed on edges instead of nodes (a simple summation is performed on nodes), and the middle layer width is 2n 1.
As mentioned before, in practice such networks are considered too simple to allow any function to be approximated with smoothing splines with arbitrary accuracy. Therefore, researchers generalize KAN to wider and deeper networks. Since the Kolmogorov-Arnold representation corresponds to a two-layer KAN, it is not clear how to make the KAN deeper.
The breakthrough point is that the researchers noticed the analogy between MLP and KAN. In MLP, once a layer (consisting of linear transformations and nonlinearities) is defined, more layers can be stacked to make the network deeper. To build a deep KAN, you should first answer: "What is a KAN layer?" Researchers found that a KAN layer with n_in-dimensional input and n_out-dimensional output can be defined as a one-dimensional function matrix.
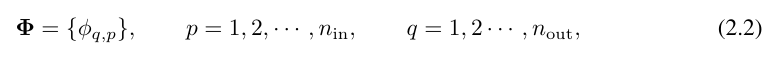
where function  has trainable parameters as described below. In the Kolmogorov-Arnold theorem, the inner functions form a KAN layer with n_in = n and n_out = 2n 1 and the outer functions form a KAN layer with n_in = 2n 1 and n_out = 1. Therefore, the Kolmogorov-Arnold representation in equation (2.1) is simply a combination of two KAN layers. Now, having a deeper Kolmogorov-Arnold representation means: just stack more KAN layers!
has trainable parameters as described below. In the Kolmogorov-Arnold theorem, the inner functions form a KAN layer with n_in = n and n_out = 2n 1 and the outer functions form a KAN layer with n_in = 2n 1 and n_out = 1. Therefore, the Kolmogorov-Arnold representation in equation (2.1) is simply a combination of two KAN layers. Now, having a deeper Kolmogorov-Arnold representation means: just stack more KAN layers!
Further understanding requires the introduction of some symbols. You can refer to Figure 2.2 (left) for specific examples and intuitive understanding. The shape of KAN is represented by an integer array:

#where n_i is the number of nodes in the i-th layer of the computational graph. Here, (l, i) represents the i-th neuron of the l-th layer, and x_l,i represents the activation value of the (l, i) neuron. Between the l-th layer and the l-th layer, there are n_l*n_l 1 activation functions: the activation function connecting (l, j) and (l 1, i) is expressed as
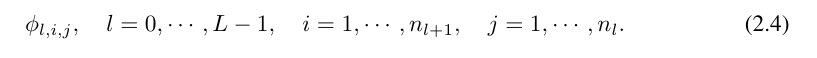
The pre-activation value of function ϕ_l,i,j is simply expressed as x_l,i; the post-activation value of ϕ_l,i,j is 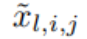 ≡ ϕ_l,i,j (x_l,i). The activation value of the (l 1, j) neuron is the sum of all incoming activation values:
≡ ϕ_l,i,j (x_l,i). The activation value of the (l 1, j) neuron is the sum of all incoming activation values:
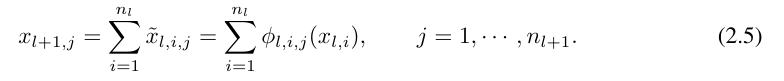
It is expressed in matrix form as follows:

Where, Φ_l is the function matrix corresponding to the l-th KAN layer. A general KAN network is a combination of L layers: given an input vector x_0 ∈ R^n0, the output of KAN is
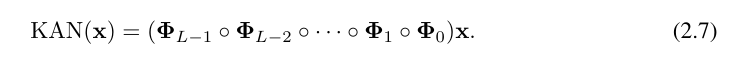
The above equation can also be written similar to the equation ( 2.1) situation, assuming the output dimension n_L = 1, and define f (x) ≡ KAN (x):
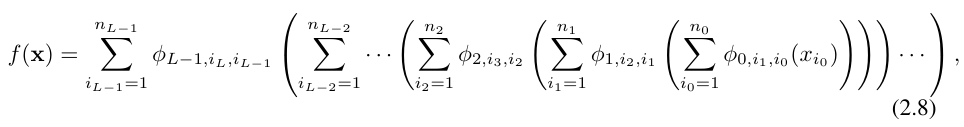
This is quite tedious to write. In contrast, the researchers' abstraction of the KAN layer and its visualization are more concise and intuitive. The original Kolmogorov-Arnold representation (2.1) corresponds to a 2-layer KAN of shape [n, 2n 1, 1]. Note that all operations are differentiable, so KAN can be trained with backpropagation. For comparison, MLP can be written as the interweaving of affine transformation W and nonlinear σ:
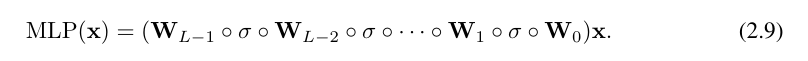
It is obvious that MLP processes linear transformation and nonlinearity as W and σ respectively, while KAN processes them together as Φ. In Figure 0.1 (c) and (d), the researchers show three-layer MLP and three-layer KAN to illustrate the difference between them.
Accuracy of KAN
In the paper, the authors also demonstrated that in various tasks (regression and partial differential equation solving), KAN is better at representing functions than MLP is more efficient. And they also show that KAN can naturally function in continuous learning without catastrophic forgetting.
toy Dataset
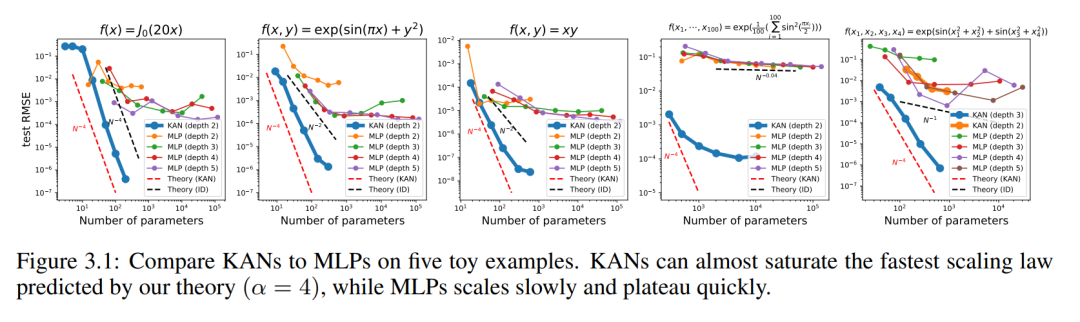
We plot the test RMSE of KAN and MLP as a function of the number of parameters in Figure 3.1, showing that KAN scales better than MLP Curves, especially in high-dimensional examples. For comparison, the authors plot the line predicted according to their KAN theory, as the red dashed line (α = k 1 = 4), and the line predicted according to Sharma & Kaplan [17], as the black dashed line (α = (k 1)/ d = 4/d). KAN can almost fill the steeper red line, while MLP even struggles to converge at the slower black line's rate and quickly reaches a plateau. The authors also note that for the last example, the 2-layer KAN performs much worse than the 3-layer KAN (shape [4, 2, 2, 1]). This highlights that deeper KANs are more expressive, and the same is true for MLPs: deeper MLPs are more expressive than shallower MLPs.
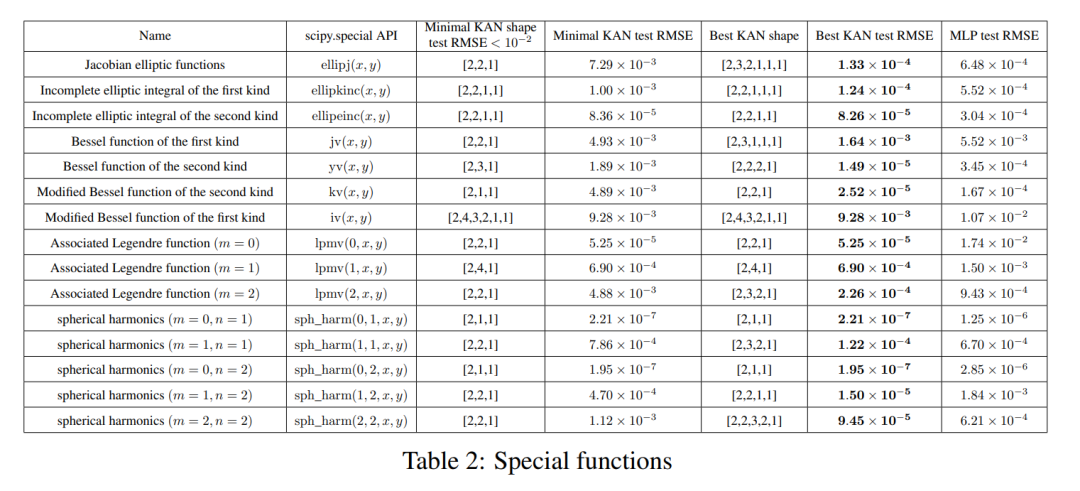
Special functions
We show the following two points in this part:
(1) Find special (Approximately) compact KA representations of functions are possible, which reveals new mathematical properties of special functions from the perspective of Kolmogorov-Arnold representations.
(2) KAN is more efficient and accurate than MLP in representing special functions.
For each data set and each model family (KAN or MLP), the authors plotted the Pareto frontier on the number of parameters and the RMSE plane, as shown in Figure 3.2.
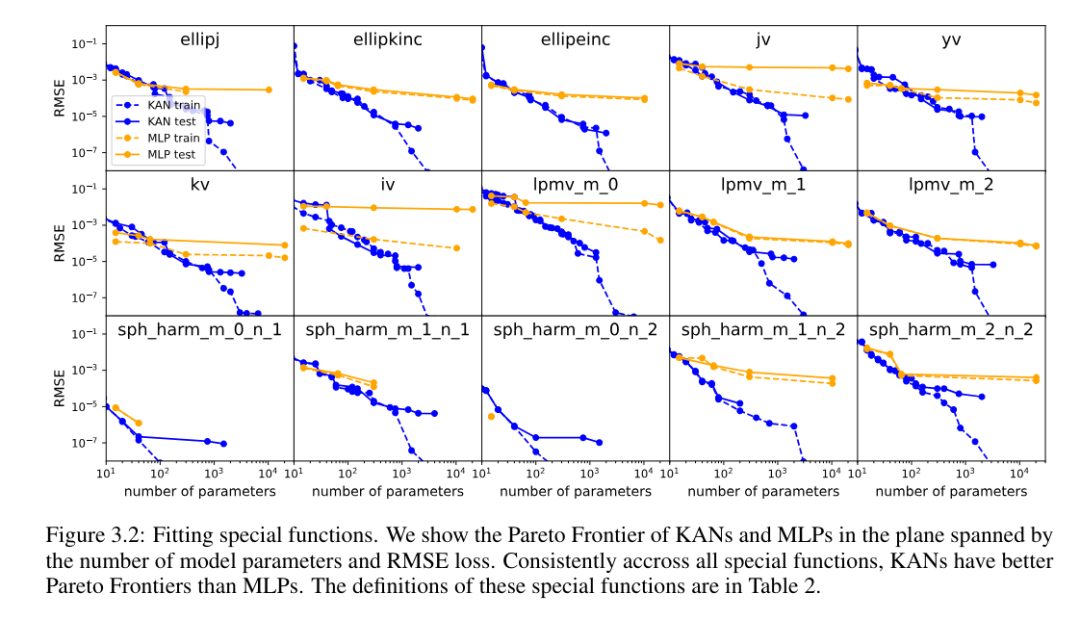
#The performance of KAN is consistently better than MLP, that is, with the same number of parameters, KAN is able to achieve lower training/test losses than MLP. Furthermore, the authors report in Table 2 the (surprisingly compact) shape of the KAN for the special function they automatically discovered. On the one hand, it is interesting to explain mathematically the meaning of these compact representations. On the other hand, these compact representations mean that it is possible to decompose a high-dimensional lookup table into several one-dimensional lookup tables, which can potentially save a lot of memory without the (almost negligible) overhead of performing some addition operations at inference time. .
Feynman Data Set
The setting in the previous section is that we clearly know the "real" KAN shape. The setup in the previous section is that we obviously don't know the "real" KAN shape. This section studies an intermediate setting: given the structure of the dataset, we might build KANs by hand, but we are not sure whether they are optimal.
For each hyperparameter combination, the author tried 3 random seeds. For each dataset (equation) and each method, they report in Table 3 the results of the best model (minimum KAN shape or lowest test loss) at random seeds and depths.
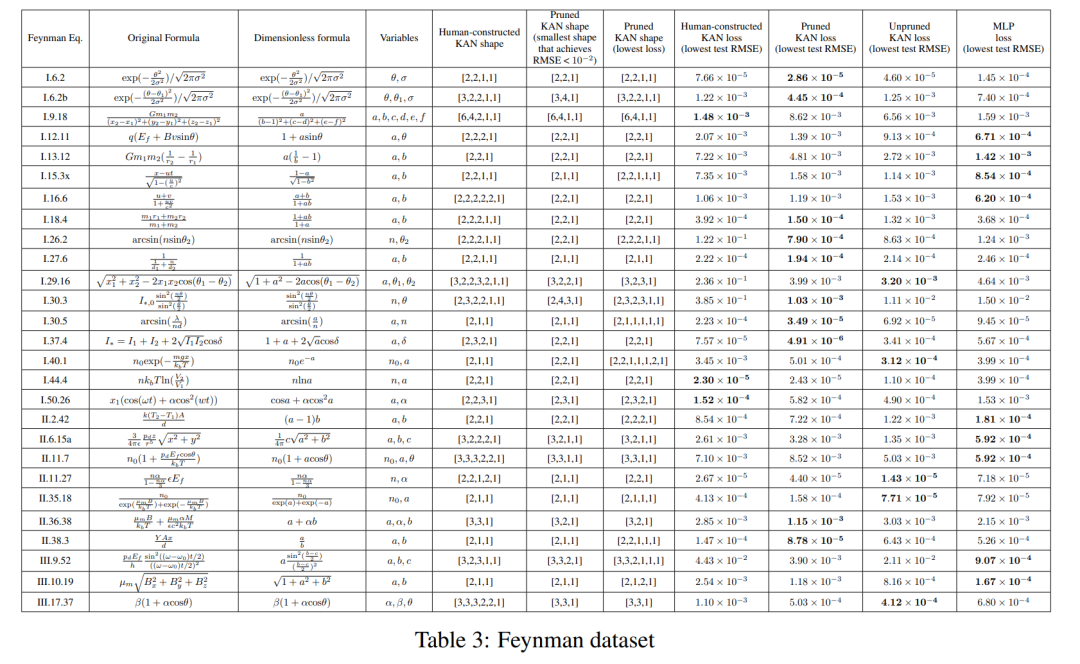
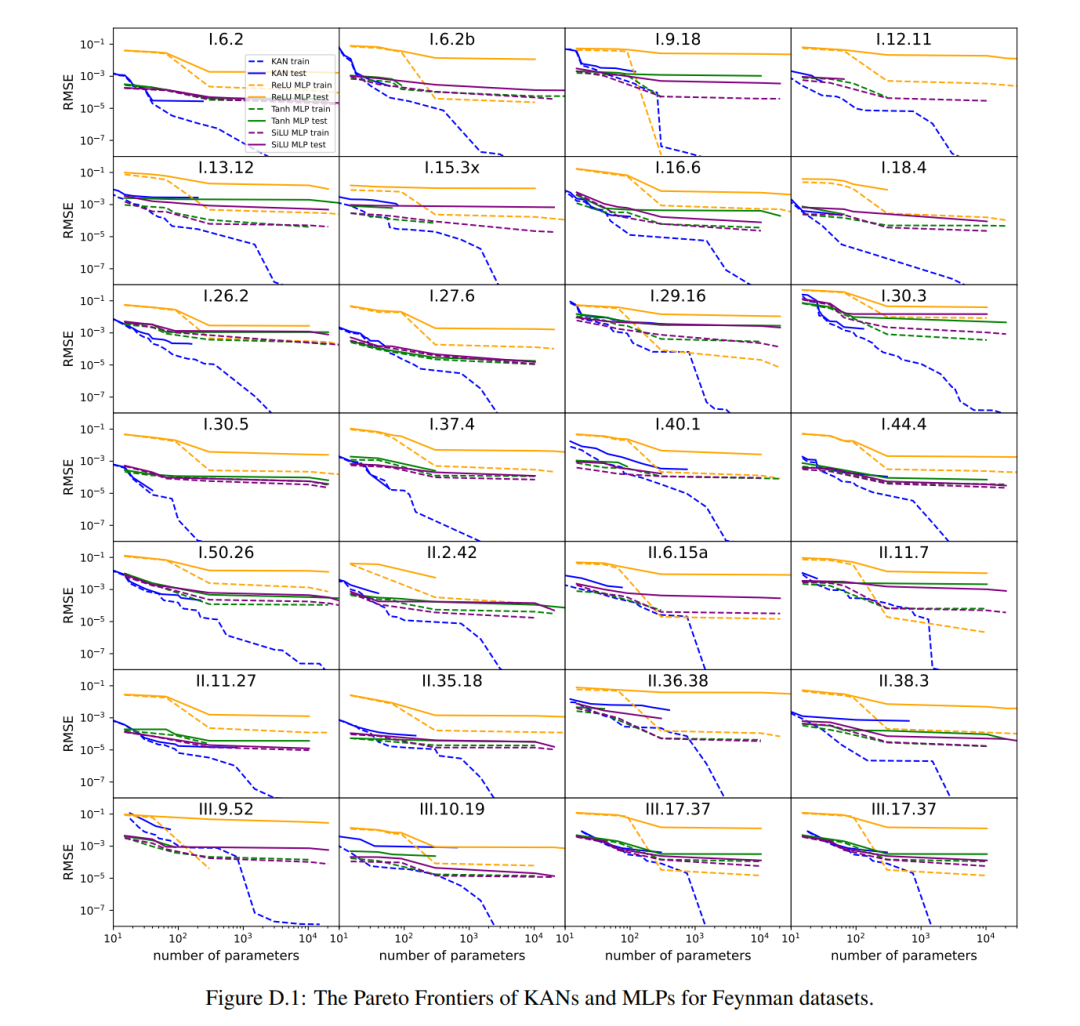
They found that MLP and KAN performed comparably on average. For each dataset and each model family (KAN or MLP), the authors plotted the Pareto frontier on the plane formed by the number of parameters and the RMSE loss, as shown in Figure D.1. They speculate that the Feynman data set is too simple to allow further improvements by KAN, in the sense that variable dependencies are often smooth or monotonic, in contrast to the complexity of special functions, which often exhibit oscillatory behavior.
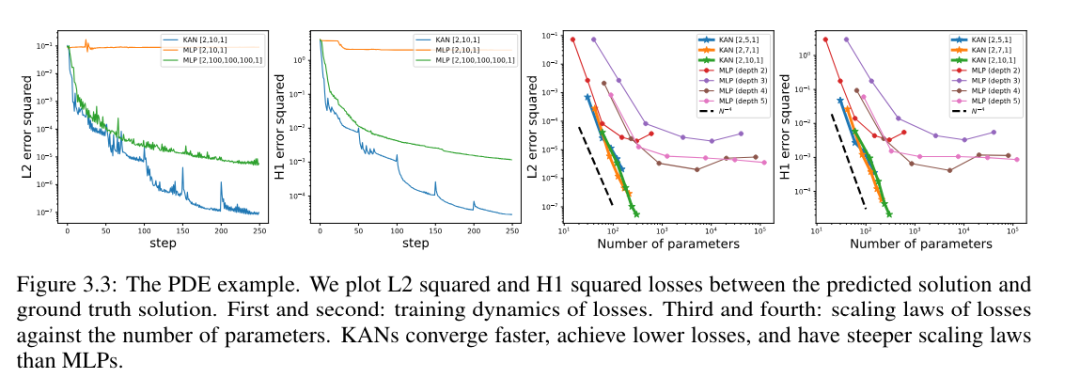
Solving Partial Differential Equations
The authors compared KAN and MLP architectures using the same hyperparameters. They measured the error in L^2 norm and energy (H^1) norm, and observed that KAN achieved better scaling law and smaller error while using a smaller network and fewer parameters, See Figure 3.3. Therefore, they speculated that KAN might have the potential to serve as a good neural network representation for partial differential equation (PDE) model reduction.
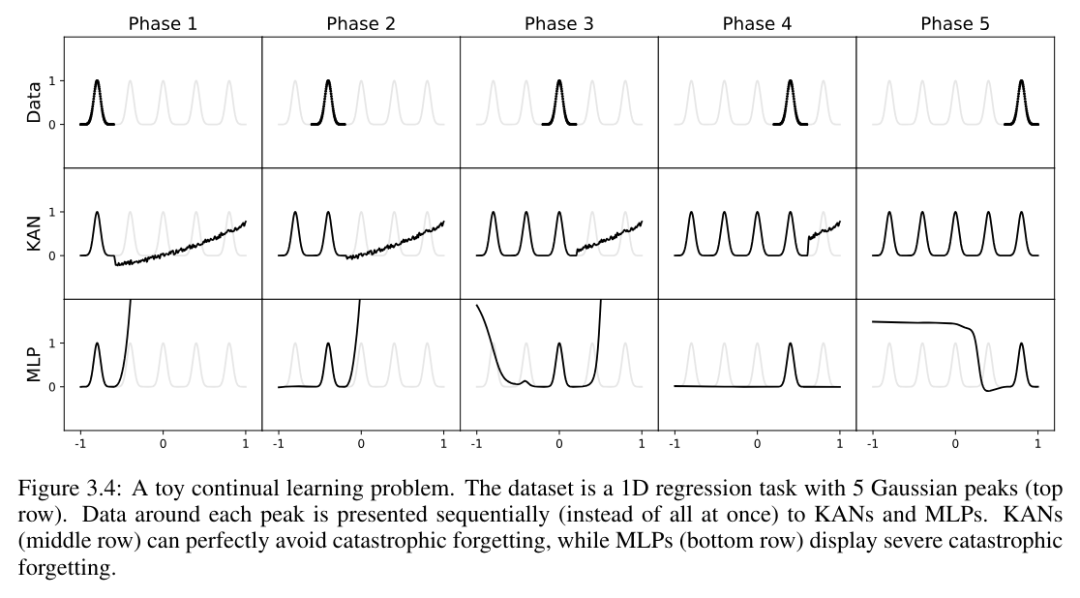
Continuous Learning
The authors show that KAN has local plasticity and can avoid catastrophic forgetting by exploiting the locality of spline . The idea is simple: since the spline basis is local, a sample will only affect a few nearby spline coefficients, while leaving the distant coefficients unchanged (this is what we want, since the distant regions may already store the coefficients we want retained information). In contrast, since MLP usually uses global activation functions such as ReLU/Tanh/SiLU, etc., any local changes may propagate uncontrollably to distant regions, destroying the information stored there.
The author uses a simple example to verify this intuition. A one-dimensional regression task consists of 5 Gaussian peaks. The data around each peak is presented sequentially (rather than all at once), as shown in the top row of Figure 3.4, presented separately to KAN and MLP. The prediction results of KAN and MLP after each training stage are shown in the middle and bottom rows, respectively. As expected, KAN only reconstructs regions where data exists at the current stage, leaving previous regions unchanged. In contrast, MLP reconstructs the entire region after seeing a new data sample, leading to catastrophic forgetting.
KAN is interpretable
In Chapter 4 of the article, the author shows that KAN is interpretable due to the technology, interpretable and interactive. They wanted to test the application of KAN not only on synthesis tasks (Sects. 4.1 and 4.2), but also in real-life scientific research. They show that KANs are able to (re)discover complex relationships in junction theory (Section 4.3) and phase transition boundaries in condensed matter physics (Section 4.4). Due to its accuracy and interpretability, KAN has the potential to become a foundational model in AI Science.
Discussion
In the paper, the author discusses the limitations and future development directions of KAN from the perspectives of mathematical foundations, algorithms and applications.
Mathematical aspects: Although the author has performed a preliminary mathematical analysis of KANs (Theorem 2.1), their mathematical understanding is still very limited. The Kolmogorov-Arnold representation theorem has been thoroughly studied mathematically, but it corresponds to a KAN of shape [n, 2n 1, 1], which is a very restricted subclass of KAN. Does the empirical success on deeper KANs imply something mathematically fundamental? An attractive generalized Kolmogorov-Arnold theorem could define "deeper" Kolmogorov-Arnold representations beyond the combination of two layers, and potentially relate the smoothness of the activation function to depth. Suppose there are functions that cannot be represented smoothly in the original (depth 2) Kolmogorov-Arnold representation, but may be represented smoothly at depth 3 or deeper. Can we use this concept of "Kolmogorov-Arnold depth" to characterize function classes?
In terms of algorithms, they discussed the following points:
Accuracy. There are multiple options in architecture design and training that have not been fully investigated, so there may be alternatives to further improve accuracy. For example, the spline activation function might be replaced by radial basis functions or other local kernel functions. Adaptive grid strategies can be used.
efficiency. One of the main reasons why KAN is slow is because different activation functions cannot take advantage of batch computation (large amounts of data passed through the same function). In fact, we can interpolate between MLP (all activation functions are the same) and KAN (all activation functions are different) by grouping the activation functions into groups ("multiples"), where members of the group share the same activation function.
Hybrid of KAN and MLP. Compared with MLP, KAN has two main differences:
(i) The activation function is located on the edges instead of nodes;
(ii ) The activation function is learnable rather than fixed.
Which change better explains the advantages of KAN? The authors present their preliminary results in Appendix B, where they study a model with (ii), i.e. the activation function is learnable (like KAN), but without (i), i.e. the activation function is located at the nodes (Like an MLP). Additionally, one can build another model whose activation function is fixed (like MLP) but located on the edges (like KAN).
Adaptability. Due to the inherent locality of spline basis functions, we can introduce adaptivity in the design and training of KANs to improve accuracy and efficiency: see [93, 94] for multi-level training ideas such as multigrid methods, or Domain-dependent basis functions like multiscale methods in [95].
Applications: The authors have presented some preliminary evidence that KAN is more effective than MLP in science-related tasks, such as fitting physical equations and solving PDEs. They anticipate that KAN may also be promising in solving the Navier-Stokes equations, density functional theory, or any other task that can be formulated as a regression or PDE solution. They also hope to apply KAN to tasks related to machine learning, which will require integrating KAN into current architectures, such as transformers - one can propose "kansformers" to replace MLPs with KAN in transformers.
KAN as Language Models for AI Science: Large language models are transformative because they are useful to anyone who can use natural language. The language of science is functions. KANs are composed of interpretable functions, so when a human user stares at a KAN, it's like communicating with it using functional language. This paragraph is intended to emphasize the AI-scientist collaboration paradigm rather than the specific tool KAN. Just like people use different languages to communicate, the authors foresee that in the future KAN will be just one of the languages of AI science, although KAN will be one of the first languages that enables AI and humans to communicate. However, thanks to the enablement of KAN, the AI-scientist collaboration paradigm has never been easier and more convenient, making us rethink how we want to approach AI science: Do we want AI scientists, or do we want AI that helps scientists? An inherent difficulty for scientists in (fully automated) AI is the difficulty of quantifying human preferences, which would codify human preferences into AI goals. In fact, scientists in different fields may have different feelings about which functions are simple or explainable. Therefore, it is preferable for scientists to have an AI that can speak the language of science (functions) and can easily interact with the inductive biases of individual scientists to suit a specific scientific domain.
Key question: Use KAN or MLP?
Currently, the biggest bottleneck of KAN is its slow training speed. With the same number of parameters, the training time of KAN is usually 10 times that of MLP. The authors state that, to be honest, they have not made an effort to optimize KAN's efficiency, so they believe that KAN's slow training speed is more of an engineering issue that can be improved in the future rather than a fundamental limitation. If someone wants to train a model quickly, he should use MLP. However, in other cases, KANs should be as good as or better than MLPs, making them worth trying. The decision tree in Figure 6.1 can help decide when to use a KAN. In short, if you care about interpretability and/or accuracy, and slow training is not a major issue, the authors recommend trying KAN.
For more details, please read the original paper.
The above is the detailed content of Transformer wants to become Kansformer? It has taken decades for MLP to usher in challenger KAN. For more information, please follow other related articles on the PHP Chinese website!
 Build your own git server
Build your own git server
 The difference between git and svn
The difference between git and svn
 git undo submitted commit
git undo submitted commit
 How to undo git commit error
How to undo git commit error
 How to compare the file contents of two versions in git
How to compare the file contents of two versions in git
 The difference between static web pages and dynamic web pages
The difference between static web pages and dynamic web pages
 Migrate data from Android phone to Apple phone
Migrate data from Android phone to Apple phone
 location.reload usage
location.reload usage




