Detailed explanation of GQA, the attention mechanism commonly used in large models, and Pytorch code implementation

Grouped Query Attention (Grouped Query Attention) is a multi-query attention method in large language models. Its goal is to achieve the quality of MHA while maintaining the speed of MQA. Grouped Query Attention groups queries so that queries within each group share the same attention weight, which helps reduce computational complexity and increase inference speed.

In this article, we will explain the idea of ​​GQA and how to translate it into code.

GQA is proposed in the paper GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints paper. It is a fairly simple and clean idea, and is built on multi-head attention. above strength.

GQA

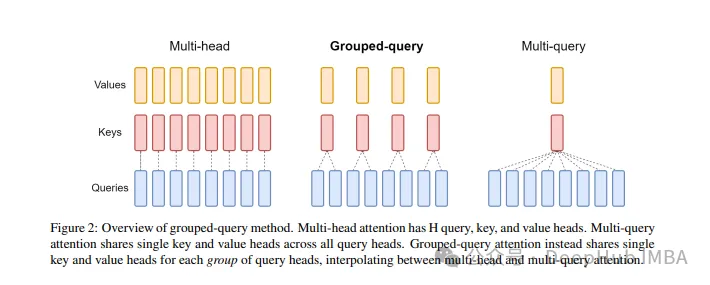
The standard multi-head attention layer (MHA) consists of H query heads, key heads and Value header composition. Each head has D dimensions. The Pytorch code is as follows:

from torch.nn.functional import scaled_dot_product_attention  # shapes: (batch_size, seq_len, num_heads, head_dim) query = torch.randn(1, 256, 8, 64) key = torch.randn(1, 256, 8, 64) value = torch.randn(1, 256, 8, 64)  output = scaled_dot_product_attention(query, key, value) print(output.shape) # torch.Size([1, 256, 8, 64])

For each query header, there is a corresponding key. This process is shown in the figure below:

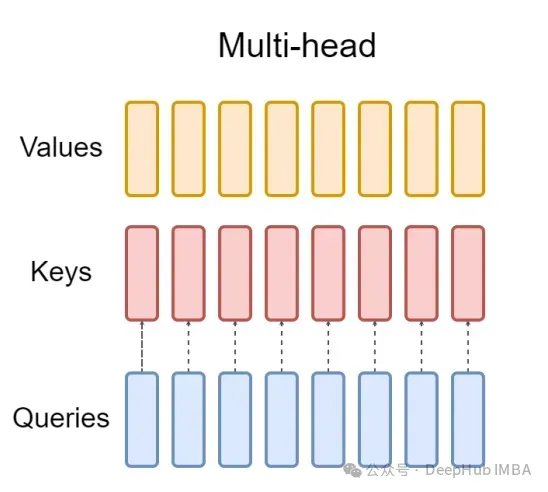
And GQA divides the query header into G groups, and each group shares a key and value. It can be expressed as:

Using visual expression, you can clearly understand the working principle of GQA, just like what we said above. GQA is a fairly simple and clean idea.

Pytorch code implementation

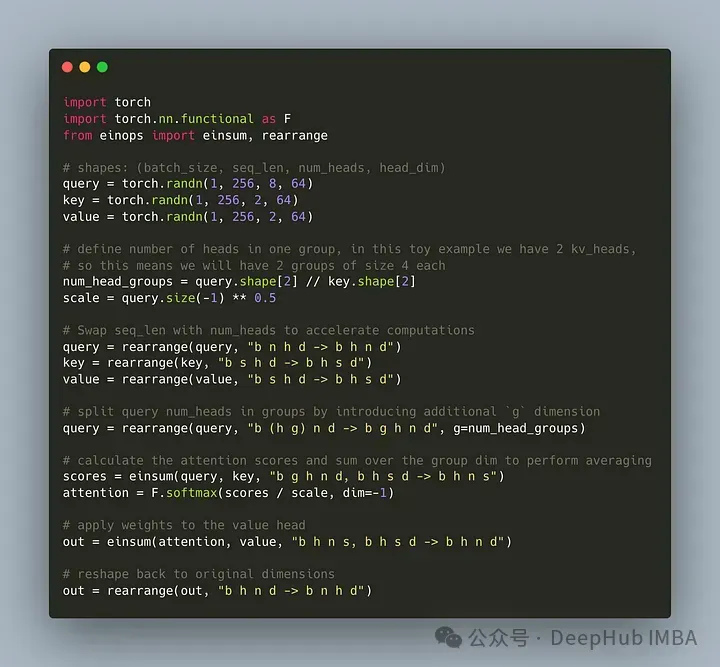
Let us write code to divide the query header into G groups, each group sharing a key and value . We can use the einops library to efficiently perform complex operations on tensors.

First, define the query, keys, and values. Then set the number of attention heads. The number is arbitrary, but it must be ensured that num_heads_for_query % num_heads_for_key = 0, which means it must be divisible. Our definition is as follows:

import torch  # shapes: (batch_size, seq_len, num_heads, head_dim) query = torch.randn(1, 256, 8, 64) key = torch.randn(1, 256, 2, 64) value = torch.randn(1, 256, 2, 64)  num_head_groups = query.shape[2] // key.shape[2] print(num_head_groups) # each group is of size 4 since there are 2 kv_heads

To improve efficiency, swapping the seq_len and num_heads dimensions, einops can be done simply as follows:

from einops import rearrange  query = rearrange(query, "b n h d -> b h n d") key = rearrange(key, "b s h d -> b h s d") value = rearrange(value, "b s h d -> b h s d")

Then the concept of "grouping" needs to be introduced into the query matrix.

from einops import rearrange query = rearrange(query, "b (h g) n d -> b g h n d", g=num_head_groups) print(query.shape) # torch.Size([1, 4, 2, 256, 64])

With the code above we reshape 2D into 2D: for the tensor we defined, the original dimension 8 (the number of heads in the query) is now Split into two groups (to match the number of heads in keys and values), each group size 4.

The last and hardest part is calculating the attention score. But in fact, it can be done in one line through the insum operation. The

from einops import einsum, rearrange # g stands for the number of groups # h stands for the hidden dim # n and s are equal and stands for sequence length scores = einsum(query, key, "b g h n d, b h s d -> b h n s") print(scores.shape) # torch.Size([1, 2, 256, 256])

scores tensor has the same shape as the value tensor above. Let’s see how it works

einsum does two things for us:

1. A query and matrix multiplication of keys . In our case, the shapes of these tensors are (1,4,2,256,64) and (1,2,256,64), so matrix multiplication along the last two dimensions gives us (1,4,2,256,256).

2. Sum the elements in the second dimension (dimension g) - if the dimension is omitted in the specified output shape, einsum will automatically complete this work, so The summation is used to match the number of keys and values ​​in the header.

Finally, note the standard multiplication of fractions and values:

import torch.nn.functional as F  scale = query.size(-1) ** 0.5 attention = F.softmax(similarity / scale, dim=-1)  # here we do just a standard matrix multiplication out = einsum(attention, value, "b h n s, b h s d -> b h n d")  # finally, just reshape back to the (batch_size, seq_len, num_kv_heads, hidden_dim) out = rearrange(out, "b h n d -> b n h d") print(out.shape) # torch.Size([1, 256, 2, 64])

The simplest GQA implementation is now complete, requiring less than 16 lines of python code:

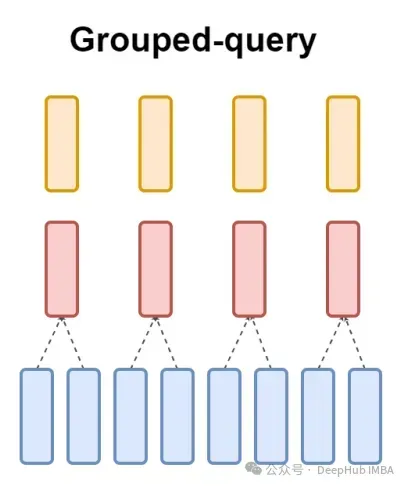
Finally, I will briefly mention A word about MQA: Multiple Query Attention (MQA) is another popular method to simplify MHA. All queries will share the same keys and values. The schematic diagram is as follows:

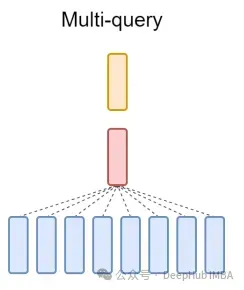
As you can see, both MQA and MHA can be derived from GQA. GQA with a single key and value is equivalent to MQA, while GQA with groups equal to the number of headers is equivalent to MHA.

What are the benefits of GQA?

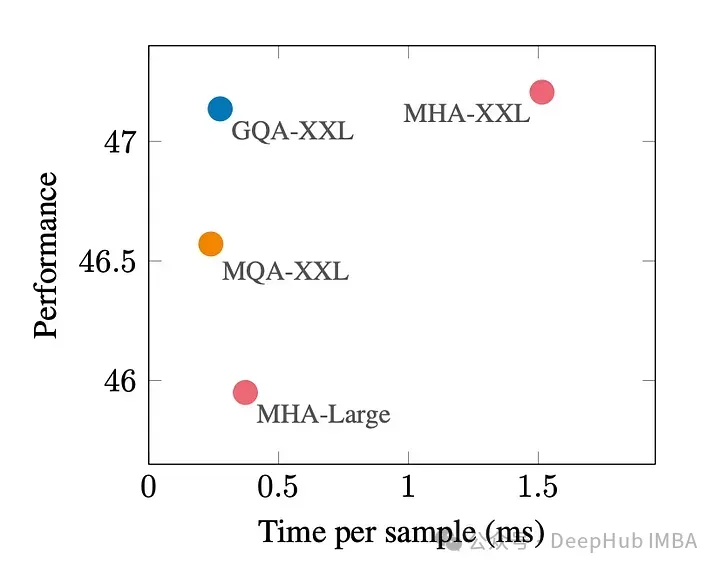
GQA is one between the best performance (MQA) and the best model quality (MHA) Very good trade-off.

The following figure shows that using GQA, you can obtain almost the same model quality as MHA, while increasing the processing time by 3 times, reaching the performance of MQA. This may be essential for high load systems.

There is no official implementation of GQA in pytorch. So I found a better unofficial implementation. If you are interested, you can try it:

//m.sbmmt.com/link/5b52e27a9d5bf294f5b593c4c071500e

GQA paper:

//m.sbmmt.com/link/e4ba31fba036a999321d5460f7f2d1d1