
Newton iteration method:
function[x0,n]=newton(fx,dfx,x0,tol,N)
% Newton iteration method
% The first parameter fx is the desired function expression about variable x.
% The second parameter dfx is the first derivative of fx.
% x0 is the initial value of iteration.
% tol is the iteration error limit.
% N Maximum number of iterations.
x=x0;f0=eval(fx);df0=eval(dfx);
n=0;
disp('[ n xn xn 1 delta ]');
while n
x1=x0-f0/df0;
x=x1;f1=eval(fx);df1=eval(dfx);
delta=abs(x0-x1);
% X=[n,x0,x1,delta];
disp(X); % is used to display intermediate results
if delta
fprintf('Iterative calculation successful')
return
else
n=n 1;
x0=x1;f0=f1;df0=df1;
end
end
if n==N 1
fprintf('Iteration calculation failed')
end
The other two can be modified slightly on this basis.
Give you a complete version:
% Newton’s method for solving nonlinear equations
function main()
clc; clear all;
f = @(x)log(x sin(x)); % test function
df = @(x)(1 cos(x))/(x sin(x)); % derivative function
x0 = 0.1; % iteration initial value
x = TestNewton(f, df, x0) % Newton’s method solution
function x = TestNewton(fname, dfname, x0, e, N)
% Purpose: Newton iteration method to solve nonlinear equation f(x)=0
% fname and dfname respectively represent the M function handle or embedded function expression of f(x) and its derivative function
% x0 is the iteration initial value, e is the accuracy (default value 1e-7)
% x returns a numerical solution and displays the calculation process. Set the upper limit of the number of iterations N to prevent divergence (default 500 times)
% Input parameters
if nargin
N = 500;
end
if nargin
e = 1e-7;
end
x = x0; % initial value
x0 = x 2*e; % float
k = 0; % number of steps
fprintf('x[%d]= .9f\n', k, x) % print information
while abs(x0-x)>e & k
k = k 1; % record the number of steps
x0 = x; % update x(k)
x = x0 - feval(fname,x0)/feval(dfname,x0); % update x(k 1)
fprintf('x[%d]= .9f\n', k, x) % print information
end
if k == N
fprintf('The maximum number of iterations has been reached'); % End of iteration
end
result:
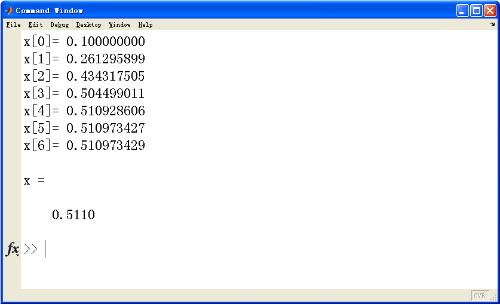
The above is the detailed content of Detailed explanation of the implementation method of iterative method of nonlinear equations in matlab. For more information, please follow other related articles on the PHP Chinese website!




