
Complex mathematical reasoning is an important indicator for evaluating the reasoning ability of large language models. Currently, the commonly used mathematical reasoning data sets have limited sample sizes and insufficient problem diversity, resulting in the phenomenon of "reversal curse" in large language models, that is, a A language model trained on "A is B" cannot be generalized to "B is A" [1]. The specific form of this phenomenon in mathematical reasoning tasks is: given a mathematical problem, the language model is good at using forward reasoning to solve the problem but lacks the ability to solve the problem with reverse reasoning. Reverse reasoning is very common in mathematical problems, as shown in the following 2 examples.
In order to improve the forward sum of the model For reverse reasoning capabilities, researchers from Cambridge, Hong Kong University of Science and Technology, and Huawei proposed the MetaMathQA data set based on two commonly used mathematical data sets (GSM8K and MATH): a mathematical reasoning data set with wide coverage and high quality. MetaMathQA consists of 395K forward-inverse mathematical question-answer pairs generated by a large language model. They fine-tuned LLaMA-2 on the MetaMathQA data set to obtain MetaMath, a large language model focusing on mathematical reasoning (forward and inverse), which reached SOTA on the mathematical reasoning data set. The MetaMathQA dataset and MetaMath models at different scales have been open sourced for use by researchers.

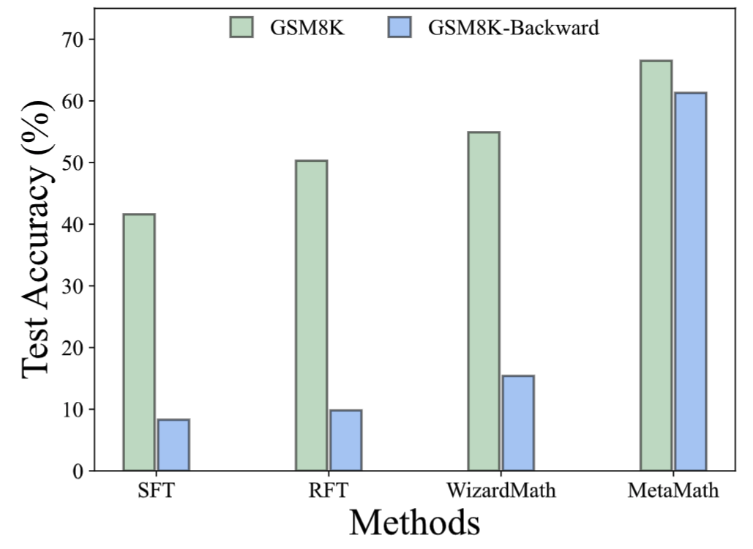
In the GSM8K-Backward data set, we constructed a reverse inference experiment. Experimental results show that compared with methods such as SFT, RFT, and WizardMath, the current method performs poorly on inverse inference problems. In contrast, MetaMath models achieve excellent performance in both forward and backward inference
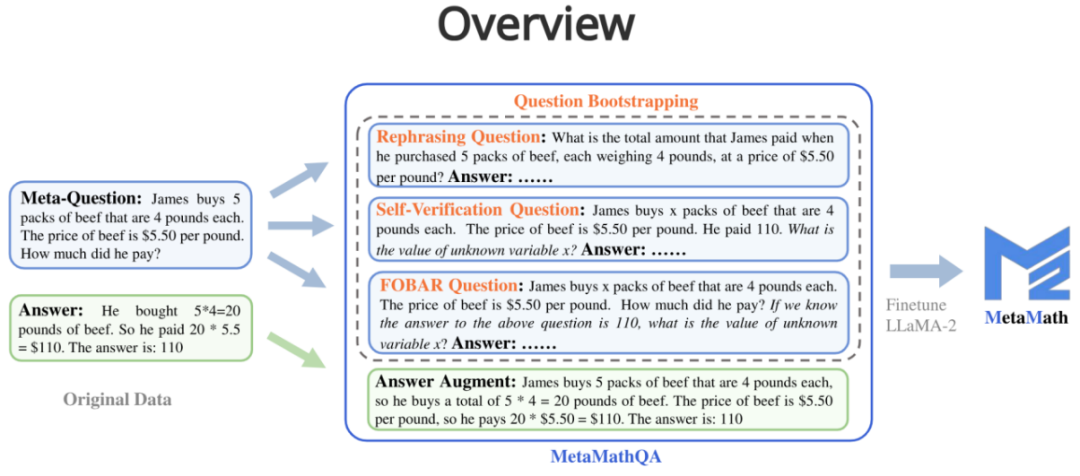
MetaMathQA contains four data augmentation methods:
1. Answer Augmentation (answer Enhancement): Given a problem, a thinking chain that can get the correct result is generated through a large language model as data augmentation.
2. Rephrasing Question (question rewriting enhancement): Given meta-question , rewrite the problem through a large language model and generate a thought chain that gets the correct result as data augmentation.
##3. FOBAR Question (FOBAR reverse question enhancement):Given the meta-question, the number in the mask condition is Example: "If we know the answer to the above question is 110, what is the value of unknown variable x?").
4. Self-Verification Question (Self-Verification reverse question enhancement): Based on FOBAR, data augmentation is performed by rewriting the inverse problem part into statements using a large language model (rewritten example: "How much did he pay?" (with the answer 110) was rewritten into "He paid 110").

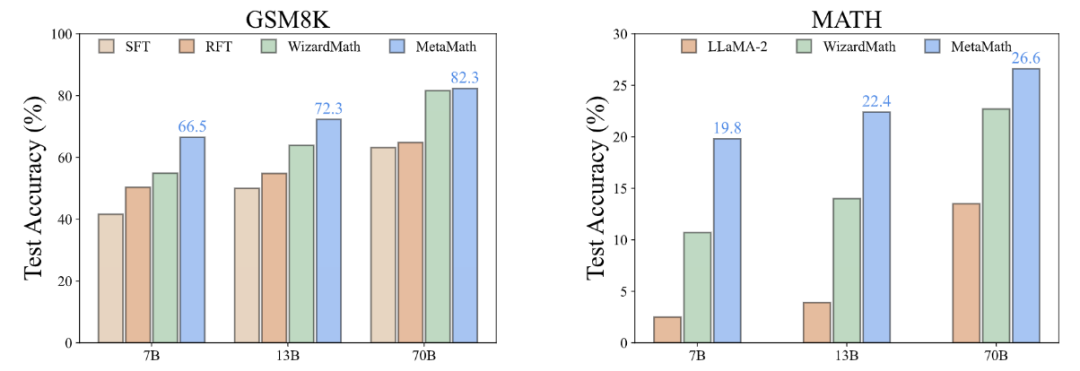
According to the "Surface Alignment Assumption" [2], The power of large language models comes from pre-training, and data from downstream tasks activates the inherent capabilities of the language model learned during pre-training. Therefore, this raises two important questions: (i) which type of data activates latent knowledge most effectively, and (ii) why is one dataset better at such activation than another?
Why is MetaMathQA useful? Improved the quality of thought chain data (Perplexity)
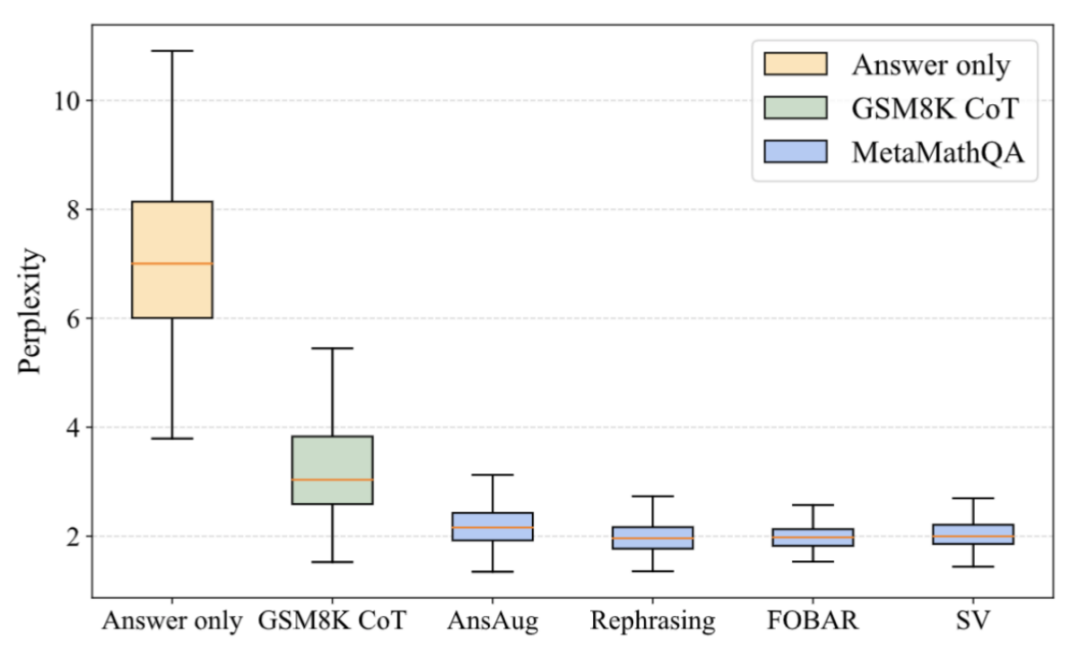 ##As shown in the figure above, the researchers calculated Perplexity of the LLaMA-2-7B model on answer-only data, GSM8K CoT, and various parts of the MetaMathQA dataset. The perplexity of the MetaMathQA dataset is significantly lower than the other two datasets, indicating that it has higher learnability and may be more helpful in revealing the latent knowledge of the model
##As shown in the figure above, the researchers calculated Perplexity of the LLaMA-2-7B model on answer-only data, GSM8K CoT, and various parts of the MetaMathQA dataset. The perplexity of the MetaMathQA dataset is significantly lower than the other two datasets, indicating that it has higher learnability and may be more helpful in revealing the latent knowledge of the model
Why is MetaMathQA useful? Increased the diversity of thought chain data (Diversity)
By comparing the diversity gain of the data and the accuracy gain of the model, the researchers found that the introduction of the same amount of augmented data by reformulation, FOBAR and SV all brought A significant diversity gain was achieved and the accuracy of the model was significantly improved. In contrast, using answer augmentation alone resulted in significant saturation of accuracy. After the accuracy reaches saturation, adding AnsAug data will only bring limited performance improvement
The above is the detailed content of Reverse thinking: MetaMath new mathematical reasoning language model trains large models. For more information, please follow other related articles on the PHP Chinese website!




