
Java Collection Framework Java Collection Framework, also known as container container, is the definition A set of interfaces and their implementation classes under the java.util package.
Its main performance is to place multiple elements in a unit, which is used to quickly and conveniently store, retrieve, and manage these elements, which is commonly known as CRUD.
Overview of classes and interfaces:
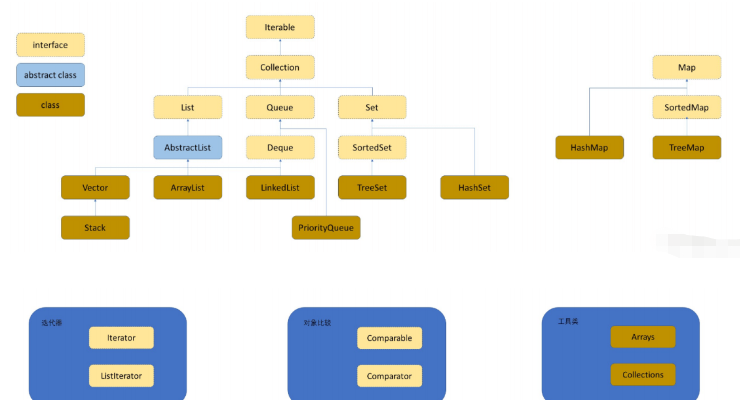
Collection: is an interface that contains most commonly used containers Some methods
List: is an interface that standardizes the methods to be implemented in ArrayList and LinkedList
ArrayList: implements the List interface, and the bottom layer is a dynamic type sequence list
LinkedList: implements the List interface, the bottom layer is a doubly linked list
Stack: the bottom layer is a stack, and the stack is a special sequence list
Queue: The bottom layer is a queue, which is a special sequence table.
Deque: It is an interface.
Set: Set is an interface, and the K model is placed in it.
HashSet: The bottom layer is a hash bucket, and the query time complexity is O(1)
TreeSet: The bottom layer is a red-black tree, The time complexity of the query is O(), about the key-ordered
Map: mapping, which stores the key-value pairs of the K-V model
HashMap: The bottom layer is a hash bucket, and the query time complexity is O(1)
TreeMap: The bottom layer is a red-black tree, and the query time complexity is O(), About key order
Algorithm (Algorithm): It is a well-defined calculation process. It takes one or one Groups of values are input and produce a value or group of values as output. An algorithm is a series of computational steps designed to transform input data into output results.
Algorithm efficiency analysis is divided into two types: the first is time efficiency, and the second is space efficiency. Time efficiency is called time complexity, while space efficiency is called space complexity. Time complexity mainly measures the running speed of an algorithm, while space complexity mainly measures the extra space required by an algorithm. In the early days of computer development, the storage capacity of computers was very small. So we care a lot about space complexity. With the rapid development of the computer industry, the storage capacity of computers has reached a very high level. So we no longer need to pay special attention to the space complexity of an algorithm.
Time complexity is a mathematical function in computer science that represents the running time of an algorithm and quantitatively describes the algorithm time efficiency. The execution time of an algorithm cannot be calculated theoretically. The time consuming can only be known after the program is actually run on the computer. Although each algorithm can be tested on a computer, this is very cumbersome, so there is a way to analyze it through time complexity. The time complexity of an algorithm is proportional to the time it takes to execute the number of statements, and the time complexity depends on the number of executions of the basic operations in the algorithm.
// 请计算一下func1基本操作执行了多少次?
void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++) {
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}The number of basic operations performed by Func1: F(N)=N^2 2*N 10
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
In fact, when we calculate the time complexity, we do not actually have to calculate the exact number of executions, but only the approximate number of executions, so here we use the asymptotic of Big O Notation.
Big O notation (Big O notation): It is a mathematical symbol used to describe the asymptotic behavior of a function
Use The constant 1 replaces all additive constants in run time.
In the modified number of runs function, only the highest order term is retained.
If the highest-order term exists and is not 1, remove the constant multiplied by this term. The result is Big O order.
After using the asymptotic representation of big O, the time complexity of Func1 is: O(n^2)
N = 10 F (N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
Through the above content, we can see that the Big O asymptotic notation excludes items that have little impact on the result, thus expressing the number of executions concisely and clearly. In addition, the time complexity of some algorithms has best, average and worst cases:
Worst case: the maximum number of runs (upper bound) for any input scale
Average case: any input scale The expected number of runs
Best case: the minimum number of runs (lower bound) for any input size
For example: searching for a data x
in an array of length N Scenario:
found 1 time Worst case:
found N times平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
对于一个算法而言,空间复杂度表示它在执行期间所需的临时存储空间大小。空间复杂度的计算方式并非程序所占用的字节数量,因为这并没有太大的意义;实际上,空间复杂度的计算基于变量的数量。大O渐进表示法通常用来计算空间复杂度,其计算规则类似于实践复杂度的计算规则。
实例1:
// 计算bubbleSort的空间复杂度?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if(sorted == true) {
break;
}
}
}实例2:
// 计算fibonacci的空间复杂度?
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}实例3:
// 计算阶乘递归Factorial的空间复杂度?
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}实例1使用了常数个额外空间,所以空间复杂度为 O(1)
实例2动态开辟了N个空间,空间复杂度为 O(N)
实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
The above is the detailed content of What are the collection framework and common algorithms of Java data structure?. For more information, please follow other related articles on the PHP Chinese website!




