
For example, we have two sentences:
ls = ['我永远喜欢三上悠亚', '三上悠亚又出新作了']
Under jieba word segmentation, we can get the following effect:
We can construct a co-occurrence matrix based on keywords:
['', '我', '永远', '喜欢', '三上', '悠亚', '又', '出', '新作', '了'] ['我', 0, 1, 1, 1, 1, 0, 0, 0, 0] ['永远', 1, 0, 1, 1, 1, 0, 0, 0, 0] ['喜欢' 1, 1, 0, 1, 1, 0, 0, 0, 0] ['三上', 1, 1, 1, 0, 1, 1, 1, 1, 1] ['悠亚', 1, 1, 1, 1, 0, 1, 1, 1, 1] ['又', 0, 0, 0, 1, 1, 0, 1, 1, 1] ['出', 0, 0, 0, 1, 1, 1, 0, 1, 1] ['新作', 0, 0, 0, 1, 1, 1, 1, 0, 1] ['了', 0, 0, 0, 1, 1, 1, 1, 1, 0]]
Explain, "I will always like Mikami Yua", in this sentence, "I" and "forever" appear together Once, 1 on [i][j] and [j][i] corresponding to the co-occurrence matrix, and so on.
Based on this reason, we can find that the characteristics of the co-occurrence matrix are:
[0][0] of the co-occurrence matrix is null.
The first row and first column of the co-occurrence matrix are keywords.
The diagonal is all 0.
The co-occurrence matrix is actually a symmetric matrix.
Of course, in actual operation, these keywords need to be cleaned so that such visualization can be clean.
The two-dimensional array data_array of keywords for each article.
The set_word of all keywords.
Create a matrix matrix with keyword length 1.
The first row and first column of the assignment matrix are keywords.
Set the matrix diagonal to 0.
Traverse the formatted_data, and combine the extracted row keywords and extracted column keywords, and the co-occurrence rate is 1.
# coding:utf-8
import numpy as np
import pandas as pd
import jieba.analyse
import os
# 获取关键词
def Get_file_keywords(dir):
data_array = [] # 每篇文章关键词的二维数组
set_word = [] # 所有关键词的集合
try:
fo = open('dic_test.txt', 'w+', encoding='UTF-8')
# keywords = fo.read()
for home, dirs, files in os.walk(dir): # 遍历文件夹下的每篇文章
for filename in files:
fullname = os.path.join(home, filename)
f = open(fullname, 'r', encoding='UTF-8')
sentence = f.read()
words = " ".join(jieba.analyse.extract_tags(sentence=sentence, topK=30, withWeight=False,
allowPOS=('n'))) # TF-IDF分词
words = words.split(' ')
data_array.append(words)
for word in words:
if word not in set_word:
set_word.append(word)
set_word = list(set(set_word)) # 所有关键词的集合
return data_array, set_word
except Exception as reason:
print('出现错误:', reason)
return data_array, set_word
# 初始化矩阵
def build_matirx(set_word):
edge = len(set_word) + 1 # 建立矩阵,矩阵的高度和宽度为关键词集合的长度+1
'''matrix = np.zeros((edge, edge), dtype=str)''' # 另一种初始化方法
matrix = [['' for j in range(edge)] for i in range(edge)] # 初始化矩阵
matrix[0][1:] = np.array(set_word)
matrix = list(map(list, zip(*matrix)))
matrix[0][1:] = np.array(set_word) # 赋值矩阵的第一行与第一列
return matrix
# 计算各个关键词的共现次数
def count_matrix(matrix, formated_data):
for row in range(1, len(matrix)):
# 遍历矩阵第一行,跳过下标为0的元素
for col in range(1, len(matrix)):
# 遍历矩阵第一列,跳过下标为0的元素
# 实际上就是为了跳过matrix中下标为[0][0]的元素,因为[0][0]为空,不为关键词
if matrix[0][row] == matrix[col][0]:
# 如果取出的行关键词和取出的列关键词相同,则其对应的共现次数为0,即矩阵对角线为0
matrix[col][row] = str(0)
else:
counter = 0 # 初始化计数器
for ech in formated_data:
# 遍历格式化后的原始数据,让取出的行关键词和取出的列关键词进行组合,
# 再放到每条原始数据中查询
if matrix[0][row] in ech and matrix[col][0] in ech:
counter += 1
else:
continue
matrix[col][row] = str(counter)
return matrix
def main():
formated_data, set_word = Get_file_keywords(r'D:\untitled\test')
print(set_word)
print(formated_data)
matrix = build_matirx(set_word)
matrix = count_matrix(matrix, formated_data)
data1 = pd.DataFrame(matrix)
data1.to_csv('data.csv', index=0, columns=None, encoding='utf_8_sig')
main()Count the number of times two phrases appear together in the text to describe the intimacy between the phrases
code (The diagonal element I am looking for here is the number of times the field appears in the text. Total times):
import pandas as pd
def gx_matrix(vol_li):
# 整合一下,输入是df列,输出直接是矩阵
names = locals()
all_col0 = [] # 用来后续求所有字段的集合
for row in vol_li:
all_col0 += row
for each in row: # 对每行的元素进行处理,存在该字段字典的话,再进行后续判断,否则创造该字段字典
try:
for each2 in row: # 对已存在字典,循环该行每个元素,存在则在已有次数上加一,第一次出现创建键值对“字段:1”
try:
names['dic_' + each][each2] = names['dic_' + each][each2] + 1 # 尝试,一起出现过的话,直接加1
except:
names['dic_' + each][each2] = 1 # 没有的话,第一次加1
except:
names['dic_' + each] = dict.fromkeys(row, 1) # 字段首次出现,创造字典
# 根据生成的计数字典生成矩阵
all_col = list(set(all_col0)) # 所有的字段(所有动物的集合)
all_col.sort(reverse=False) # 给定词汇列表排序排序,为了和生成空矩阵的横向列名一致
df_final0 = pd.DataFrame(columns=all_col) # 生成空矩阵
for each in all_col: # 空矩阵中每列,存在给字段字典,转为一列存入矩阵,否则先创造全为零的字典,再填充进矩阵
try:
temp = pd.DataFrame(names['dic_' + each], index=[each])
except:
names['dic_' + each] = dict.fromkeys(all_col, 0)
temp = pd.DataFrame(names['dic_' + each], index=[each])
df_final0 = pd.concat([df_final0, temp]) # 拼接
df_final = df_final0.fillna(0)
return df_final
if __name__ == '__main__':
temp1 = ['狗', '狮子', '孔雀', '猪']
temp2 = ['大象', '狮子', '老虎', '猪']
temp3 = ['大象', '北极熊', '老虎', '猪']
temp4 = ['大象', '狗', '老虎', '小鸡']
temp5 = ['狐狸', '狮子', '老虎', '猪']
temp_all = [temp2, temp1, temp3, temp4, temp5]
vol_li = pd.Series(temp_all)
df_matrix = gx_matrix(vol_li)
print(df_matrix)The input is a series that looks like this

Find the dictionary for each field and the number of occurrences of each field

Finally converted to df
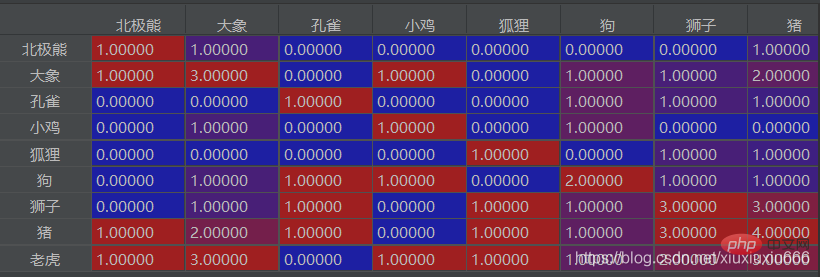
If you use the column of the elephant here, divide by the large The number of times the elephant appears, the higher the ratio, indicates that the two appear together more times. If in this series of ratios, the ratio of two elements a and b is greater than 0.8 (not necessarily 0.8), it means that they are both relatively high. It means that a and b appear together with the elephant three times a lot! ! !
You can find the word combinations that often appear together in the text. For example, in the second column here, the elephant appears 3 times in total, with the tiger 3 times, and with the pig 2 times, you can deduce that the big Elephants, tigers, and pigs have a higher probability of appearing together.
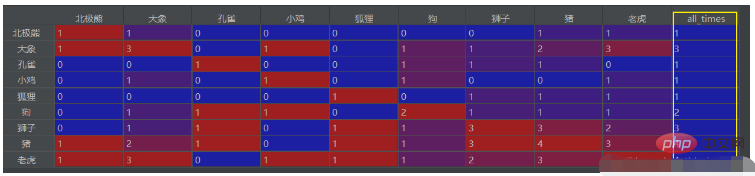
You can also extract the total number of occurrences and put them in the last column, then the code is:
# 计算每个字段的出现次数,并列为最后一行
df_final['all_times'] = ''
for each in df_final0.columns:
df_final['all_times'].loc[each] = df_final0.loc[each, each]Put it after the above code df_final = df_final0.fillna(0)
The result is
The above is the detailed content of How to implement co-occurrence matrix in python. For more information, please follow other related articles on the PHP Chinese website!




