Quantum machine learning beyond kernel methods, a unified framework for quantum learning models

Machine learning algorithms based on parameterized quantum circuits are prime candidates for near-term applications on noisy quantum computers. In this direction, various types of quantum machine learning models have been introduced and extensively studied. However, our understanding of how these models compare to each other and to classical models remains limited.

Recently, a research team from the University of Innsbruck, Austria, identified a constructive framework that captures all standard models based on parameterized quantum circuits: the linear quantum model.

The researchers show how using tools from quantum information theory to efficiently map data re-upload circuits into a simpler picture of a linear model in quantum Hilbert space. Furthermore, the experimentally relevant resource requirements of these models are analyzed in terms of the number of qubits and the amount of data that needs to be learned. Recent results based on classical machine learning demonstrate that linear quantum models must use many more qubits than data reupload models to solve certain learning tasks, while kernel methods also require many more data points. The results provide a more comprehensive understanding of quantum machine learning models, as well as insights into the compatibility of different models with NISQ constraints.

The research is titled "Quantum machine learning beyond kernel methods" and was published in "Nature Communications on January 31, 2023 "superior.

##Paper link: https: //www.nature.com/articles/s41467-023-36159-y​

In the current noisy intermediate-level quantum (NISQ) era, it has been proposed Some ways to build useful quantum algorithms compatible with slight hardware constraints. Most of these methods involve the specification of Ansatz quantum circuits, optimized in a classical manner to solve specific computational tasks. In addition to variational quantum signature solvers and variants of quantum approximate optimization algorithms in chemistry, machine learning methods based on such parameterized quantum circuits are one of the most promising practical applications for generating quantum advantages.

Kernel methods are a type of pattern recognition algorithm. Its purpose is to find and learn the mutual relationships in a set of data. The kernel method is an effective way to solve nonlinear pattern analysis problems. Its core idea is: first, embed the original data into a suitable high-dimensional feature space through some nonlinear mapping; then, use a general linear learner to New modes of analysis and processing in space.

Previous work has made great progress in this direction by exploiting the connection between some quantum models and kernel methods of classical machine learning. Many quantum models indeed operate by encoding data in a high-dimensional Hilbert space and modeling properties of the data using only inner products evaluated in this feature space. This is also how the nuclear method works.

Based on this similarity, a given quantum encoding can be used to define two types of models: (a) Explicit quantum models, in which the data points are encoded according to a variable that specifies their label Measurements are made on separate observables; or (b) implicit kernel models, where a weighted inner product of encoded data points is used to assign labels. In the quantum machine learning literature, a lot of emphasis is placed on implicit models.

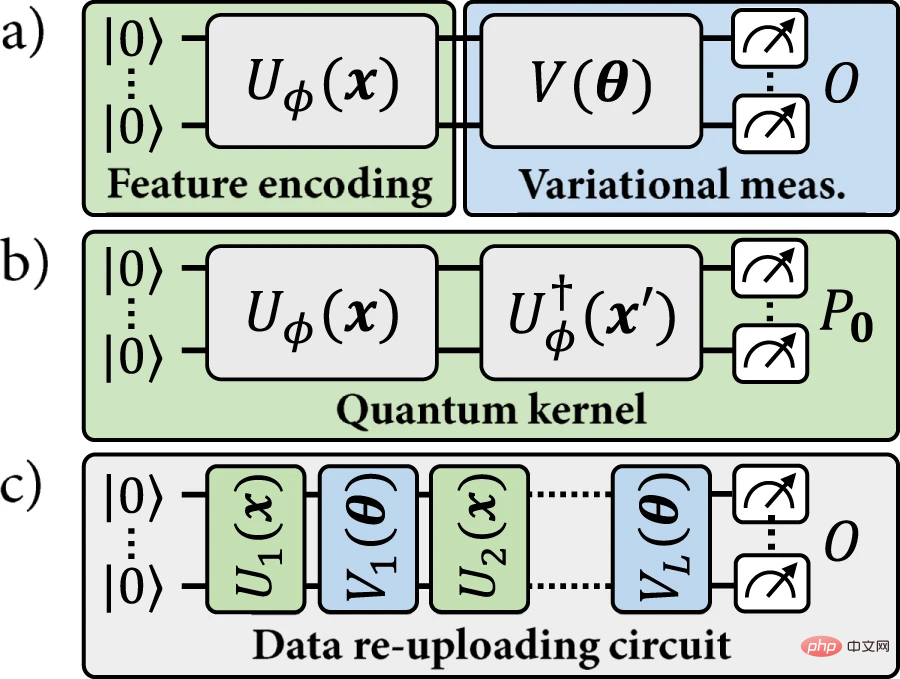
Figure 1: The quantum machine learning model studied in this work. (Source: paper)

#Recently, there has been progress in the so-called data re-uploading model. The data re-upload model can be seen as a generalization of the explicit model. However, this generalization also breaks the correspondence with the implicit model, since a given data point x no longer corresponds to a fixed encoding point ρ(x). Data reupload models are strictly more general than explicit models, and they are not compatible with the kernel model paradigm. So far, it remains an open question whether some advantages can be obtained from data re-upload models with the guarantee of kernel methods.

In this work, the researchers introduce a unified framework for explicit, implicit and data re-upload quantum models.

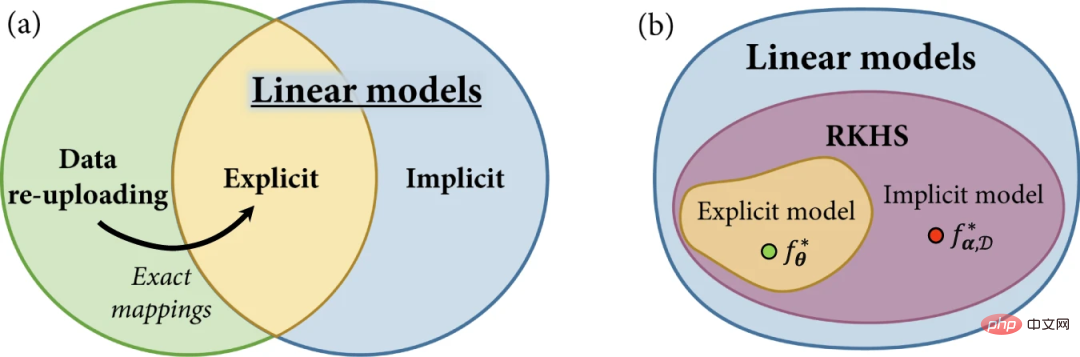
Figure 2: Model family in quantum machine learning. (Source: Paper)

Unified Framework for Quantum Learning Models

First review the concept of linear quantum models and define linear models in terms of quantum feature space Explain explicit and implicit models. Then, data reupload models are presented and shown that although defined as generalizations of explicit models, they can also be implemented by linear models in larger Hilbert spaces.

Linear Quantum Model

The figure below gives an illustrative structure to visually illustrate how to implement the mapping from data re-upload to an explicit model.

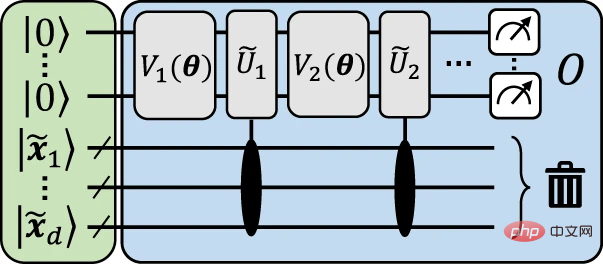
Figure 3: Illustrative explicit model approximating the data reupload circuit. (Source: paper)

#The general idea behind this structure is to encode the input data x into auxiliary qubits to finite accuracy, which can then be reused using Data-independent unitaries are used to approximate data encoding gates.

Now moving on to the main structure, resulting in data re-uploading and exact mapping between explicit models. Here, relying on a similar idea to the previous structure, the input data is encoded on the auxiliary qubit, and then the encoding gate is implemented on the working qubit using data-independent operations. The difference here is to use gate-teleportation, a type of measurement-based quantum computing, to implement encoding gates directly on the auxiliary qubits and teleport them back (via entanglement measurements) to the working qubits when needed superior.

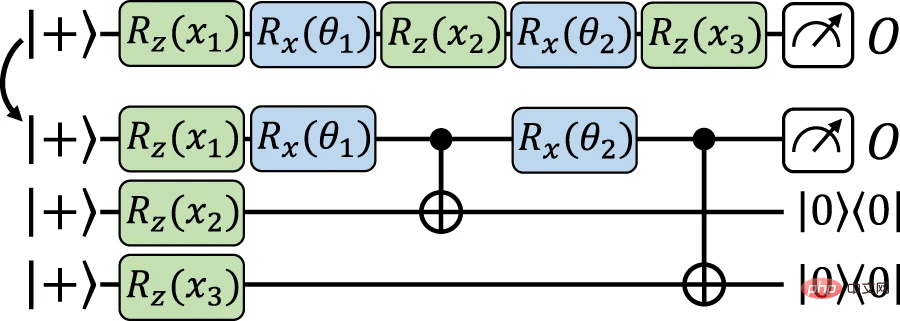
Figure 4: Using gated teleportation to reupload the model from data to an equivalent explicit model Precise mapping. (Source: paper)

#The researchers demonstrated that linear quantum models can describe not only explicit and implicit models, but also data re-upload circuits. More specifically, any hypothesis class of data reupload models can be mapped to an equivalent class of explicit models, i.e., linear models with a restricted family of observables.

The researchers then more rigorously analyzed the advantages of explicit and data re-upload models over implicit models. In the example, the efficiency of the quantum model in solving the learning task is quantified by the number of qubits and the training set size required to achieve a non-trivial expected loss. The learning task of interest is learning odd and even functions.

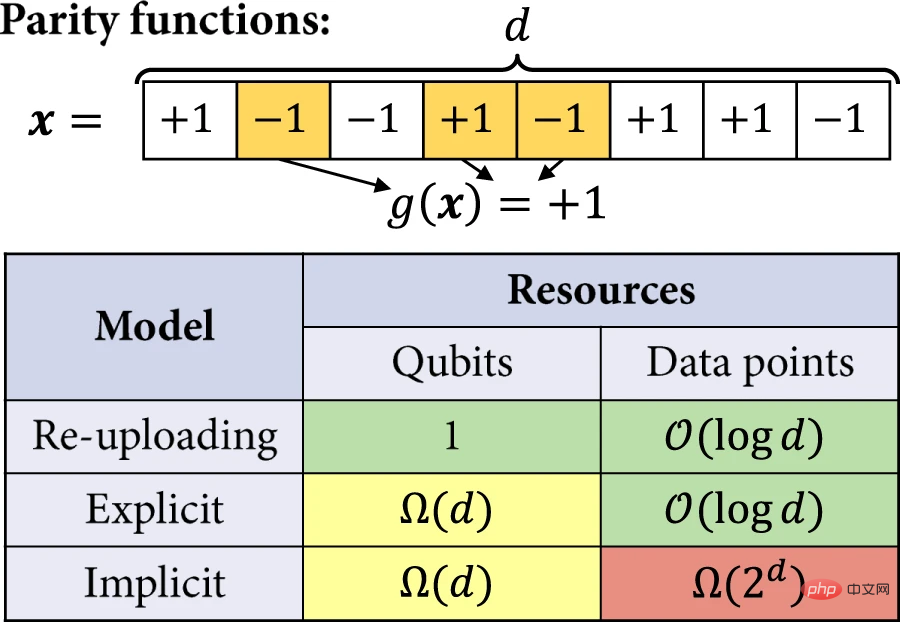
Figure 5: Learning to separate. (Source: Paper)

Quantum advantage beyond nuclear methods

A major challenge in quantum machine learning is to show that the quantum methods discussed in this work Learning advantages over (standard) classical methods can be achieved.

In this research, Huang et al. of Google Quantum Artificial Intelligence (​ //m.sbmmt.com/link/4dfd2a142d36707f8043c40ce0746761​​) It is recommended to study the target function itself by ( Explicit) learning tasks for quantum model generation.

Similar to Huang et al., the researchers performed the regression task using input data from the fashion-MNIST dataset, where each example was a 28x28 grayscale image.

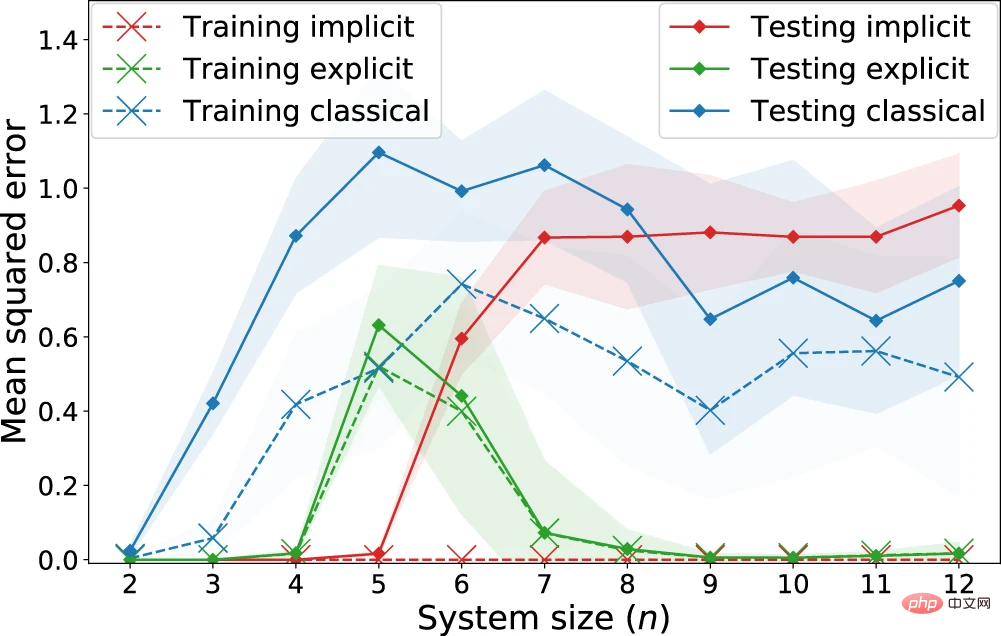
Figure 6: Performance of explicit, implicit and classical models on the "quantum customization" learning task Return to performance. (Source: Paper)

#Observation: Implicit models systematically achieve lower training losses than explicit models. Especially for non-regularized losses, the implicit model achieves a training loss of 0. On the other hand, regarding the test losses that represent the expected losses, there is a clear separation starting from n = 7 qubits, where the classical model starts to have competitive performance with the implicit model, while the explicit model clearly outperforms both of them. This suggests that the presence of quantum advantage should not be assessed solely by comparing classical models with quantum kernel methods, as explicit (or data re-uploading) models can also hide better learning performance.

These results give us a more comprehensive understanding of the field of quantum machine learning and broaden our view on the types of models to achieve practical learning advantages in NISQ mechanisms.

The researchers believe that the learning task of demonstrating the existence of exponential learning separation between different quantum models is based on odd and even functions, which is not a conceptual class of practical interest in machine learning. However, the lower bound results can also be extended to other learning tasks with large-dimensional concept classes (i.e., consisting of many orthogonal functions).

Quantum kernel methods necessarily require many data points that scale linearly with this dimension, and as we show in our results, the flexibility of the data re-upload circuit and the explicit model Limited expression capabilities to save a lot of resources. Exploring how and when these models can be tailored to the machine learning task at hand remains an interesting research direction.

The above is the detailed content of Quantum machine learning beyond kernel methods, a unified framework for quantum learning models. For more information, please follow other related articles on the PHP Chinese website!