New research from Google and DeepMind: How does inductive bias affect model scaling?

Scaling of Transformer models has aroused the research interest of many scholars in recent years. However, not much is known about the scaling properties of different inductive biases imposed by model architectures. It is often assumed that improvements at a specific scale (computation, size, etc.) can be transferred to different scales and computational regions.

However, it is crucial to understand the interaction between architecture and scaling laws, and it is of great research significance to design models that perform well at different scales. Several questions remain to be clarified: Do model architectures scale differently? If so, how does inductive bias affect scaling performance? How does it affect upstream (pre-training) and downstream (transfer) tasks?

In a recent paper, researchers at Google sought to understand the impact of inductive bias (architecture) on language model scaling . To do this, the researchers pretrained and fine-tuned ten different model architectures across multiple computational regions and scales (from 15 million to 40 billion parameters). Overall, they pretrained and fine-tuned more than 100 models of different architectures and sizes and presented insights and challenges in scaling these ten different architectures.

They also note that scaling these models is not as simple as it seems, that is, the complex details of scaling are intertwined with the architectural choices studied in detail in this article. For example, a feature of Universal Transformers (and ALBERT) is parameter sharing. This architectural choice significantly warps the scaling behavior compared to the standard Transformer not only in terms of performance, but also in terms of computational metrics such as FLOPs, speed, and number of parameters. In contrast, models like Switch Transformers are quite different, with an unusual relationship between FLOPs and parameter quantities.

Specifically, the main contributions of this article are as follows:

• The first derivation of different inductive biases and the scaling law of the model architecture. The researchers found that this scaling factor varied significantly across models and noted that this is an important consideration in model development. It turns out that of all ten architectures they considered, the vanilla Transformer had the best scaling performance, even if it wasn't the best in absolute terms per compute area. Researchers have observed that
• A model that works well in one computational scaling region is not necessarily the best model in another computational scaling region. Additionally, they found that some models, while performing well in low-computation regions, were difficult to scale. This means that it is difficult to get a complete picture of the model's scalability by comparing point by point in a certain computational area. Researchers found that
• when it comes to scaling different model architectures, upstream pre-training perplexity may be less relevant to downstream transfer. Therefore, the underlying architecture and inductive bias are also critical for downstream migration. The researchers highlighted the difficulty of scaling under certain architectures and showed that some models did not scale (or scaled with a negative trend). They also found a tendency for linear temporal attention models (such as Performer) to be difficult to scale.
• Methods and Experiments

In the third chapter of the paper, the researcher outlines the overall experimental setup and introduces the model evaluated in the experiment.

Table 1 below shows the main results of this article, including the number of trainable parameters, FLOPs (single forward pass) and speed (steps per second). In addition, it also includes Validate perplexity (upstream pre-training) and results on 17 downstream tasks.

Are all models scaled the same way?

Figure 2 below shows the scaling behavior of all models when increasing the number of FLOPs. It can be observed that the scaling behavior of all models is quite unique and different, i.e. most of them are different from the standard Transformer. Perhaps the biggest finding here is that most models (e.g., LConv, Evolution) appear to perform on par or better than the standard Transformer, but fail to scale with higher compute budgets.

Another interesting trend is that "linear" Transformers, such as Performer, do not scale. As shown in Figure 2i, compared from base to large scale, the pre-training perplexity only dropped by 2.7%. For the vanilla Transformer this figure is 8.4%.

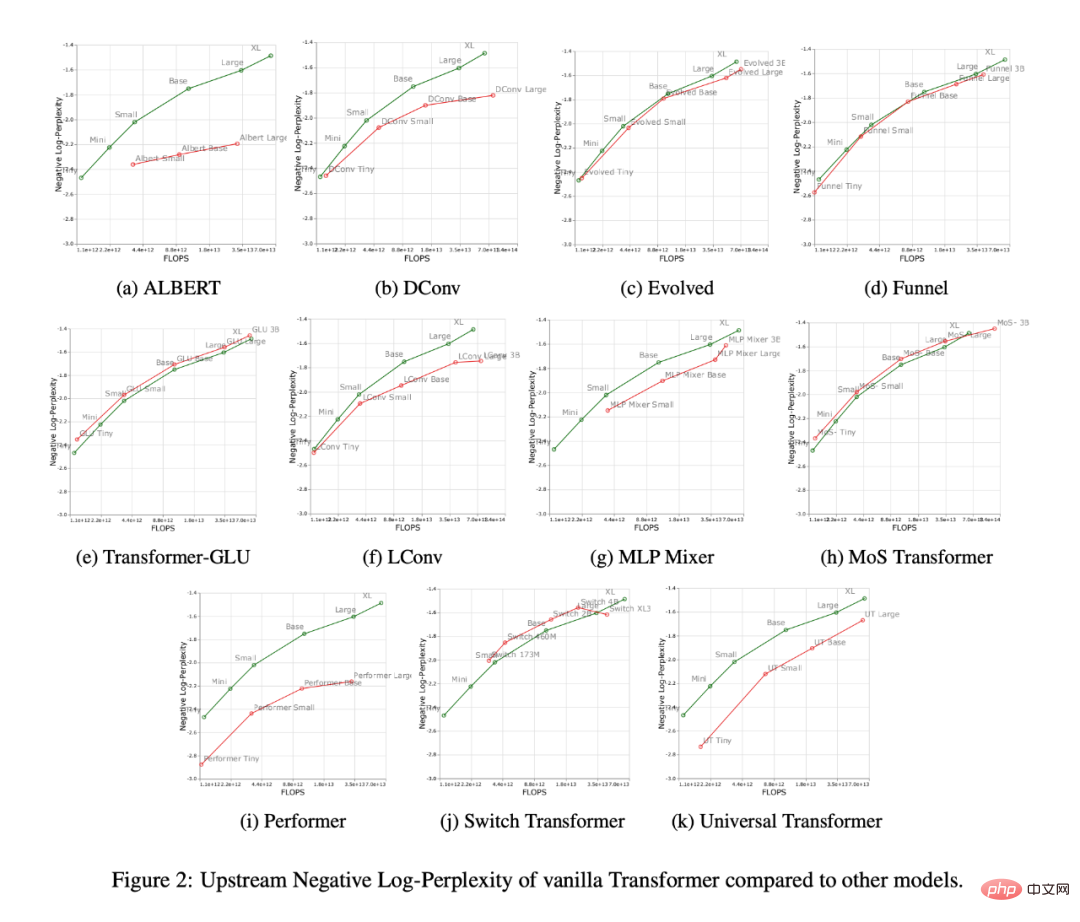
Figure 3 below shows the scaling curves of all models on the downstream migration task. It can be found that compared with Transformer, most models have different The scaling curve,changes significantly in downstream tasks. It is worth noting that most models have different upstream or downstream scaling curves.

The researchers found that some models, such as Funnel Transformer and LConv, seemed to perform quite well upstream, but were greatly affected downstream. As for Performer, the performance gap between upstream and downstream seems to be even wider. It is worth noting that the downstream tasks of SuperGLUE often require pseudo-cross-attention on the encoder, which models such as convolution cannot handle (Tay et al., 2021a).

Therefore, researchers have found that although some models have good upstream performance, they may still have difficulty learning downstream tasks.

#Is the best model different at each scale?

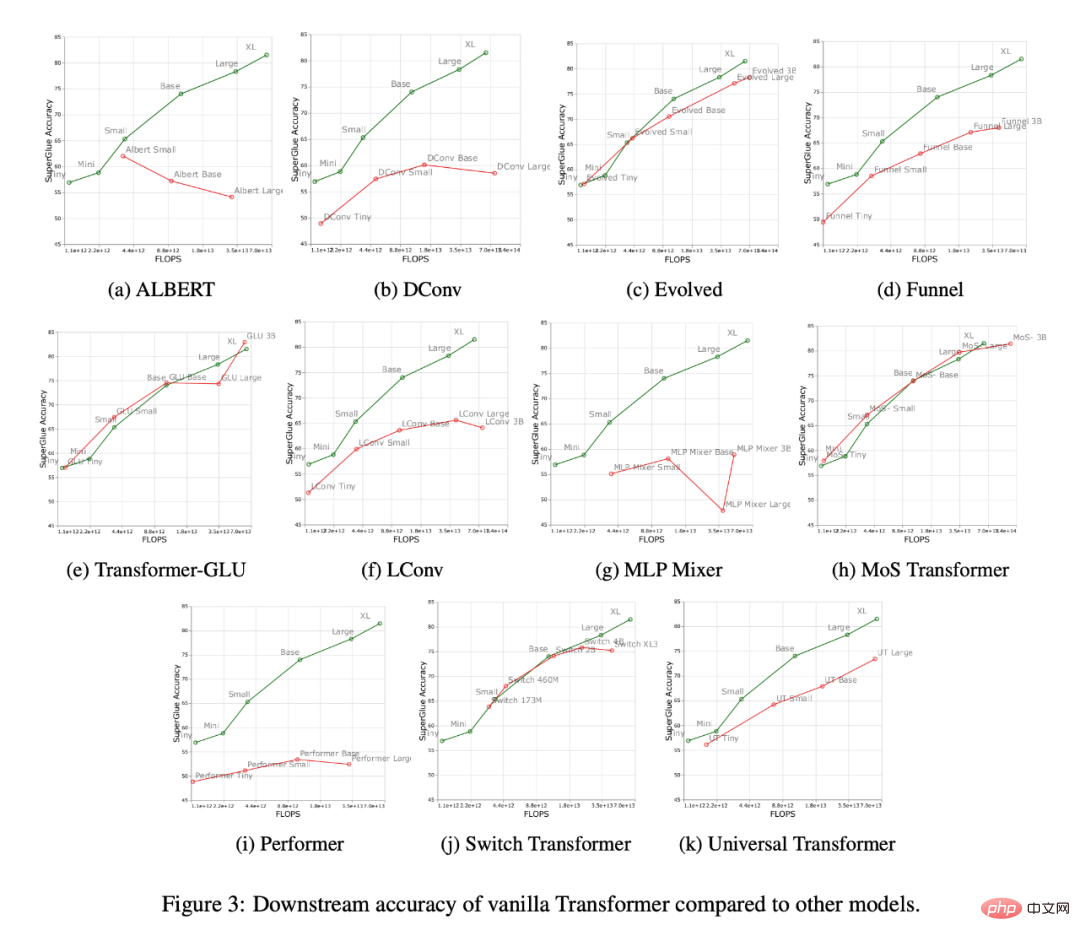
Figure 1 below shows the Pareto frontier when calculated in terms of upstream or downstream performance. The colors of the plot represent different models, and it can be observed that the best model may be different for each scale and calculation area. Additionally, this can also be seen in Figure 3 above. For example, the Evolved Transformer seems to perform just as well as the standard Transformer in the tiny to small region (downstream), but this changes quickly when scaling up the model. The researchers also observed this in MoS-Transformer, which performed significantly better than the ordinary Transformer in some areas, but not in other areas.

Scaling law of each model

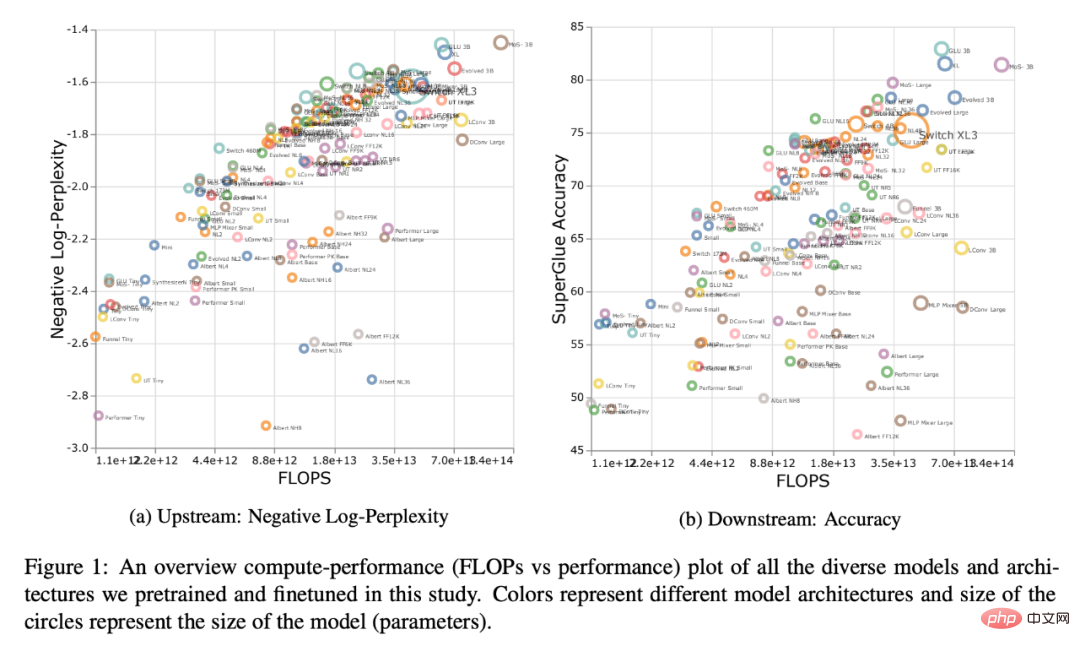
Table 2 below shows the fitting of each model in various situations The slope of the linear straight line α. The researchers obtained α by plotting F (FLOPs), U (upstream perplexity), D (downstream accuracy), and P (number of parameters). Generally speaking, α describes the scalability of the model, e.g. α_F,U plots FLOPs against upstream performance. The only exception is α_U,D, which is a measure of upstream and downstream performance, with high α_U,D values ​​meaning better model scaling to downstream tasks. Overall, the alpha value is a measure of how well a model performs relative to scaling.

Do Scaling Protocols affect model architecture in the same way?

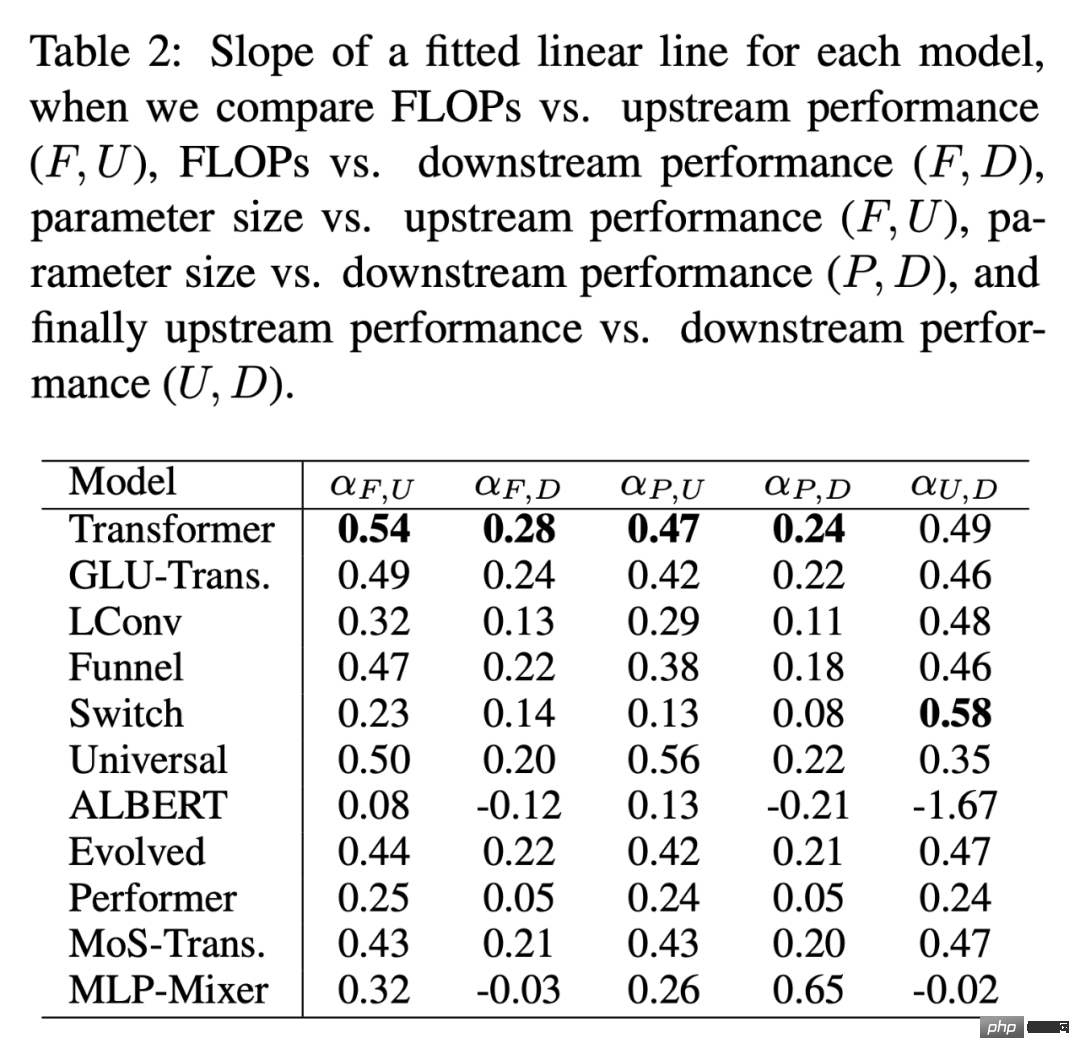
Figure 4 below shows the impact of scaling depth in four model architectures (MoS-Transformer, Transformer, Evolved Transformer, LConv).

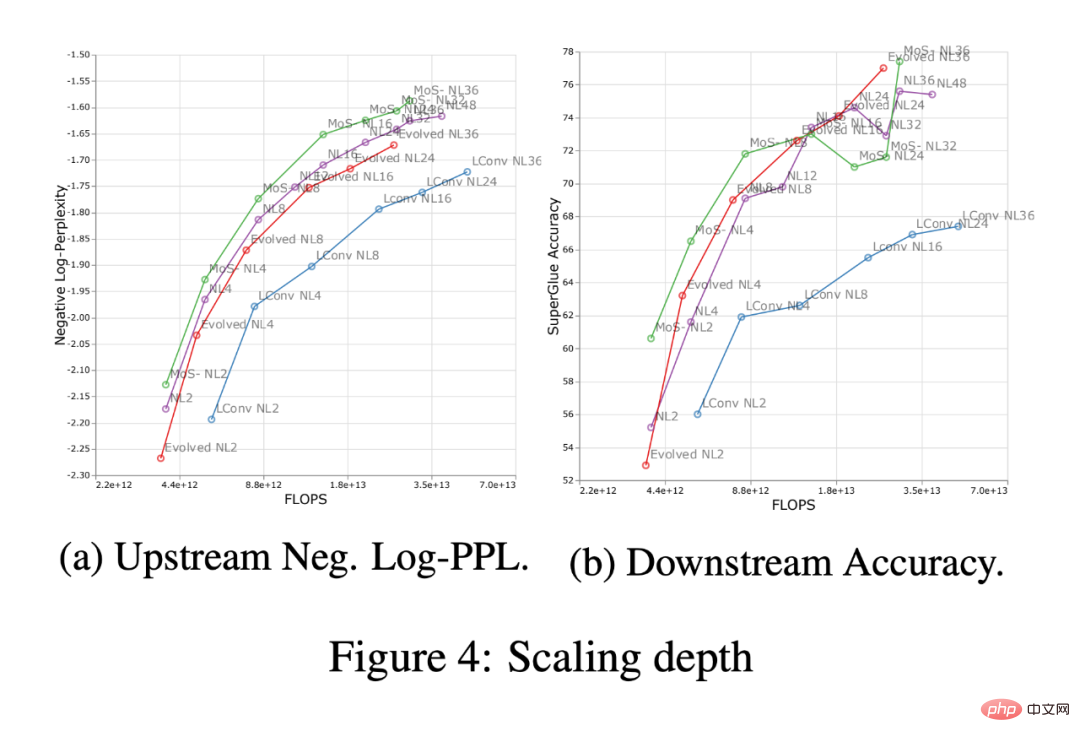
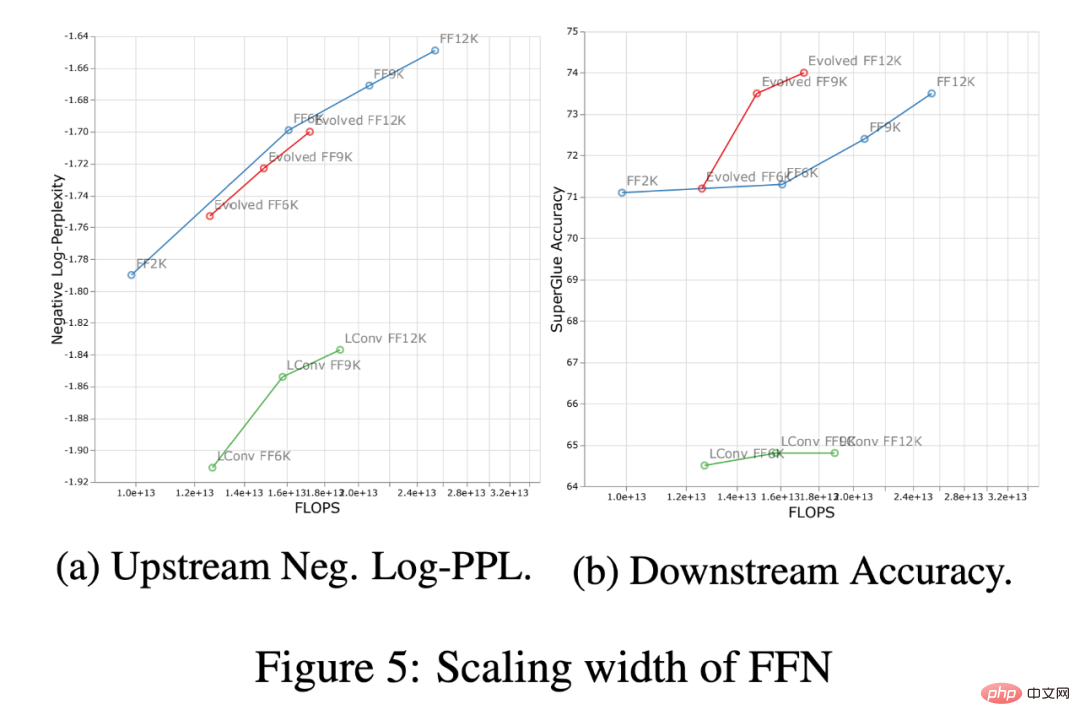
Figure 5 below shows the impact of scaling width across the same four architectures. First, on the upstream (negative log-perplexity) curve it can be noticed that although there are clear differences in absolute performance between different architectures, the scaling trends remain very similar. Downstream, with the exception of LConv, deep scaling (Figure 4 above) appears to work the same on most architectures. Also, it seems that the Evolved Transformer is slightly better at applying width scaling relative to width scaling. It is worth noting that depth scaling has a much greater impact on downstream scaling compared to width scaling.

For more research details, please refer to the original paper.

The above is the detailed content of New research from Google and DeepMind: How does inductive bias affect model scaling?. For more information, please follow other related articles on the PHP Chinese website!