A brief analysis of machine learning and differential equations

Although machine learning has been around since the 1950s, as computers have become more powerful and data has exploded, how can people use artificial intelligence to gain a competitive advantage, improve insights, and grow profits? Extensive practice. For different application scenarios, machine learning and differential equations have a wide range of scenarios.

Everyone has already used machine learning, especially deep learning based on neural networks. ChatGPT is very popular. Do you still need to understand differential equations in depth? No matter what the answer is, it will involve a comparison between the two. So, what is the difference between machine learning and differential equations?

Starting from the differential equation of the love model

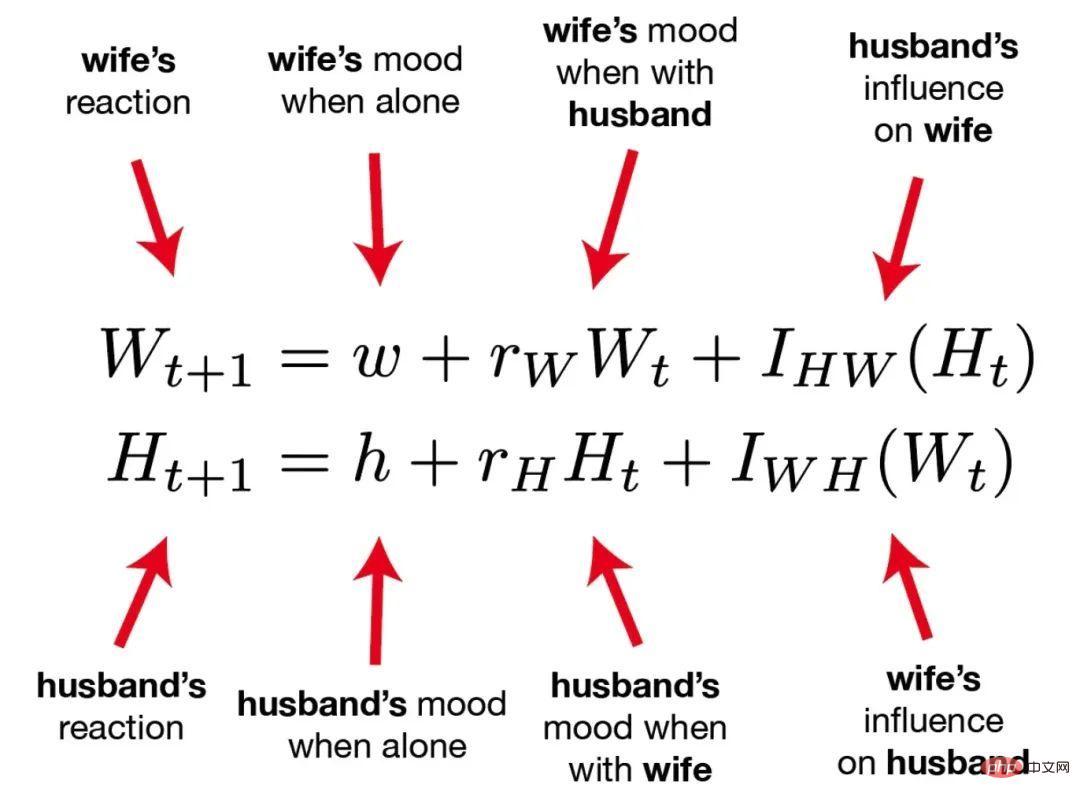
These two equations predict the longevity of the couple’s love relationship, based on psychology Based on the seminal work of psychologist John Gottman, the model predicts that sustained positive emotions are a powerful factor in marital success. For more interpretation of the model, you can refer to the book "Happy Marriage". The author also gives 7 rules for maintaining a happy marriage:

1. Perfect your love map
2. Cultivate affection and praise for your spouse
3. Move closer to each other instead of farther away
4. Let your spouse influence your decisions
5. Start with gentleness and end with compromise
6. Learn to live in harmony with problems
7. Create common meaning

We have experienced the epidemic personally for three years, and we know what is good and what is good. So, how to use differential equations to describe the relationship between patients and infectious persons?

#The SIR model assumes that viruses are spread through direct contact between infected and uninfected people, with sick people automatically recovering at some fixed rate.

These differential equations all contain the derivatives (ie, the rate of change) of some unknown functions. These unknown functions, such as S (t), I (t) and R (t) in the SIR model, are called the Solutions of differential equations. Based on the mechanics of these equations, we can derive how the model is designed, and the data will later be used to verify our hypotheses.

Classification of mathematical models

Mathematical models like differential equations make assumptions about the basic mechanism of the system in advance. Modeling begins with physics. In fact, the entire field of mathematical modeling begins with The 17th-century quest to unravel the fundamental dynamics behind planetary motion. Since then, mathematically based mechanistic models have unlocked key insights into many phenomena, from biology and engineering to economics and the social sciences. Such mechanism models can be divided into equation-based models, such as differential equations, or agent-based models.

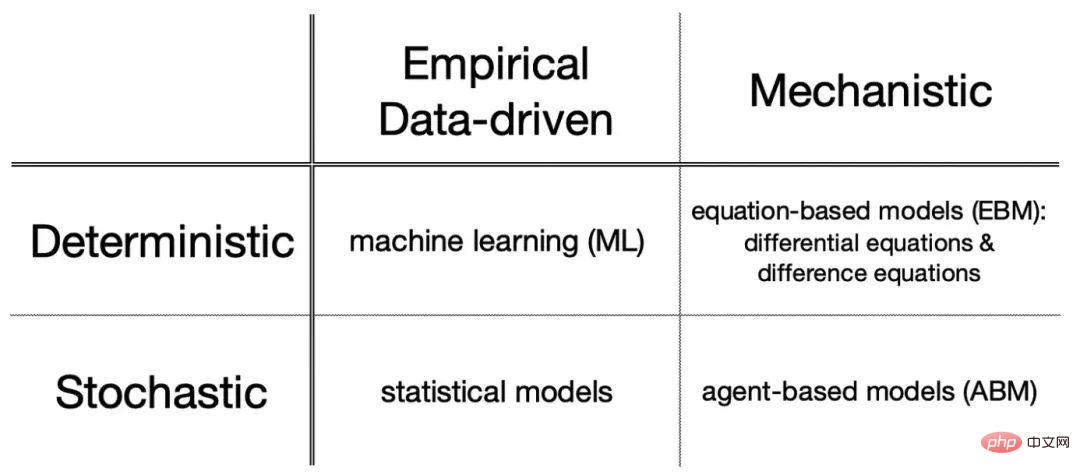
Experience-based or data-driven modeling, such as machine learning, is about understanding the structure of a system through rich data. Machine learning is especially useful for complex systems where we don't really know how to separate the signal from the noise, where simply training a clever algorithm can help solve the problem.

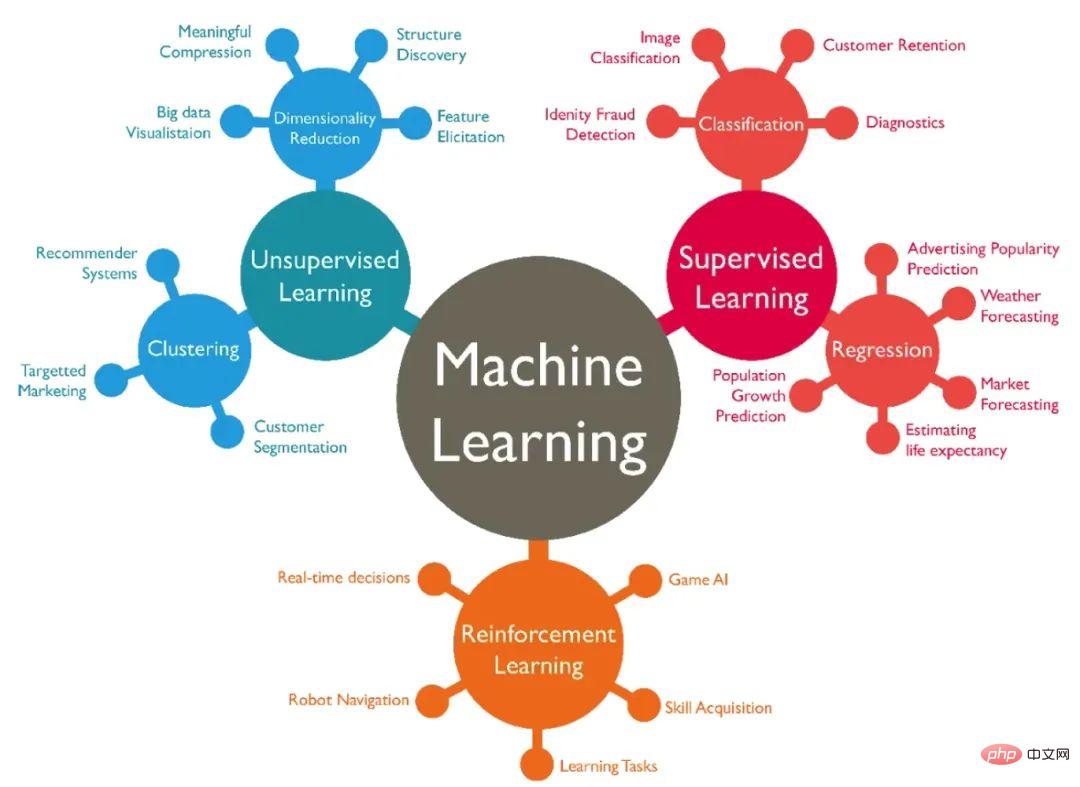
Machine learning tasks can be roughly divided into the following categories:

• Supervised learning (e.g., regression and classification);
• Unsupervised learning (e.g., Clustering and dimensionality reduction) ;
• Reinforcement Learning

Advanced machine learning and artificial intelligence systems are now everywhere in our daily lives No, from smart speaker-based conversational assistants (such as Xiaodu) to various recommendation engines, to facial recognition technology, and even Tesla’s self-driving cars. All of this is driven by mathematical and statistical modeling embedded beneath mountains of code.

Further, these models can be classified as "deterministic" (predictions are fixed) or "stochastic" (predictions include randomness).

Deterministic models ignore random variables and always predict the same results under the same starting conditions. In general, machine learning and equation-based models are deterministic and the output is always predictable. In other words, the output is completely determined by the input.

The stochastic model considers random changes in the population by introducing probability into the model. One way to capture these changes is to make each entity a separate Agent in the model, and define allowed behaviors and mechanisms for these agents, which have certain probabilities. These are Agent-based models.

However, the achievability of modeling individual actors comes at a cost, and agent-based models are more realistic. Due to the high computational cost and the interpretability of the model, this inspired a key concept in mathematical modeling: model complexity.

Model complexity

The dilemma of model complexity is a reality that all modelers must face. Our goal is to build and optimize both A model that is too simple and not too complex. Simple models are easy to analyze, but often lack predictive power. Complex models may be surreal, but it is possible to try to understand the truth behind complex problems.

We need to make a trade-off between simplicity and ease of analysis. Complex machine learning models strive to learn the signal (i.e., the true structure of the system) while rejecting the noise (i.e., interference). This causes the model to perform poorly on new data. In other words, machine learning models are less generalizable.

The delicate act of balancing model complexity is an "art", trying to find a sweet spot that is neither too simple nor too complex. This ideal model washes away the noise, captures the underlying dynamics of what is going on, and is reasonably explainable.

It should be noted that this means that a good mathematical model is not always correct. But that's okay. Generalizability is the goal, being able to explain to an audience why the model does what it does, whether they are academics, engineers, or business leaders.

All models are wrong, but some are useful. ——George Box, 1976

In machine learning and statistics, model complexity is called the bias-variance trade-off. High-bias models are too simple, resulting in underfitting, while high-variance models remember noise instead of signal, resulting in overfitting. Data scientists strive to achieve this delicate balance through careful selection of training algorithms and tuning of associated hyperparameters.

Comparison of Differential Equations and Machine Learning

In mechanism modeling, we carefully observe and review a system before making assumptions about the underlying mechanism of the system. phenomenon, and then validate the model with data. Are our assumptions correct? If so, since it is a hand-picked mechanism, it is entirely possible to explain to anyone what model behaves this way. If the assumption is wrong, that's okay, you just wasted some time, no big deal. Modeling is trial and error after all. Tinker with those assumptions or even start from scratch. Mechanism models, usually equations in the form of differential equations or even agent-based models.

In data-driven modeling, we first let the data start working and build a panoramic view of the system for us. All we have to do is meet the data quality of that machine and hopefully have enough data. This is machine learning. If a phenomenon is difficult for ordinary people to figure out, a machine can be tuned to sift through the noise and learn the elusive signal for us. Standard machine learning tasks include regression and classification, which are evaluated using a range of metrics. Neural networks and reinforcement learning have also become popular, enabling them to create models and learn surprisingly complex signals.

Although machine learning has been around since the 1950s, as computers have become more powerful and data has exploded, how can people use artificial intelligence to gain a competitive advantage, improve insights, and grow? Profits have launched a wide range of practices. For different application scenarios, machine learning and differential equations have a wide range of scenarios.

The above is the detailed content of A brief analysis of machine learning and differential equations. For more information, please follow other related articles on the PHP Chinese website!