
This article brings you relevant knowledge about javascript, which mainly introduces issues related to the implementation of the top ten sorting algorithms in JavaScript, including bubble sorting, selection sorting, insertion sorting, etc. If you have any other questions, let’s take a look at them below. I hope it will be helpful to everyone.

【Related recommendations: javascript video tutorial, web front-end】
The current solution is ascending order
Characteristics of bubble sorting , is processed one by one. The i-th number needs to be compared one by one with the subsequent len-i-1 numbers.
Why is the number of `len-i-1`?
Because the i numbers at the end of the array are already sorted, confirm that the position remains unchanged.
Why the confirmation position does not change? Because before they are fixed, they have been compared with the previous numbers one by one.
function bubbleSort(arr){
const len = arr.length;
for(let i = 0; i < len - 1; i++){
for(let j = 0; j < len - i - 1; j++){
if(arr[j] > arr[j+1]){
const tmp = arr[j+1];
arr[j+1] = arr[j];
arr[j] = tmp;
}
}
}
return arr;
}Quick sort uses the divide and conquer method idea.
By selecting a number as the comparison value, the other numbers to be sorted will be divided into two parts: >Comparison value and
function quickSort(arr){
sort(arr, 0, arr.length - 1);
return arr;
function sort(arr, low, high){
if(low >= high){
return;
}
let i = low;
let j = high;
const x = arr[i]; // 取出比较值x,当前位置i空出,等待填入
while(i < j){
// 从数组尾部,找出比x小的数字
while(arr[j] >= x && i < j){
j--;
}
// 将空出的位置,填入当前值, 下标j位置空出
// ps:比较值已经缓存在变量x中
if(i < j){
arr[i] = arr[j]
i++;
}
// 从数组头部,找出比x大的数字
while(arr[i] <= x && i < j){
i++;
}
// 将数字填入下标j中,下标i位置突出
if(i < j){
arr[j] = arr[i]
j--;
}
// 一直循环到左右指针i、j相遇,
// 相遇时,i==j, 所以下标i位置是空出的
}
arr[i] = x; // 将空出的位置,填入缓存的数字x,一轮排序完成
// 分别对剩下的两个区间进行递归排序
sort(arr, low, i - 1);
sort(arr, i+1, high);
}
}Hill sort It is an insertion sort algorithm. It is an improved and more efficient version of the simple insertion sort. Proposed by Donald Shell in 1959.
The feature is to use increment to divide the array into a group of subsequences, and then perform insertion sorting on the subsequences.
Since the increments decrease from large to small, it is also called shrinking increment sorting.
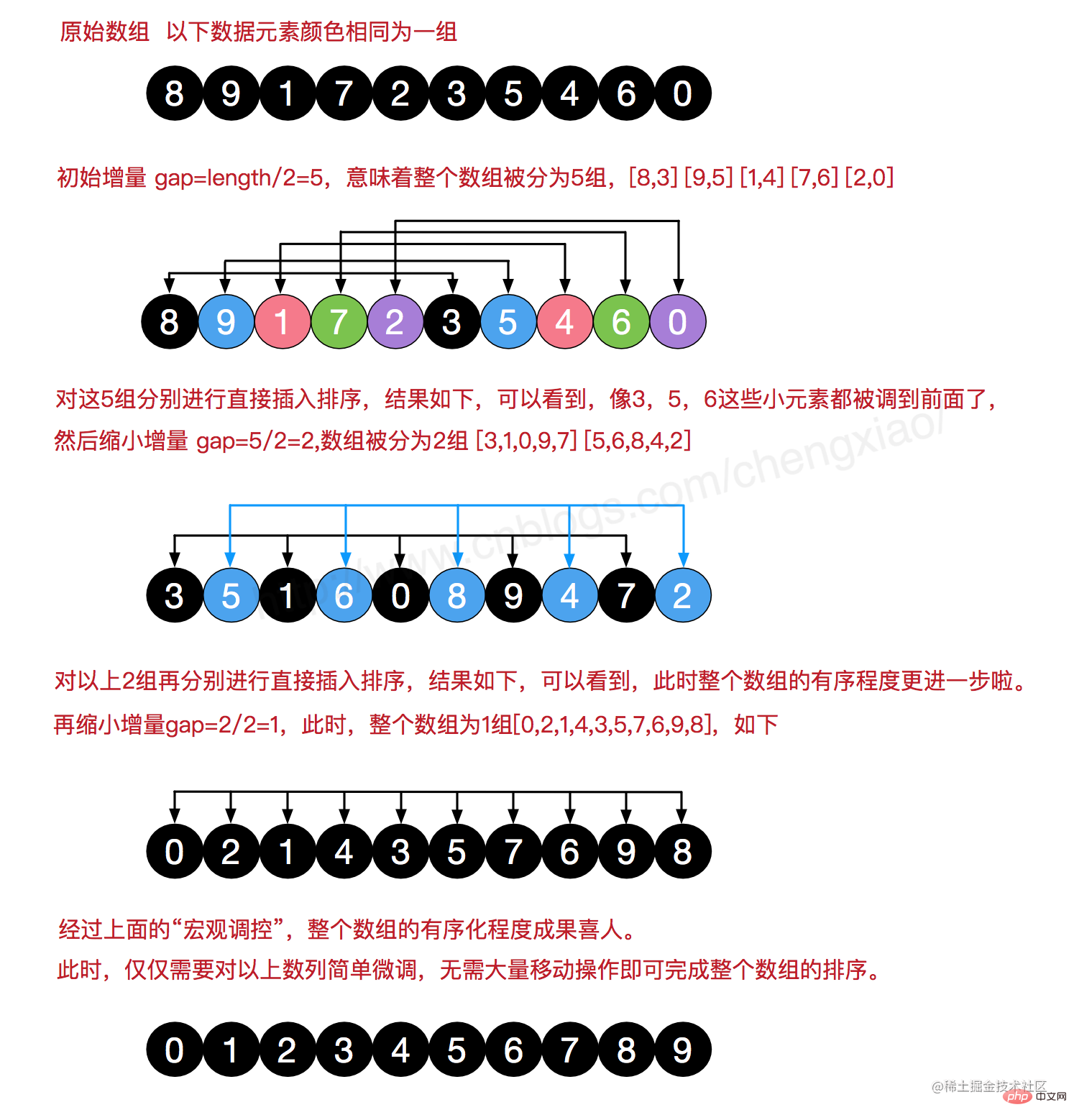
Notes
When insert sorting, it is not The numbers in a group are completed by insertion sort at once, but each group is interleaved.
When performing insertion, use the exchange method
function shellSort(arr){
// 分组规则 gap/2 递减
for(let gap = Math.floor(arr.length/2); gap > 0; gap = Math.floor(gap/2)){
for(let i = gap; i < arr.length; i++){
let j = i;
// 分组内数字,执行插入排序,
// 当下标大的数字,小于 下标小的数字,进行交互
// 这里注意,分组内的数字,并不是一次性比较完,需要i逐步递增,囊括下个分组内数字
while(j - gap >= 0 && arr[j] < arr[j - gap]){
swap(j, j-gap);
j = j - gap;
}
}
}
return arr;
function swap(a, b){
const tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
}When performing insertion, use the movement method
function shellSort(arr){
for(let gap = Math.floor(arr.length/2); gap > 0; gap = Math.floor(gap/2)){
for(let i = gap; i < arr.length; i++){
let j = i;
const x = arr[j]; // 缓存数字,空出位置
while(j - gap >= 0 && x < arr[j-gap]){
arr[j] = arr[j - gap]; // 将符合条件的数字,填入空出的位置
j = j - gap;
}
arr[j] = x; // 最后,将缓存的数字,填入空出的位置
}
}
return arr;
}
The current solution is ascending order
function selectionSort(arr){
const len = arr.length;
for(let i = 0; i < len-1; i++){
let minIndex = i;
for(let j = i+1; j < len; j++){
if(arr[j] < arr[minIndex]){
minIndex = j; // 保存最小数的下标
}
}
const tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
return arr;
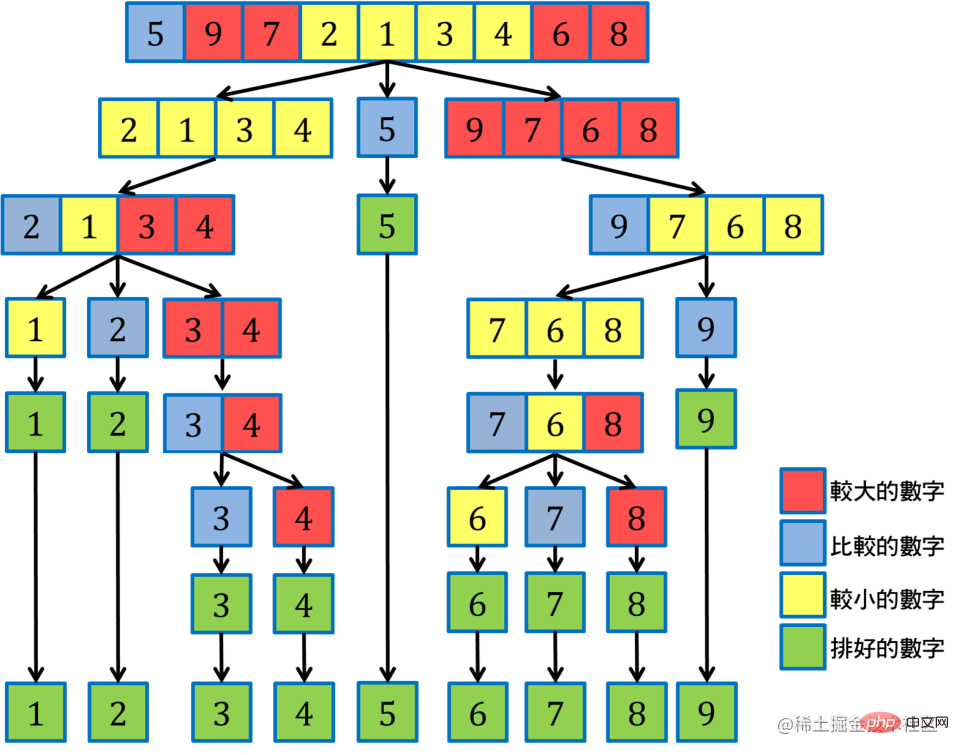
}Merge sorting uses the divide and conquer idea to decompose large arrays into small arrays until a single element. Then, use selective sorting to backtrack the split small arrays and merge them in order until they are merged into a large array.
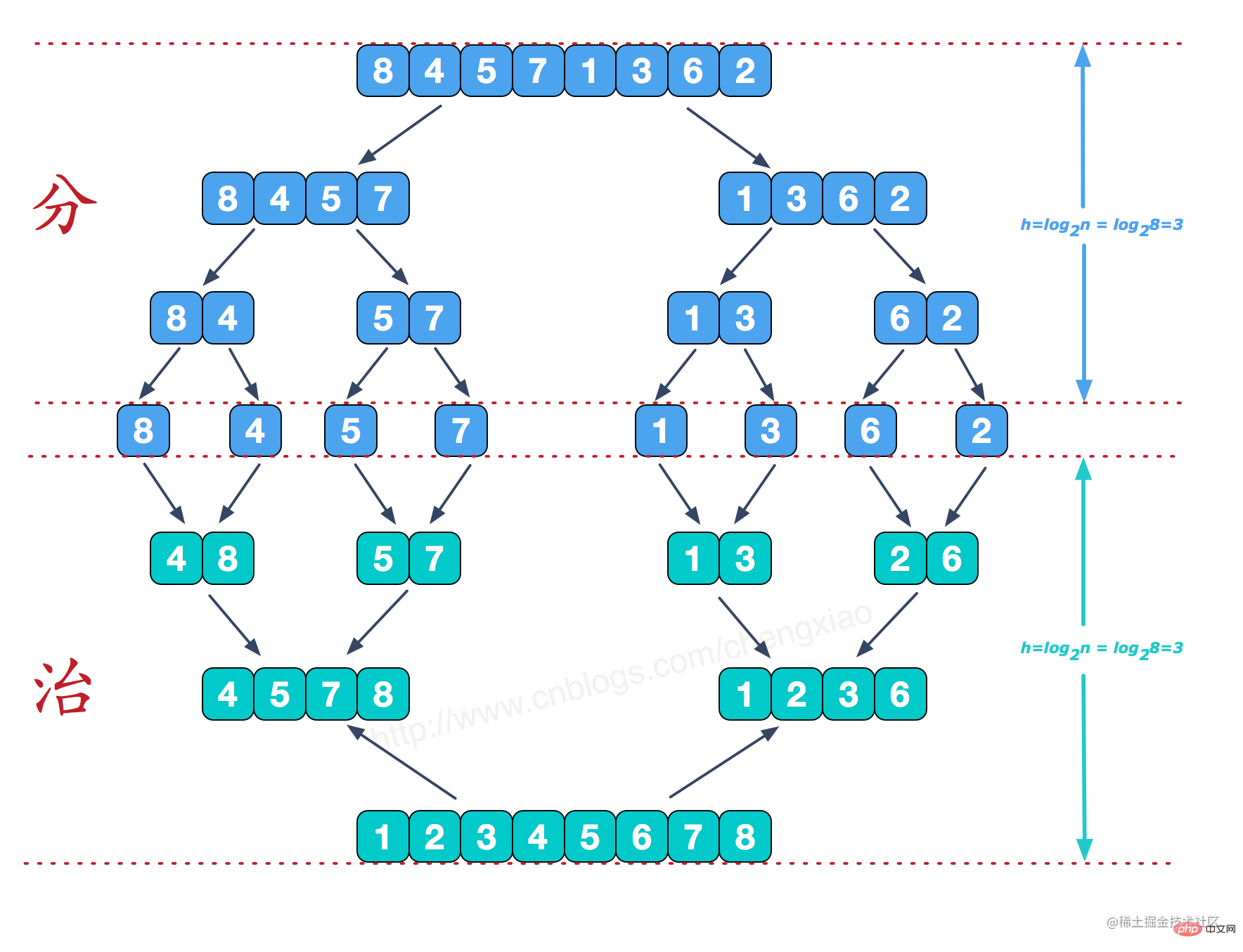
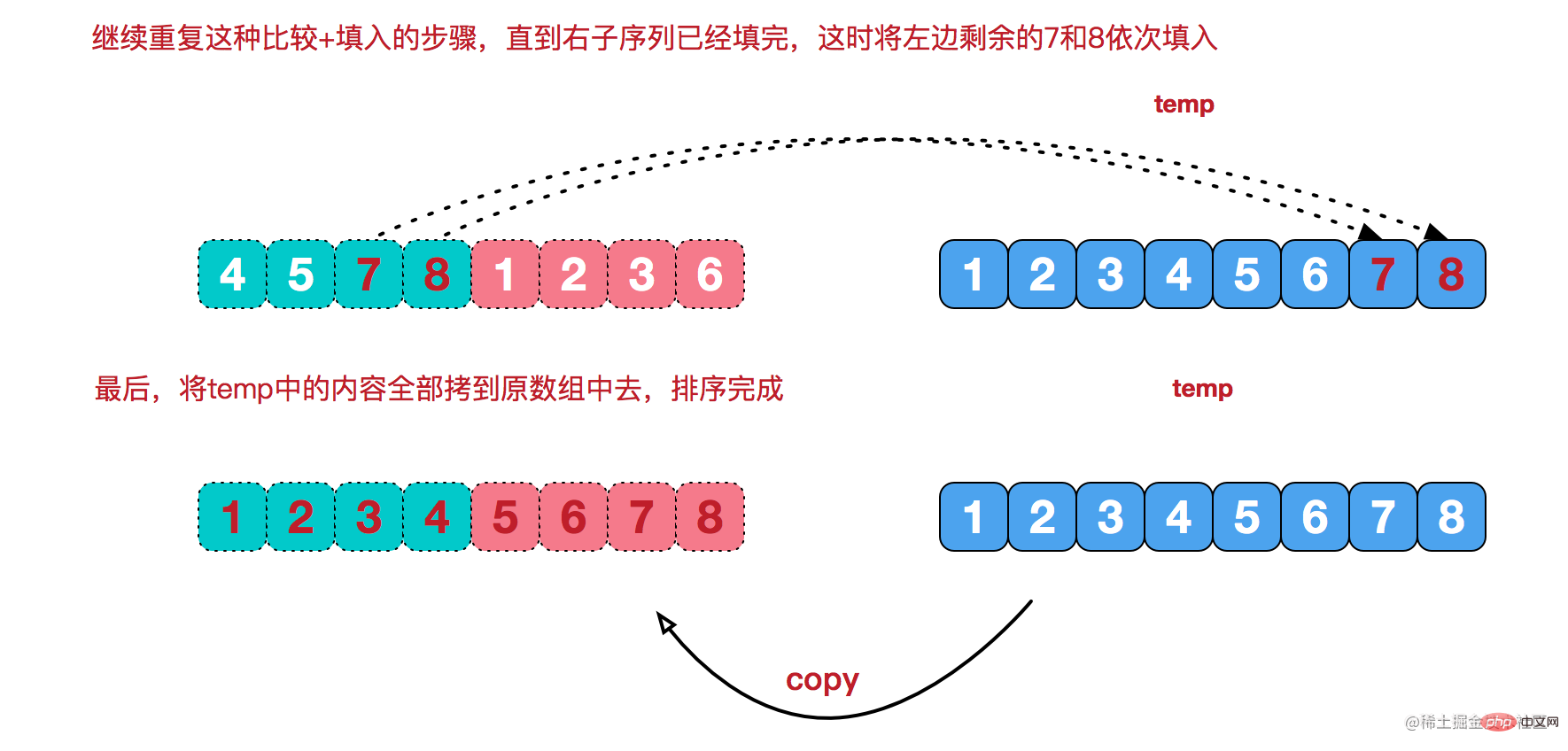
function mergeSort(arr){
return sort(arr, 0, arr.length - 1); // 注意右区间是arr.length - 1
// sort方法,进行递归
function sort(arr, left, right){
// 当left !== right时,证明还没分拆到最小元素
if(left < right){
// 取中间值,分拆为两个小的数组
const mid = Math.floor((left+right) / 2);
const leftArr = sort(arr, left, mid);
const rightArr = sort(arr, mid+1, right);
// 递归合并
return merge(leftArr, rightArr)
}
// left == right, 已经是最小元素,直接返回即可
return left >= 0 ? [arr[left]] : [];
}
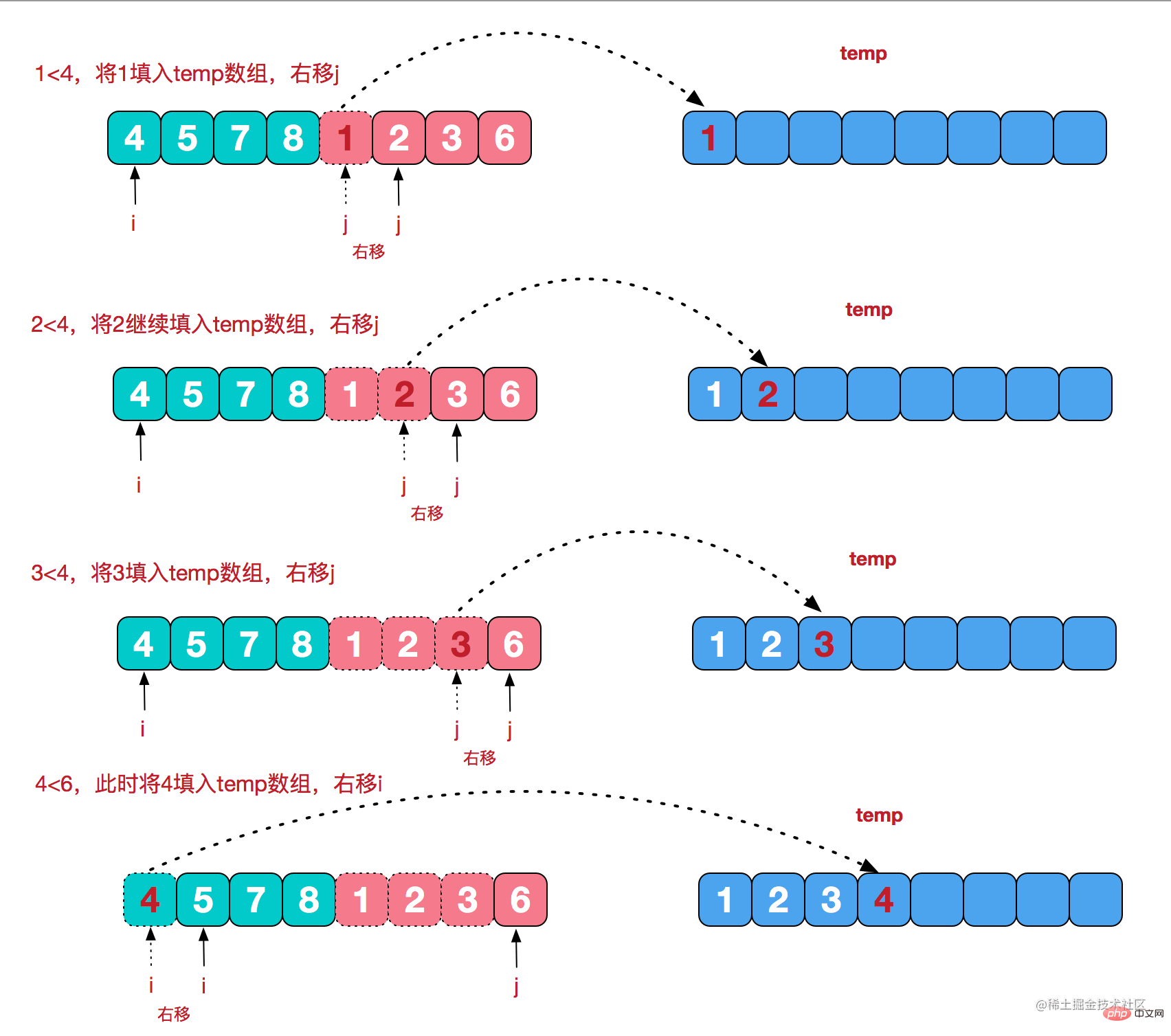
// 合并两个有序数组
function merge(leftArr, rightArr){
let left = 0;
let right = 0;
const tmp = [];
// 使用双指针,对两个数组进行扫描
while(left < leftArr.length && right < rightArr.length){
if(leftArr[left] <= rightArr[right]){
tmp.push(leftArr[left++]);
}else{
tmp.push(rightArr[right++]);
}
}
// 合并剩下的内容
if(left < leftArr.length){
while(left < leftArr.length){
tmp.push(leftArr[left++]);
}
}
if(right < rightArr.length){
while(right < rightArr.length){
tmp.push(rightArr[right++]);
}
}
return tmp;
}
}
The current solution is Ascending orderfunction insertionSort(arr){ const len = arr.length; // 注意,i 从 1 开始 for(let i = 1; i < len; i++){ let preIndex = i - 1; let current = arr[i]; // 位置i之前,是已排好序的数字,while的作用是找到一个坑位,给当前数字current插入 while(preIndex >= 0 && arr[preIndex] > current){ arr[preIndex+1] = arr[preIndex]; // 对大于current的值,往后移一位,给current的插入腾出位置 preIndex--; } arr[preIndex+1] = current; } return arr; }Heap sort<h2></h2>Summary<h3></h3> <blockquote>Heap representation<p></p> </blockquote> <p>Logical structure<strong> The representation is as follows: </strong></p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/a6068c5eefd9b1447a409043454b9e00-8.png"></p>The representation of <p> in the <strong> physical data layer is as follows: </strong></p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/405ed8621c7c2b8593e23df693916ec9-9.png"></p> Heap sort , is an optimized version of <p>selection sort<strong>, which uses the data structure - tree to manage data. </strong></p>Take the big top heap as an example: <p></p> <ul style="list-style-type: disc;"> <li>By constructing the big top heap<p></p> </li> <li>take out the maximum number on the top of the heap , exchange with the leaf nodes at the bottom of the heap<p></p> </li> <li>Then, the tree prunes off the maximum number of leaves<p></p> </li> <li>Then adjust the heap and change it again Create a big top heap<p></p> </li> <li>Return to step 2 and loop like this until all numbers are taken out<p></p> </li> </ul> <h3>效果图</h3> <blockquote><p>在实现代码时,构建大顶堆时,先保证左右子树的有序,再逐步扩大到整棵树。</p></blockquote> <p>构建大顶堆</p> <p>从第一个非叶子节点开始,调整它所在的子树</p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/405ed8621c7c2b8593e23df693916ec9-10.png"></p> <p>调整下标1节点的子树后,向上继续调整它的父节点(下标0)所在的子树</p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/f7d66106dbceae1059c0056d945ec9e5-11.png"></p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/f7d66106dbceae1059c0056d945ec9e5-12.png"></p> <p>最后,完成整个树的调整,构建好大顶堆。</p> <p>逐个抽出堆顶最大值</p> <p>堆顶数字与最末尾的叶子数字交换,抽出堆顶数字9。</p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/c463c70ccea56d283a5aa19b337fd7a6-13.png"></p> <p>此时,数字9位置固定下来,树剪掉9所在的叶子。然后,重新构建大顶堆。</p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/c463c70ccea56d283a5aa19b337fd7a6-14.png"></p> <p>大顶堆构建好后,继续抽出堆顶数字8,然后再次重新构建大顶堆。</p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/a2444ec5429c2b355c1a5c2db1cfe9bd-15.png"></p> <p>最后,所有节点抽出完成,代表排序已完成。</p> <p class="img-center"><img alt="" src="https://img.php.cn/upload/article/000/000/067/a2444ec5429c2b355c1a5c2db1cfe9bd-16.png"></p> <h3>解法</h3> <blockquote><p>以大顶堆为例,对数组进行升序排序</p></blockquote> <blockquote><p><strong>注意点</strong><br> 树的最后一个非叶子节点:<code>(arr.length / 2) - 1</code><br> 非叶子节点<code>i</code>的左叶子节点: <code>i*2+1</code><br> 非叶子节点<code>i</code>的右叶子节点: <code>i*2+2</code></p></blockquote> <pre class="brush:php;toolbar:false">function heapSort(arr){ // 初次构建大顶堆 for(let i = Math.floor(arr.length/2) - 1; i >= 0; i--){ // 开始的第一个节点是 树的最后一个非叶子节点 // 从构建子树开始,逐步调整 buildHeap(arr, i, arr.length); } // 逐个抽出堆顶最大值 for(let j = arr.length -1 ; j > 0; j--){ swap(arr, 0, j); // 抽出堆顶(下标0)的值,与最后的叶子节点进行交换 // 重新构建大顶堆 // 由于上一步的堆顶最大值已经交换到数组的末尾,所以,它的位置固定下来 // 剩下要比较的数组,长度是j,所以这里的值length == j buildHeap(arr, 0, j); } return arr; // 构建大顶堆 function buildHeap(arr, i, length){ let tmp = arr[i]; for(let k = 2*i+1; k < length; k = 2*k+1){ // 先判断左右叶子节点,哪个比较大 if(k+1 < length && arr[k+1] > arr[k]){ k++; } // 将最大的叶子节点,与当前的值进行比较 if(arr[k] > tmp){ // k节点大于i节点的值,需要交换 arr[i] = arr[k]; // 将k节点的值与i节点的值交换 i = k; // 注意:交换后,当前值tmp的下标是k,所以需要更新 }else{ // 如果tmp大于左右子节点,则它们的子树也不用判断,都是小于当前值 break; } } // i是交换后的下标,更新为tmp arr[i] = tmp; } // 交换值 function swap(arr, i, j){ const tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }Copy after login计数排序
概要
计数排序的要点,是开辟一块连续格子组成的空间,给数据进行存储。
将数组中的数字,依次读取,存入其值对应的下标中。
储存完成后,再按照空间的顺序,依次读取每个格子的数据,输出即可。所以,计数排序要求排序的数据,必须是有范围的整数。
效果图
解法
function countingSort(arr){ let maxValue = Number.MIN_VALUE; let minValue = Number.MAX_VALUE; let offset = 0; // 位移,用于处理负数 const result = []; // 取出数组的最大值, 最小值 arr.forEach(num => { maxValue = num > maxValue ? num : maxValue; minValue = num > minValue ? minValue : num; }); if(minValue < 0){ offset = -minValue; } const bucket = new Array(maxValue+offset+1).fill(0); // 初始化连续的格子 // 将数组中的每个数字,根据值放入对应的下标中, // `bucket[num] == n`格子的意义:存在n个数字,值为num arr.forEach(num => { bucket[num+offset]++; }); // 读取格子中的数 bucket.forEach((store, index) => { while(store--){ result.push(index - offset); } }); return result; }Copy after login桶排序
概要
桶排序是计数排序的优化版,原理都是一样的:分治法+空间换时间。
将数组进行分组,减少排序的数量,再对子数组进行排序,最后合并即可得到结果。效果图
解法
对桶内数字的排序,本文采用的是桶排序递归。其实它的本质是退化到计数排序。
function bucketSort(arr, bucketSize = 10){ // bucketSize 每个桶可以存放的数字区间(0, 9] if(arr.length <= 1){ return arr; } let maxValue = arr[0]; let minValue = arr[0]; let result = []; // 取出数组的最大值, 最小值 arr.forEach(num => { maxValue = num > maxValue ? num : maxValue; minValue = num > minValue ? minValue : num; }); // 初始化桶的数量 const bucketCount = Math.floor((maxValue - minValue)/bucketSize) + 1; // 桶的数量 // 初始化桶的容器 // 注意这里的js语法,不能直接fill([]),因为生成的二维下标数组,是同一个地址 const buckets = new Array(bucketCount).fill(0).map(() => []); // 将数字按照映射的规则,放入桶中 arr.forEach(num => { const bucketIndex = Math.floor((num - minValue)/bucketSize); buckets[bucketIndex].push(num); }); // 遍历每个桶内存储的数字 buckets.forEach(store => { // 桶内只有1个数字或者空桶,或者都是重复数字,则直接合并到结果中 if(store.length <= 1 || bucketSize == 1){ result = result.concat(store); return; } // 递归,将桶内的数字,再进行一次划分到不同的桶中 const subSize = Math.floor(bucketSize/2); // 减少桶内的数字区间,但必须是最少为1 const tmp = bucketSort(store, subSize <= 1 ? 1: subSize); result = result.concat(tmp); }); return result; }Copy after login基数排序
概述
基数排序,一般是从右到左,对进制位上的数字进行比较,存入[0, 9]的10个桶中,进行排序。
从低位开始比较,逐位进行比较,让每个进制位(个、十、百、千、万)上的数字,都能放入对应的桶中,形成局部有序。为什么10个桶?
因为十进制数,是由0-9数字组成,对应的进制位上的数字,都会落在这个区间内,所以是10个桶。
基数排序有两种方式:
MSD 从高位开始进行排序
LSD 从低位开始进行排序
效果图
解法
当前解法,只适用正整数的场景。
负数场景,需要加上偏移量解决。可参考 计数排序 的解法。function radixSort(arr){ let maxNum = arr[0]; // 求出最大的数字,用于确定最大进制位 arr.forEach(num => { if(num > maxNum){ maxNum = num; } }); // 获取最大数字有几位 let maxDigitNum = 0; while(maxNum > 0){ maxNum = Math.floor(maxNum / 10); maxDigitNum++; } // 对每个进制位上的数进行排序 for(let i = 0; i < maxDigitNum; i++){ let buckets = new Array(10).fill(0).map(() => []); // 初始化10个桶 for(let k = 0; k < arr.length; k++){ const bucketIndex = getDigitNum(arr[k], i); // 获取当前进制位上的数字 buckets[bucketIndex].push(arr[k]); // 排序的数字放入对应桶中 } // 所有数字放入桶中后,现从0-9的顺序将桶中的数字取出 const res = []; buckets.forEach(store => { store.forEach(num => { res.push(num); // 注意这里,先存入桶中的数字,先取出,这样才能保持局部有序 }) }); arr = res; } return arr; /** 求出数字每个进制位上的数字,只支持正整数 @param num 整数 @param digit 位数,从0开始 */ function getDigitNum(num, digit){ return Math.floor(num / Math.pow(10, digit) % 10) } }Copy after login算法复杂度
【相关推荐:javascript视频教程、web前端】
The above is the detailed content of JavaScript implements the top ten sorting algorithms (detailed explanation with pictures and text). For more information, please follow other related articles on the PHP Chinese website!