A ring counter composed of four flip-flops has at most several valid states.

The ring counter composed of four flip-flops has up to 16 states; the ring counter (D0=Qn(k-1)) is composed of a shift register plus a certain feedback circuit, a total of 16 There are only 4 valid counting states, and k D flip-flops have K counting states. If it is a twisted ring counter, there are 2K counting states, which is twice that of the ring.

The operating environment of this tutorial: Windows 10 system, DELL G3 computer.

The ring counter composed of four flip-flops has at most several valid states.

The ring counter (that is, D0=Qn(k-1)) has a total of 16 states, and the valid counting states are only 4, k D flip-flops have K counting states; if it is a twisted ring counter, there are 2K counting states, which is twice that of the ring.

The ring counter is composed of a shift register plus a certain feedback circuit. The shift register is used to form a general block diagram of a ring counter. It is composed of a shift register and a combined feedback logic circuit closed loop.

The output of the feedback circuit is connected to the serial input of the shift register. The input of the feedback circuit can be connected to the serial output of the shift register or some trigger depending on the type of shift register counter. the output terminal of the device.

Extended information

The ring counter is composed of a shift register plus a certain feedback circuit. The shift register is used to form a general block diagram of a ring counter. It is composed of a The shift register is composed of a closed loop of a combined feedback logic circuit. The output of the feedback circuit is connected to the serial input terminal of the shift register. The input terminal of the feedback circuit can be connected to the serial input terminal of the shift register according to the type of counter of the shift register. output or the output of some flip-flop.

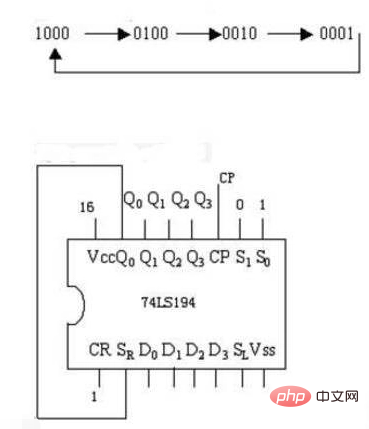
Introduction to working principle

Figure 23-5-2 is a four-bit ring counter, which is the lowest shift register The one-bit serial output terminal Q1 is fed back to the highest-order serial input terminal (that is, the data terminal of the D flip-flop). Ring counters are often used to realize the function of pulse sequence distribution (distributor). Assuming that the initial state of the register is [Q4Q3Q2Q1]=1000, then under the action of the shift pulse, its state will be converted in the sequence in Table 23-11.

When the third shift pulse arrives, Q1=1, which is fed back to the D4 input terminal. Under the action of the fourth shift pulse, Q4=1 and returns to the initial state. Each state in Table 23-11 will cycle through the four-bit shift register repeatedly under the action of the shift pulse.

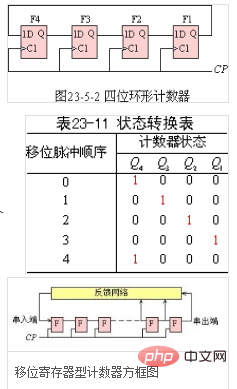
It can be seen from the above discussion that the counting length of the ring counting is N=n. Compared with the binary counter, it has 2^n-n states that are not used, and the effective states it uses are less.

For more related knowledge, please visit theFAQcolumn!

The above is the detailed content of A ring counter composed of four flip-flops has at most several valid states.. For more information, please follow other related articles on the PHP Chinese website!