

1. Introduction to Minimum Spanning Tree
What is a minimum spanning tree?
The minimum spanning tree (Minimum spanning tree, MST) is to find a tree T in a given undirected graph G(V,E), so that this tree has all the vertices in the graph G, And all edges are from edges in graph G, and satisfy the minimum sum of edge weights of the entire tree.
2.prim algorithm
is very similar to Dijkstra’s algorithm! ! Please look at the following Gif diagram. The core idea of the prim algorithm is to set a set S for the graph G (V, E), store the visited vertices, and then select the vertex with the smallest shortest distance from the set S each time from the set V-S ( Denoted as u), access and join the set S. Then, let the vertex u be the middle point, and optimize the shortest distance between all vertices v that can be reached from u and the set s. This operation is performed n times until the set s contains all vertices.
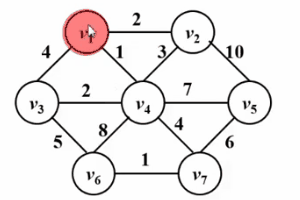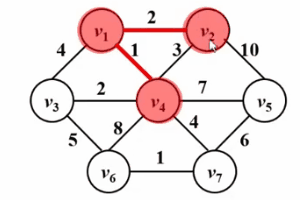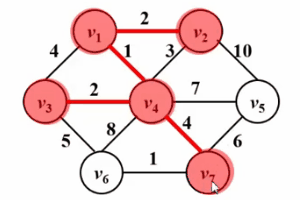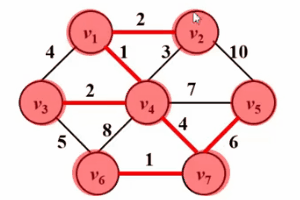
The difference is that dist in Dijkstra's algorithm is the shortest path from source point s to vertex w; while dist in prim's algorithm is from set S to vertex w The shortest path, the following is a comparison of their pseudocode descriptions. For a detailed description of the Dijkstra algorithm, please refer to the article

Algorithm implementation:
#include<iostream>
#include<vector>
#define INF 100000
#define MaxVertex 105
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int parent[MaxVertex]; // 并查集
int dist[MaxVertex]; // 距离
int Nv; // 结点
int Ne; // 边
int sum; // 权重和
using namespace std;
vector<Vertex> MST; // 最小生成树
// 初始化图信息
void build(){
Vertex v1,v2;
int w;
cin>>Nv>>Ne;
for(int i=1;i<=Nv;i++){
for(int j=1;j<=Nv;j++)
G[i][j] = 0; // 初始化图
dist[i] = INF; // 初始化距离
parent[i] = -1; // 初始化并查集
}
// 初始化点
for(int i=0;i<Ne;i++){
cin>>v1>>v2>>w;
G[v1][v2] = w;
G[v2][v1] = w;
}
}
// Prim算法前的初始化
void IniPrim(Vertex s){
dist[s] = 0;
MST.push_back(s);
for(Vertex i =1;i<=Nv;i++)
if(G[s][i]){
dist[i] = G[s][i];
parent[i] = s;
}
}
// 查找未收录中dist最小的点
Vertex FindMin(){
int min = INF;
Vertex xb = -1;
for(Vertex i=1;i<=Nv;i++)
if(dist[i] && dist[i] < min){
min = dist[i];
xb = i;
}
return xb;
}
void output(){
cout<<"被收录顺序:"<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<MST[i]<<" ";
cout<<"权重和为:"<<sum<<endl;
cout<<"该生成树为:"<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<parent[i]<<" ";
}
void Prim(Vertex s){
IniPrim(s);
while(1){
Vertex v = FindMin();
if(v == -1)
break;
sum += dist[v];
dist[v] = 0;
MST.push_back(v);
for(Vertex w=1;w<=Nv;w++)
if(G[v][w] && dist[w])
if(G[v][w] < dist[w]){
dist[w] = G[v][w];
parent[w] = v;
}
}
}
int main(){
build();
Prim(1);
output();
return 0;
}About the prim algorithm For a more detailed explanation, please refer to the video https://www.bilibili.com/video/av55114968?p=99
3.kruskal algorithm
Kruskal algorithm can also be used To solve the problem of minimum spanning tree, its algorithmic idea is easy to understand. Typical edge greedy, its algorithmic idea is:
● Hide all edges in the graph in the initial state, so that each vertex in the graph It is a single connected block, and there are n connected blocks in total
● Sort all edges according to edge weight from small to large
● Test all edges according to edge weight from small to large, if If the two vertices connected by the current test edge are not in the same connected block, then the test edge is added to the current minimum spanning tree, otherwise, the edge is discarded.
● Repeat the previous step until the number of edges in the minimum spanning tree is equal to the total number of vertices minus one or it ends when all edges are tested; if at the end, the number of edges in the minimum spanning tree is less than the total number of vertices minus one 1, indicating that the graph is not connected.
Please see the Gif below!
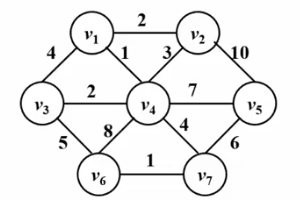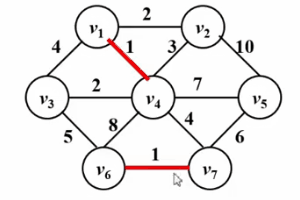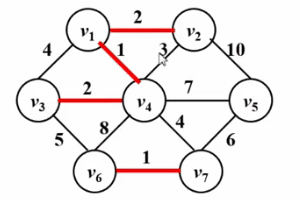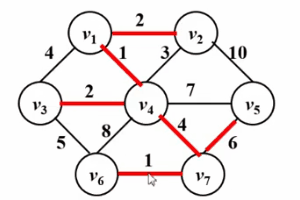
Algorithm implementation:
#include<iostream>
#include<string>
#include<vector>
#include<queue>
#define INF 100000
#define MaxVertex 105
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int parent[MaxVertex]; // 并查集最小生成树
int Nv; // 结点
int Ne; // 边
int sum; // 权重和
using namespace std;
struct Node{
Vertex v1;
Vertex v2;
int weight; // 权重
// 重载运算符成最大堆
bool operator < (const Node &a) const
{
return weight>a.weight;
}
};
vector<Node> MST; // 最小生成树
priority_queue<Node> q; // 最小堆
// 初始化图信息
void build(){
Vertex v1,v2;
int w;
cin>>Nv>>Ne;
for(int i=1;i<=Nv;i++){
for(int j=1;j<=Nv;j++)
G[i][j] = 0; // 初始化图
parent[i] = -1;
}
// 初始化点
for(int i=0;i<Ne;i++){
cin>>v1>>v2>>w;
struct Node tmpE;
tmpE.v1 = v1;
tmpE.v2 = v2;
tmpE.weight = w;
q.push(tmpE);
}
}
// 路径压缩查找
int Find(int x){
if(parent[x] < 0)
return x;
else
return parent[x] = Find(parent[x]);
}
// 按秩归并
void Union(int x1,int x2){
if(parent[x1] < parent[x2]){
parent[x1] += parent[x2];
parent[x2] = x1;
}else{
parent[x2] += parent[x1];
parent[x1] = x2;
}
}
void Kruskal(){
// 最小生成树的边不到 Nv-1 条且还有边
while(MST.size()!= Nv-1 && !q.empty()){
Node E = q.top(); // 从最小堆取出一条权重最小的边
q.pop(); // 出队这条边
if(Find(E.v1) != Find(E.v2)){ // 检测两条边是否在同一集合
sum += E.weight;
Union(E.v1,E.v2); // 并起来
MST.push_back(E);
}
}
}
void output(){
cout<<"被收录顺序:"<<endl;
for(Vertex i=0;i<Nv;i++)
cout<<MST[i].weight<<" ";
cout<<"权重和为:"<<sum<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<parent[i]<<" ";
cout<<endl;
}
int main(){
build();
Kruskal();
output();
return 0;
}For a more detailed explanation of the kruskal algorithm, please refer to the video https://www.bilibili.com/video/av55114968?p =100
Recommended course: C Language Tutorial
The above is the detailed content of Implementation of minimum spanning tree in c language. For more information, please follow other related articles on the PHP Chinese website!