
This time I will bring you a detailed explanation of an example of the sorting algorithm in the front-end. What are the precautions when using the sorting algorithm in the front-end. The following is a practical case, let's take a look.
The day before yesterday, I saw an article on Zhihu complaining about teacher Ruan Yifeng’s quick sorting algorithm. I would like to add a digression here. I think that no one can make mistakes without being a sage. I believe it. Books are not as good as no books. The process of learning is the process of constantly discovering and correcting mistakes. We should be happy when someone helps us correct this mistake, but I don’t think we should criticize Teacher Ruan Yifeng. He is also constantly learning and correcting mistakes. Growth, so everyone is the same, it doesn't matter if it is misleading, what if it is not him who makes the mistake, but a more powerful person? Where is the author of JavaScript? So everyone will make mistakes, we should also think more and be skeptical Accept it and always think about whether this is the optimal solution and whether there is a better solution. I think this is what we should do.
And I, as a front-end professional in computer science, cannot implement various tasks well. I felt very ashamed of the sorting algorithm based on this idea, so I took the time to carefully read the book "Data Structure and Algorithm Analysis: C Language Description Chinese Version.pdf>>This book, below I will make a summary of the sorting algorithms of various ideas that I understand. I hope it can give you some reference and gain. If there is anything wrong, please point it out. You can also share what you think is a better idea. I think everyone can learn together. Making progress together is the happiest thing~
(1) The concept of time complexity
Algorithm Time complexity is a function that qualitatively describes the running time of an algorithm. Big O notation is commonly used, excluding the low-order terms and high-order term coefficients of this function.
(2) Calculation method
Generally, the number of executions of basic operations in the algorithm is a function of the problem size n, represented by T(n). If there is an auxiliary function f(n), such that when n tends to When approaching infinity, the limit value of T(n)/f(n) is a non-zero constant, then f(n) is a function of the same order of magnitude as T(n), denoted as T(n) = O(f( n)), call O(f(n)) the asymptotic time complexity of the algorithm, referred to as time complexity.
Analysis: As module n increases at any time, the execution of the algorithm The growth rate of time is proportional to the growth rate of f(n), so the smaller f(n), the lower the time complexity of the algorithm, and the higher the efficiency of the algorithm.
When calculating the time complexity, first find out the basic operations of the algorithm, then calculate the number of executions of the basic operations, and find f(n) of the same order of magnitude as T(n) (its same order of magnitude generally has the following: 1, log₂n, n, nlog₂n, n squared, n cubed), if T(n) / f(n) finds the limit to obtain a constant c, then the time complexity T(n) = O(f(n)):
For example:
for(i = 1; i<p style="text-align: left;">We can get T(n) = n^3 n^2, and we can determine that n^3 is the same order of magnitude as T(n), f(n)=n^3; Then T(n) / f(n) = 1 1/n. The limit is constant 1, so the time complexity of this algorithm is: <br> T(n) = O(n ^3);</p><p style="text-align: left;"><strong>Note: For convenience, I will use N to represent the number of array elements.</strong></p><h1 style="text-align: left;">2. Sorting algorithm</h1><h2 style="text-align: left;">2.1 <a href="//m.sbmmt.com/code/12106.html" target="_blank">Bubble sorting</a>
</h2><h3 style="text-align: left;">2.1.1 Main idea:</h3><p style="text-align: left;">The main idea of bubble sorting is to traverse an array of length n, i starts from n -1 to 1, the maximum value of the first i elements of the array is placed at the i position. Imagine that the bubble sort is a vertical water column. The traversal process is that the large values (heavy ones) continue to sink, and the small ones continue to sink. The values (light ones) continue to float up, so that after the traversal is completed, the value at each position is larger than the previous value, and the sorting is completed.</p><h3 style="text-align: left;">2.1.2 Time complexity</h3><p style="text-align: left;">Most Time complexity in the bad case: o(n^2);<br>Time complexity in the best case: o(n^2);</p><h3 style="text-align: left;">2.1.3 Illustration of the sorting process:</h3> <p style="text-align: left;"><strong>The exit loop in the diagram is to exit the inner loop</strong><br><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/061/021/975255cd4031086ad718d4dc21df07d0-0.png" class="lazy" alt="Detailed explanation of sorting algorithm examples in front-end" title="Detailed explanation of sorting algorithm examples in front-end"></p><h3 style="max-width:90%">2.1.4 代码实现:</h3><h4 style="text-align: left;">冒泡排序-非递归实现</h4><pre class="brush:php;toolbar:false">function bubbleSort(arr) {
for(var i = arr.length - 1; i > 1; i--) {
for(var j=0; j arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr); // [8, 21, 32, 34, 51, 64]function bubbleSort(arr, n) {
if(n arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
return bubbleSort(arr, --n);
}
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr, arr.length); // [8, 21, 32, 34, 51, 64]插入排序有 n-1 趟排序组成,对于 i=1 到 i=n-1 趟,内层循环j从 i 到 1, 如果这其中有 j-1 位置上的元素大于 i 位置上的元素,就将该元素后移,知道条件不成立退出循环,这个时候大的值都被移动到后面了,j这个位置就是i位置上的元素应该在的位置.这样保证了每次循环i位置前的所有元素都是排好序的,新的循环就只需要 将 i 位置上的元素 和 j-1(也就是初始的 i-1) 位置上的元素作比较,如果大于则无需再往前比较,如果小于则继续往前比较后移.
最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n);
图解中的出循环是退出内层循环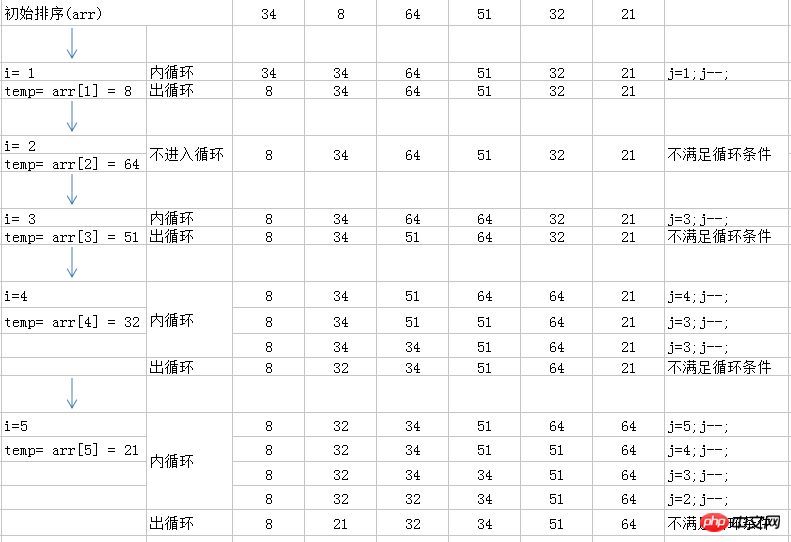
function insertSort(arr) {
var n = arr.length,temp = 0;
for(var i = 1; i 0 && arr[j-1] > temp; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr); // [8, 21, 32, 34, 51, 64]function insertSort(arr, n) {
if(n > 0 && n 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp;
i++;
return insertSort(arr, i);
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr, 1); // [8, 21, 32, 34, 51, 64]; // 这个函数的调用限定了第一次调用n的值只能传1顾名思义,快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(Nlog₂N).快速排序的关键在于枢纽元的选取,有一种比较推荐的选取方法就是选取左端的值,右端的值,中间位置的值(L(left + right) / 2)这三个数的中位数.举例: 输入为8,1,4,9,6,3,5,2,7,0, 左边元素8, 右边元素0,中间位置上的元素L(0+9)/2是4位置上的元素是6,L在表示向下取整.
8,0,6的中位数,先排序0,6,8, 这三个数的中位数是6.
通过一趟排序将要排序的部分分割成独立的两部分,其中一部分数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,依次达到整个数据变成有序序列.
第一步: 设置两个变量i,j,排序开始的时候: i=left,j=right-1,left和right分别表示要进行快速排序序列的起始索引和结束索引;
第二步: 从数组中随机选取一个元素,将其与arr[left]进行交换,即privot = arr[left],保证每一次的基准值都在序列的最左边;
第三步: 由j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于privot 的值arr[j],将arr[i]与arr[j]互换;
第四步: 从i开始向后搜索,即由前开始向后搜索(i++),找到一个大于privot 的arr[i],将arr[i]与arr[j]互换;
第五步: 重复第三步和第四步,直到不满足i
平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);

function quickSort(arr, left, right) {
if(left >= right) return;
var i = left;
var j = right - 1;
var privot = arr[left];
//console.log(privot);
while(i = privot) j--;
arr[i] = arr[j];
while(i<j var quicksort><h4 style="text-align: left;">快速排序-非递归实现</h4>
<pre class="brush:php;toolbar:false">function mainProduce(arr, left, right) {
var i = left, j = right - 1;
var rendomIndex = Math.floor(Math.random() * (j - i)) + left;
var temp = arr[left];arr[left] = arr[rendomIndex];arr[rendomIndex] = temp;
var privot = arr[left];
while(i = privot) j--;
var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
while(i<j> left + 1) {
s.push(left);s.push(mid);
}
if(mid left + 1) {
s.push(left);s.push(mid);
}
if(mid <h2 style="text-align: left;">2.4 希尔排序</h2>
<h3 style="text-align: left;">2.4.1 主要思想</h3>
<p style="text-align: left;">希尔排序是把记录按照下标的一定增量分组,对每组使用插入排序;随着增量逐渐减少,分割的数组越来越大,当增量减至1,整个<a href="//m.sbmmt.com/code/54.html" target="_blank">数组排序</a>完成,算法终止.</p>
<h3 style="text-align: left;">2.4.2主要步骤</h3>
<p style="text-align: left;">第一步: 选取一个增量d,初始值是Math.floor(len/2);<br>第二步: 然后将数组中间隔为增量d的组成新的分组,然后对这个分组的元素排序,完成排序后,增量除以2得到新的增量;<br>第三步: 重复第二步,直到增量为1,间隔为1的元素组成的分组就是整个数组,然后再对整个数组进行插入排序,得到最后排序后数组.</p>
<p style="text-align: left;">希尔排序是不稳定的,它在不断地交换的过程中会改变原来相等的元素的顺序.</p>
<h3 style="text-align: left;">2.4.3 时间复杂度</h3>
<p style="text-align: left;">平均情况下的时间复杂度: o(nlog₂n);<br>最好情况下的时间复杂度: o(n);</p>
<h3 style="text-align: left;">2.4.4 Detailed explanation of sorting algorithm examples in front-end</h3>
<p style="text-align: left;"><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/061/021/2f13ca0ab50333d1dad5851595e7225d-3.jpg" class="lazy" alt="Detailed explanation of sorting algorithm examples in front-end" title="Detailed explanation of sorting algorithm examples in front-end"></p>
<p style="text-align: left;">图片源于自百度百科: 图片来源</p>
<h3 style="text-align: left;">2.4.5 代码实现:</h3>
<h4 style="text-align: left;">希尔排序-递归实现</h4>
<pre class="brush:php;toolbar:false">function shellSort(arr, increment) {
var len = arr.length;
if(increment > 0) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
return shellSort(arr, Math.floor(increment/2));
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr, Math.floor(arr.length / 2));function shellSort(arr) {
var len = arr.length;
for(var increment = Math.floor(len / 2); increment > 0; increment = Math.floor(increment / 2)) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr);第一步: 将一个数组以中间值截取为为两个数组,分别将其排好序;
第二步: 申请一个空间,使其大小为两个已经排序的序列之和,该空间用来存放合并后的序列;
第三步: 设定两个指针,分别指向两个已排序序列的起始位置;
第四步: 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置.
重复第四步直到有一个某一指针超出序列尾;
将另一序列的所有元素复制到合并序列尾.
归并排序是稳定的,它在不会改变原来相等的元素的顺序.
平均情况下的时间复杂度: O(nlog₂n);
最好情况下的时间复杂度: O(nlog₂n) ;

var result = [];
function mergeArray(left, right) {
result = [];
while(left.length > 0 && right.length > 0) {
if(left[0] <p>相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!</p><p>推荐阅读:</p><p><a href="//m.sbmmt.com/js-tutorial-398003.html" target="_blank">React结合TypeScript和Mobx步骤详解</a><br></p><p><a href="//m.sbmmt.com/js-tutorial-398045.html" target="_blank">react实现选中li高亮步骤详解</a><br></p>The above is the detailed content of Detailed explanation of sorting algorithm examples in front-end. For more information, please follow other related articles on the PHP Chinese website!




