Implementation of Dijkstra's algorithm for the shortest path algorithm in Java-javaTutorial-php.cn

This article mainly introduces the Dijkstra algorithm that implements the shortest path algorithm in Java. The Dijkstra algorithm is a well-known shortest path algorithm. It is a single-start full-path algorithm. Those who are interested can learn more

Preface

Dijkstra's algorithm is a well-known shortest path algorithm and is a single-start full-path algorithm. This algorithm is called a successful example of "greedy algorithm". This article will try to introduce this great algorithm in the most popular language and give it Java implementation code.

1. Knowledge preparation:

1. Data structure representing the graph

is used There are many data structures for storing graphs. In this algorithm, the author uses an adjacency matrix.

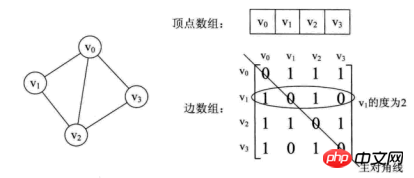
The adjacency matrix storage method of the graph is to use two arrays to represent the graph. A one-dimensional array stores vertex information in the graph, and a two-dimensional array (adjacency matrix) stores edge or arc information in the graph.

Suppose the graph G has n vertices, then the adjacency matrix is an n*n square matrix, defined as:

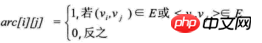
As can be seen from the above, the edge array of an undirected graph is a symmetric matrix. The so-called symmetric matrix means that the elements of the n-order matrix satisfy aij = aji. That is, the main diagonal from the upper left corner to the lower right corner of the matrix is the axis, and the elements in the upper right corner and the corresponding elements in the lower left corner are all equal.

From this matrix, it is easy to know the information in the picture.

(1) It is very easy to determine whether any two vertices have edges or no edges;

(2) To know the degree of a certain vertex, it is actually the degree of the vertex vi in the adjacency matrix. The sum of the elements in the i row or (i-th column);

(3) To find all the adjacent points of the vertex vi is to scan the i-th row elements in the matrix, and arc[i][j] is 1. Adjacent points;

And directed graphs pay attention to in-degree and out-degree. The in-degree of vertex vi is 1, which is exactly the sum of the numbers in the i-th column. The out-degree of vertex vi is 2, which is the sum of the numbers in the i-th row.

The definition of directed graph is also similar, so no details will be given.

2. Single starting point full path

The so-called single starting point full path refers to the shortest path starting from a starting point to all nodes in a graph.

3. Basic knowledge of graph theory (readers need to find relevant information by themselves)

4. Complementary relaxation conditions

Suppose the scalar d1, d2,....,dN satisfies

dj<=di + aij, (i,j) belongs to A,

and P has i1 as the starting point and ik as the end point path, if

dj = di + aij,

is true for all edges (i, j) of P, then P is the shortest path from i1 to ik. Among them, the complementary relaxation conditions of the shortest path problem that satisfy the above two equations are called.

2. Algorithm idea

1. Let G = (V, E) be a weighted undirected graph. If there are two adjacent nodes in G, i and j. aij (expressed as a subscript here and later, please note) is the weight from node i to node j, which can be understood as the distance in this algorithm. Each node has a value di (node label) indicating its distance from the starting point to a certain path to it.

2. The algorithm initially has an array V used to store a list of unvisited nodes, which we temporarily call the candidate list. Select node 1 as the starting node. At the beginning, d1=0 for node 1, di=infinity for other nodes, and V is all nodes.
After initializing the conditions, then start the iterative algorithm and stop when V is the empty set. The specific iteration steps are as follows:

Remove the node di with the smallest d value from the candidate list. (In this example, the data structure of V uses a priority queue to implement the minimum value dequeue. It is best to use Fibonacci pairs, which have been introduced in previous articles, and the performance is greatly improved). For every edge starting from this node, excluding the node where V is removed, (i, j) belongs to A. If dj > di + aij (violating the relaxation condition), then let

dj = di + aij , (if j has been removed from V, it means that its minimum distance has been calculated and does not participate in this calculation)

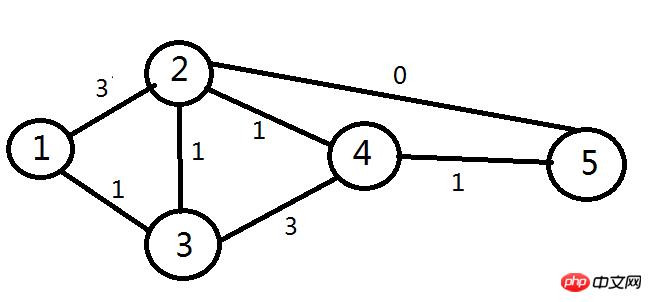
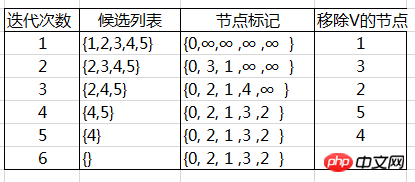
It can be seen that in the calculation project of the algorithm, the d value of the node is The specific algorithm diagram of the monotonous and non-increasing

is as follows

3. Java code implementation

public class Vertex implements Comparable<Vertex>{

  /**
   * 节点名称(A,B,C,D)
   */
  private String name;
  
  /**
   * 最短路径长度
   */
  private int path;
  
  /**
   * 节点是否已经出列(是否已经处理完毕)
   */
  private boolean isMarked;
  
  public Vertex(String name){
    this.name = name;
    this.path = Integer.MAX_VALUE; //初始设置为无穷大
    this.setMarked(false);
  }
  
  public Vertex(String name, int path){
    this.name = name;
    this.path = path;
    this.setMarked(false);
  }
  
  @Override
  public int compareTo(Vertex o) {
    return o.path > path?-1:1;
  }
}

Copy after login

public class Graph {

  /*
   * 顶点
   */
  private List<Vertex> vertexs;

  /*
   * 边
   */
  private int[][] edges;

  /*
   * 没有访问的顶点
   */
  private Queue<Vertex> unVisited;

  public Graph(List<Vertex> vertexs, int[][] edges) {
    this.vertexs = vertexs;
    this.edges = edges;
    initUnVisited();
  }
  
  /*
   * 搜索各顶点最短路径
   */
  public void search(){
    while(!unVisited.isEmpty()){
      Vertex vertex = unVisited.element();
      //顶点已经计算出最短路径，设置为"已访问"
     　　vertex.setMarked(true);  
      //获取所有"未访问"的邻居
      　　List<Vertex> neighbors = getNeighbors(vertex);  
      //更新邻居的最短路径
      updatesDistance(vertex, neighbors);    
      pop();
    }
    System.out.println("search over");
  }
  
  /*
   * 更新所有邻居的最短路径
   */
  private void updatesDistance(Vertex vertex, List<Vertex> neighbors){
    for(Vertex neighbor: neighbors){
      updateDistance(vertex, neighbor);
    }
  }
  
  /*
   * 更新邻居的最短路径
   */
  private void updateDistance(Vertex vertex, Vertex neighbor){
    int distance = getDistance(vertex, neighbor) + vertex.getPath();
    if(distance < neighbor.getPath()){
      neighbor.setPath(distance);
    }
  }

  /*
   * 初始化未访问顶点集合
   */
  private void initUnVisited() {
    unVisited = new PriorityQueue<Vertex>();
    for (Vertex v : vertexs) {
      unVisited.add(v);
    }
  }

  /*
   * 从未访问顶点集合中删除已找到最短路径的节点
   */
  private void pop() {
    unVisited.poll();
  }

  /*
   * 获取顶点到目标顶点的距离
   */
  private int getDistance(Vertex source, Vertex destination) {
    int sourceIndex = vertexs.indexOf(source);
    int destIndex = vertexs.indexOf(destination);
    return edges[sourceIndex][destIndex];
  }

  /*
   * 获取顶点所有(未访问的)邻居
   */
  private List<Vertex> getNeighbors(Vertex v) {
    List<Vertex> neighbors = new ArrayList<Vertex>();
    int position = vertexs.indexOf(v);
    Vertex neighbor = null;
    int distance;
    for (int i = 0; i < vertexs.size(); i++) {
      if (i == position) {
        //顶点本身，跳过
        continue;
      }
      distance = edges[position][i];  //到所有顶点的距离
      if (distance < Integer.MAX_VALUE) {
        //是邻居(有路径可达)
        neighbor = getVertex(i);
        if (!neighbor.isMarked()) {
          //如果邻居没有访问过，则加入list;
          neighbors.add(neighbor);
        }
      }
    }
    return neighbors;
  }

  /*
   * 根据顶点位置获取顶点
   */
  private Vertex getVertex(int index) {
    return vertexs.get(index);
  }

  /*
   * 打印图
   */
  public void printGraph() {
    int verNums = vertexs.size();
    for (int row = 0; row < verNums; row++) {
      for (int col = 0; col < verNums; col++) {
        if(Integer.MAX_VALUE == edges[row][col]){
          System.out.print("X");
          System.out.print(" ");
          continue;
        }
        System.out.print(edges[row][col]);
        System.out.print(" ");
      }
      System.out.println();
    }
  }
}

Copy after login

public class Test {

  public static void main(String[] args){
    List<Vertex> vertexs = new ArrayList<Vertex>();
    Vertex a = new Vertex("A", 0);
    Vertex b = new Vertex("B");
    Vertex c = new Vertex("C");
    Vertex d = new Vertex("D");
    Vertex e = new Vertex("E");
    Vertex f = new Vertex("F");
    vertexs.add(a);
    vertexs.add(b);
    vertexs.add(c);
    vertexs.add(d);
    vertexs.add(e);
    vertexs.add(f);
    int[][] edges = {
        {Integer.MAX_VALUE,6,3,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {6,Integer.MAX_VALUE,2,5,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {3,2,Integer.MAX_VALUE,3,4,Integer.MAX_VALUE},
        {Integer.MAX_VALUE,5,3,Integer.MAX_VALUE,5,3},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,4,5,Integer.MAX_VALUE,5},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,3,5,Integer.MAX_VALUE}
    
    };
    Graph graph = new Graph(vertexs, edges);
    graph.printGraph();
    graph.search();
  }
  
}

Copy after login

The above is the detailed content of Implementation of Dijkstra's algorithm for the shortest path algorithm in Java. For more information, please follow other related articles on the PHP Chinese website!