Detailed example of Python solving optimal job scheduling based on backtracking subset tree template

This article mainly introduces Python to solve the optimal job scheduling problem based on the backtracking method subset tree template. It briefly explains the job scheduling problem and combines it with examples to give Python's solution to the optimal job scheduling problem using the backtracking method subset tree template. For specific steps and related operating skills, friends in need can refer to

This article describes an example of how Python solves the optimal job scheduling problem based on the backtracking method subset tree template. Share it with everyone for your reference, the details are as follows:

Question

Given n jobs, each job has two subtasks It needs to be done on two machines respectively. Each job must be processed first by Machine 1 and then by Machine 2.

Try to design an algorithm to find the best schedule to complete these n tasks, so that the sum of the time for machine 2 to complete each job can be minimized.

Analysis:

Look at a specific example:

tji Machine 1 Machine 2
Job 1 2 1
Job 2 3 1
Job 3 2 3

Optimal scheduling order: 1 3 2

Processing time: 18

6 of these 3 jobs The possible scheduling plans are 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,1,2; 3,2,1;

They all The corresponding completion times are 19, 18, 20, 21, 19, and 19 respectively. It is easy to see that the optimal scheduling plan is 1,3,2, and the sum of its completion times is 18.

Take 1, 2, 3 as an example:

The completion time of job 1 on machine 1 is 2, and the completion time on machine 2 is 3
The completion time of job 2 on machine 1 is 5, and the completion time on machine 2 is 6
The completion time of job 3 on machine 1 is 7, and the completion time on machine 2 is 10
3+6+10 = 19

1, 3, 2

The completion time of job 1 on machine 1 is 2, and on machine 2 The completion time of job 3 is 3 on machine 1, and the completion time of job 3 on machine 2 is 7.
The completion time of job 2 on machine 1 is 7, and it is completed on machine 2. The time is 8

3+7+8 = 18

Code

'''
最佳作业调度问题
tji     机器1   机器2
作业1     2     1
作业2     3     1
作业3     2     3
'''
n = 3 # 作业数
# n个作业分别在两台机器需要的时间
t = [[2,1],
   [3,1],
   [2,3]]
x = [0]*n  # 一个解（n元数组，xi∈J）
X = []   # 一组解
best_x = [] # 最佳解（一个调度）
best_t = 0 # 机器2最小时间和
# 冲突检测
def conflict(k):
  global n, x, X, t, best_t
  # 部分解内的作业编号x[k]不能超过1
  if x[:k+1].count(x[k]) > 1:
    return True
  # 部分解的机器2执行各作业完成时间之和未有超过 best_t
  #total_t = sum([sum([y[0] for y in t][:i+1]) + t[i][1] for i in range(k+1)])
  j2_t = []
  s = 0
  for i in range(k+1):
    s += t[x[i]][0]
    j2_t.append(s + t[x[i]][1])
  total_t = sum(j2_t)
  if total_t > best_t > 0:
    return True
  return False # 无冲突
# 最佳作业调度问题
def dispatch(k): # 到达第k个元素
  global n, x, X, t, best_t, best_x
  if k == n: # 超出最尾的元素
    #print(x)
    #X.append(x[:]) # 保存（一个解）
    # 根据解x计算机器2执行各作业完成时间之和
    j2_t = []
    s = 0
    for i in range(n):
      s += t[x[i]][0]
      j2_t.append(s + t[x[i]][1])
    total_t = sum(j2_t)
    if best_t == 0 or total_t < best_t:
      best_t = total_t
      best_x = x[:]
  else:
    for i in range(n): # 遍历第k个元素的状态空间，机器编号0~n-1，其它的事情交给剪枝函数
      x[k] = i
      if not conflict(k): # 剪枝
        dispatch(k+1)
# 测试
dispatch(0)
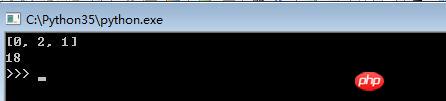
print(best_x) # [0, 2, 1]
print(best_t) # 18

Rendering

The above is the detailed content of Detailed example of Python solving optimal job scheduling based on backtracking subset tree template. For more information, please follow other related articles on the PHP Chinese website!