
This article first explains the operations corresponding to pooling, then analyzes some of the principles behind pooling, and finally gives the Python implementation of pooling.
1. Operations corresponding to pooling
First of all, we have an intuitive concept of pooling as a whole (that is, describing the input, output and specific functions of pooling, but ignoring the specific implementation details): The input of pooling is a Matrix, the output is a matrix; the completed function is to operate on a local area of the input matrix so that the output corresponding to the area can best represent the characteristics of the area. As shown in Figure 1, the yellow matrix on the left represents the input matrix, and the blue matrix on the right represents the output matrix; the dynamic orange matrix represents a local area of the selected input matrix, and then finds the best representative of the area, and finally All selected representatives are sorted in the output matrix according to the spatial position relationship corresponding to the original input matrix.
This process can be compared to the election process. If you want to elect the mayor of Beijing, a feasible approach is for each district in Beijing to select a representative who best suits the interests of the district, and then the elected representatives decide how to select the mayor of Beijing. Of course, we hope that the representatives elected by each district can best meet the interests of that district. To make a simple analogy with pooling, Beijing 〈-〉 input matrix; Chaoyang District, Haidian District and other 〈-〉 local areas; each district represents the 〈-〉 output matrix (if they sit according to geographical location during a meeting, this is the same as the characteristics of pooling Very similar).
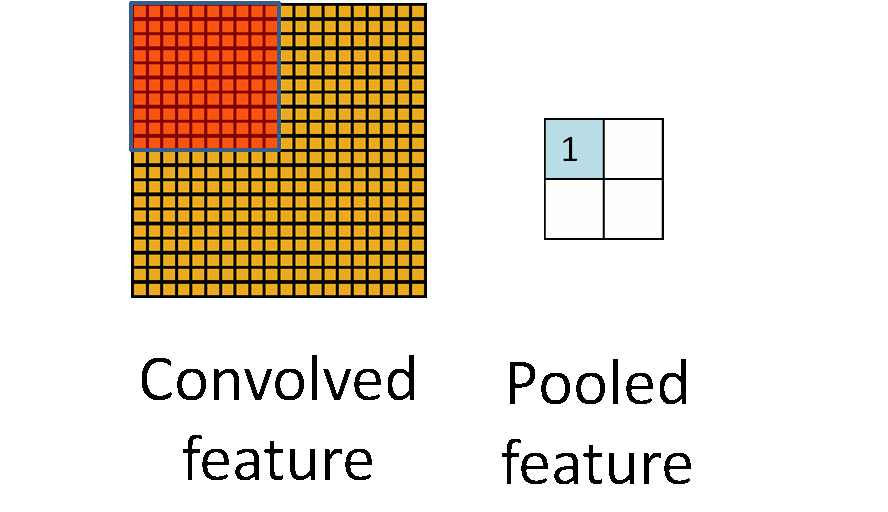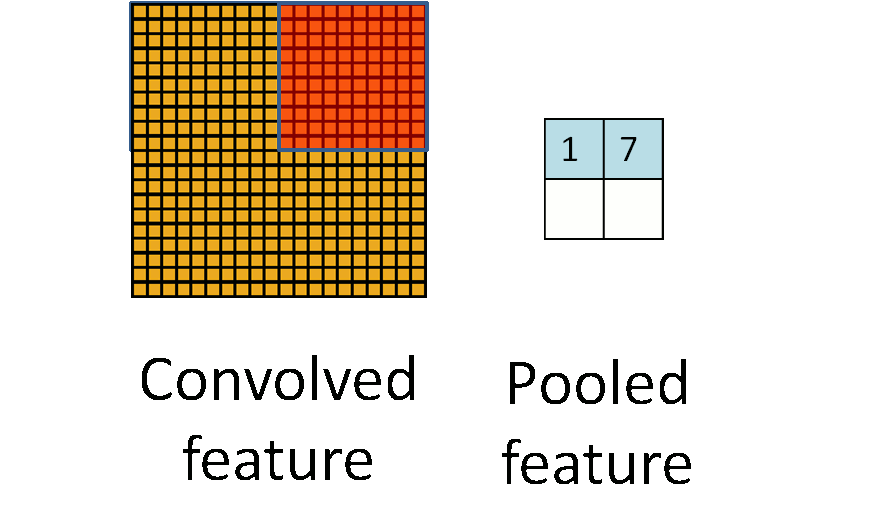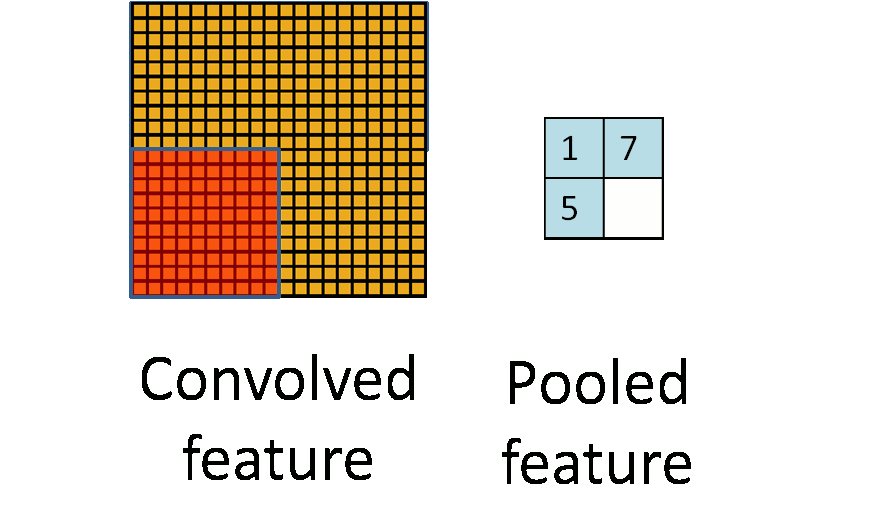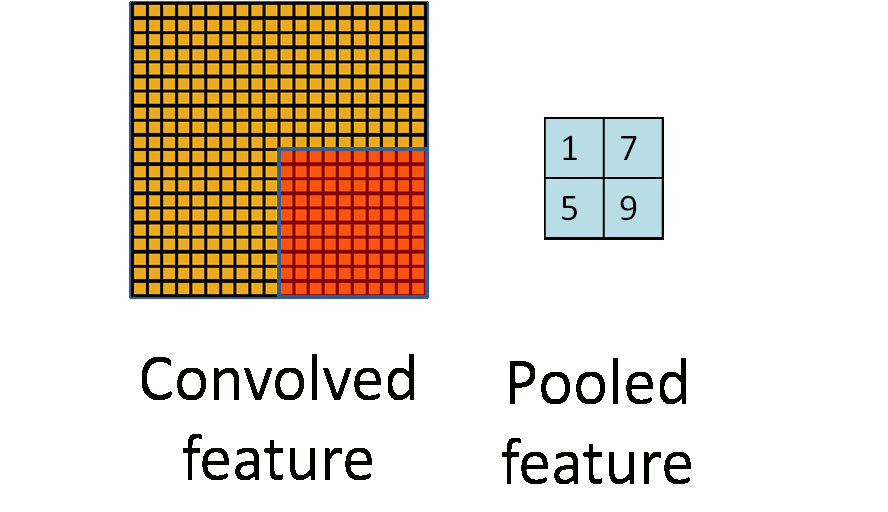
2. The reason behind pooling
In the process of selecting representatives in a local area, our general approach is to select the most prestigious person in the area as the representative (corresponding to max pooling) or select the person who best represents the area. People with general characteristics of the area owners are used as representatives (corresponding to mean pooling). Correspondingly, there are two common methods in pooling: the one with the largest local area value wins as the representative of the area or all the values in the area are taken. average as representative of the area.
Choose the most reputable person in the area as a representative vs. select the person who best represents the general characteristics of everyone in the area as a representative. The advantages are:
1) The most reputable person in a local area is not suitable when electing the mayor. There is a deviation, but he may rely on his old age and cannot represent the views of the general public in the area (local maximum values, it is easy to ignore the general characteristics of the area)
2) Although the person who best represents the general characteristics of everyone in the area can represent the The greatest rights and interests of all residents in the region, but due to his limited cognitive ability (the local mean is small, so his cognitive ability is limited), bias is prone to occur when selecting the mayor.
3) If the people in the area have a certain degree of freedom of movement (corresponding to translation and rotation invariance), it will basically have no impact on the above two methods of selecting representatives.
Formal explanation of pooling
According to relevant theories: (1) The variance of the estimated value increases due to the limited size of the neighborhood; (2) The error causes the deviation of the estimated mean. Generally speaking, mean-pooling can reduce the first error and retain more background information of the image, while max-pooling can reduce the second error and retain more texture information.
Generally, the input dimension of pooling is high and the output dimension is low. This can be understood as dimensionality reduction to a certain extent. Based on the above explanation of the pooling principle, we can infer that this dimensionality reduction process greatly retains Some of the most important information to enter. In the actual application of pooling, we need to conduct a detailed analysis based on the characteristics of the actual problem. In fact, once you know the operation and principle of pooling, if it is well combined with specific problems, it will be a good innovation point, haha.
3. Python implementation of pooing
Some of the author’s thoughts when writing the code are as follows. The core is to split a complex problem into a problem that can be directly implemented with code:
1) The input matrix can be mxn, It can also be mxnxp. If you directly consider these two forms when writing code, you will not know where to start (there are a lot of situations to consider, and I am easily confused by multi-dimensional matrices). After careful analysis, I found that if I implement the pooling of the mxn matrix, then the mxnxp matrix can be easily implemented using the implementation of the mxn matrix.
2) For mxn matrix input, it is possible that the orange box in Figure 1 cannot exactly cover the input matrix, so the input matrix needs to be expanded. The expansion is also very simple. As long as the poolSize corresponding to the last poolStride can cover the input matrix, the others can definitely be covered.
3) Finally, the for loop performs similar operations.
def pooling(inputMap,poolSize=3,poolStride=2,mode='max'):
"""INPUTS:
inputMap - input array of the pooling layer
poolSize - X-size(equivalent to Y-size) of receptive field
poolStride - the stride size between successive pooling squares
OUTPUTS:
outputMap - output array of the pooling layer
Padding mode - 'edge'
"""
# inputMap sizes
in_row,in_col = np.shape(inputMap)
# outputMap sizes
out_row,out_col = int(np.floor(in_row/poolStride)),int(np.floor(in_col/poolStride))
row_remainder,col_remainder = np.mod(in_row,poolStride),np.mod(in_col,poolStride)
if row_remainder != 0:
out_row +=1
if col_remainder != 0:
out_col +=1
outputMap = np.zeros((out_row,out_col))
# padding
temp_map = np.lib.pad(inputMap, ((0,poolSize-row_remainder),(0,poolSize-col_remainder)), 'edge')
# max pooling
for r_idx in range(0,out_row):
for c_idx in range(0,out_col):
startX = c_idx * poolStride
startY = r_idx * poolStride
poolField = temp_map[startY:startY + poolSize, startX:startX + poolSize]
poolOut = np.max(poolField)
outputMap[r_idx,c_idx] = poolOut
# retrun outputMap
return outputMap
# 测试实例
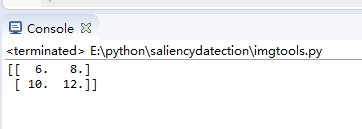
test = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
test_result = pooling(test, 2, 2, 'max')
print(test_result)Test results:
Summary: First understand the input, output and functions of a technology; then look for similar examples in life; finally, break down the technology into achievable steps.




