Big O Notations

It is a notation that determines how fast or slow an algorithm is running. This speed is not determined by seconds, but by how much the running time of an algorithm increases as the elements increase.

Big O is the relationship between time and size. Throughout the article you'll see graphs with these measures and you'll understand them better in practice. We have two types of complexity (spatial and temporal).

Temporal Complexity: Determines how long it will take to execute the algorithm proportional to the size of the input.

Spatial Complexity: Determines how much memory will be allocated to find the item we need.

Why study this?

• With this you can determine how scalable an algorithm is
• Big O always deals with the worst case, example below:

example:

• You have a list and you want to search for an item but the item is at the end of the list. The worst case scenario is that you have to perform as many operations as possible until you find the data you want.

Execution times

Tempo Constante O(1):

• regardless of the size of the array, it will always take the same amount of time

example:

• Increment or decrement

function increment(value: number){
  return ++value
}

function decrement(value: number){
  return --value
}

• Take a specific item

const fruits = ["apple", "orange", "grape", "banana"]

function getItem(items: string[], index: number) {
  return items[index]
}

const item = getItem(fruits, 2)
console.log(`fruit: ${item}`) // "grape"

• Get the first element of an array

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getFirstElement(items: string[]){
 return items[0]
}

• Get the last item in an array

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getLastElement(items: string[]){
 return items[item.length - 1]
}

let lastElement = getLastElement(animes)
console.log(`Last Element: ${lastElement}`)

Linear Time O(n):

• Execution time grows proportional to the size of the array
• Sorting and binary search algorithm
• iteration using only one loop

examples:

• To find the largest number in an array of 10 items, I will scroll through all the items until I find it.
• In the worst case, the largest number will be the last one.

const numbers = [0, 4, 8, 2, 37, 11, 7, 48]

function getMaxValue(items: number[]) {
    let max = numbers[0];
    for (let i=0; i <= items.length; i++){
      if(items[i] > max) {
        max = items[i]
      }
    }

    return max;
}

let maxValue = getMaxValue(numbers)

console.log(`Max Value: ${maxValue}`)

Logarithmic Time O(log n)

• Input size increases by n and execution time increases by log n, time grows in logarithmic proportion.
• Remember that n is the number of elements in the array.
• Input grows faster than execution time.

example:

• we will perform a binary search in an array to find a specific item.

const numbers = [0, 9, 24, 78, 54, 88, 92, 100, 21, 90]

function binarySearch(nums: number[], target: number) {
    let left = 0;
    let right = nums.length - 1;

    while (left <= right) {
        let middle = Math.floor((right + left) / 2);

        if (nums[middle] === target) {
            return middle;
        } else if (nums[middle] < target) {
            left = middle + 1;
        } else {
            right = middle - 1;
        }
    }

    return -1;
}

let getTarget = binarySearch(numbers, 92)
console.log(`Target: ${getTarget}`)

• To better understand logarithmic growth, let's look at it as follows: the array we're using in the example has 10 inputs, so:

log2(10) = 3.4
log2(20) = 4.3
log2(40) = 5.3

• The graph below will make it easier to understand:

Linearithmic/quasilinear time O(n log n)

• Time complexity of an algorithm that refers to the execution of logarithmic operations n times.
• A mixture of O(log(n)) and O(n).
• An example of a structure is the Merge Sort.
• grows moderately.

• One part scales in n and the other part scales in log(n), the example below is a lucky merge:

function increment(value: number){
  return ++value
}

function decrement(value: number){
  return --value
}

Quadratic Time O(n²)

• Execution time increases quadratically as the number of inputs increases.
• Reading matrix.
• Basically when 2 nested loops are required
• Bubble Sort

example:

const fruits = ["apple", "orange", "grape", "banana"]

function getItem(items: string[], index: number) {
  return items[index]
}

const item = getItem(fruits, 2)
console.log(`fruit: ${item}`) // "grape"

Time Exponential O(2ˆn)

• With each element inserted into the input, the execution time will double.

• an example of this code is fibonacci

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getFirstElement(items: string[]){
 return items[0]
}

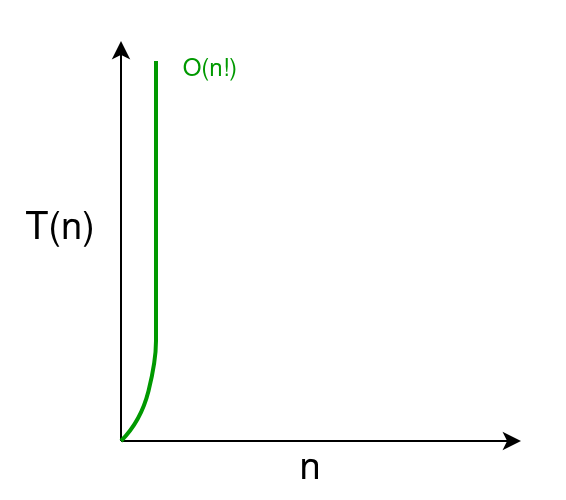
Factorial Time O(n!)

• Execution time increases factorially according to the size of the input.

example:

• Generate all permutations within an array

const animes = ["one piece", "dragon ball", "naruto", "demon slayer"]

function getLastElement(items: string[]){
 return items[item.length - 1]
}

let lastElement = getLastElement(animes)
console.log(`Last Element: ${lastElement}`)

The above is the detailed content of Big O Notations. For more information, please follow other related articles on the PHP Chinese website!