Understanding merge sort algorithm: Beginner&#s guide to mastering sorting algorithm

In our previous articles, we've learned about quite a number of sorting algorithms like Bubble Sort, Selection Sort as well as Insertion Sort. We've learned that while these sorting algorithms are very easy to implement, they are not efficient for large datasets, which means we need a more efficient algorithm to handle sorting large datasets, hence merge sort. In this series, we'll go through how merge sort works and how it can be implemented in JavaScript. You ready?

Table of Contents

1. What is Merge Sort Algorithm?
2. How Merge Sort Algorithms Works
   • Time Complexity
   • Space Complexity
3. Implementation in JavaScript
4. Conclusion

What is Merge Sort Algorithm?

Merge Sort Algorithm is an excellent sorting algorithm that follows the divide-and-conquer principle. Unlike simpler algorithms like Selection Sort and Bubble Sort that make multiple passes through the array comparing adjacent elements, Merge Sort takes a more strategic approach:

1. Divide: firstly, merge sort split the array into two halves
2. Conquer: secondly, it recursively sort each half
3. Combine: lastly, it merges the sorted halves back together

This approach consistently outperforms simpler O(n²) algorithms like Selection Sort and Bubble Sort when dealing with larger datasets.

How Merge Sort Algorithms Works

We've seen that merge sort works by using the popular divide-and-conquer approach. Below is a visual representation of how it works.

Now that we'v seen the magic, let's walk through how merge sort algorithm works by manually sorting this array: [38, 27, 43, 3, 9, 82, 10] using the approach mentioned above.

Step 1: Dividing

The first step in merge sort is dividing the array into subarrays, and then dividing each subarray into subarrays, and the subarray into subarrays until we have just one item left in all the subarrays.

Step 2: Merging Back (Conquering)

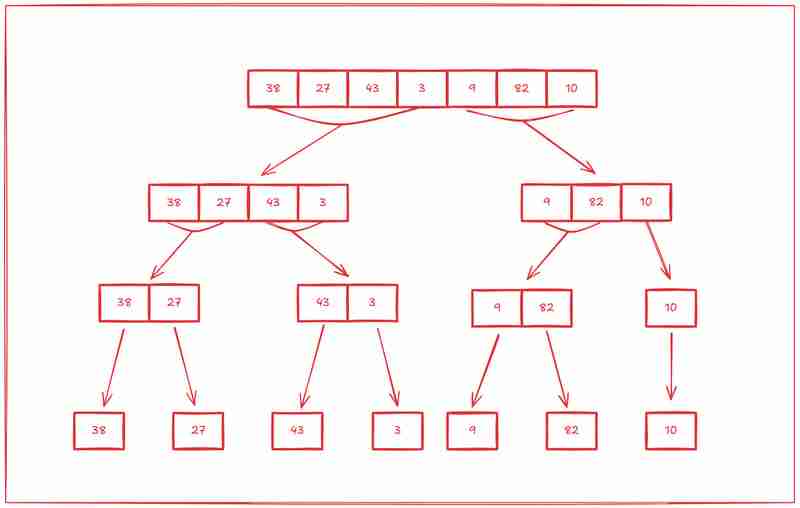
The second step is to start sorting those subarrays from the ground up.

Time Complexity

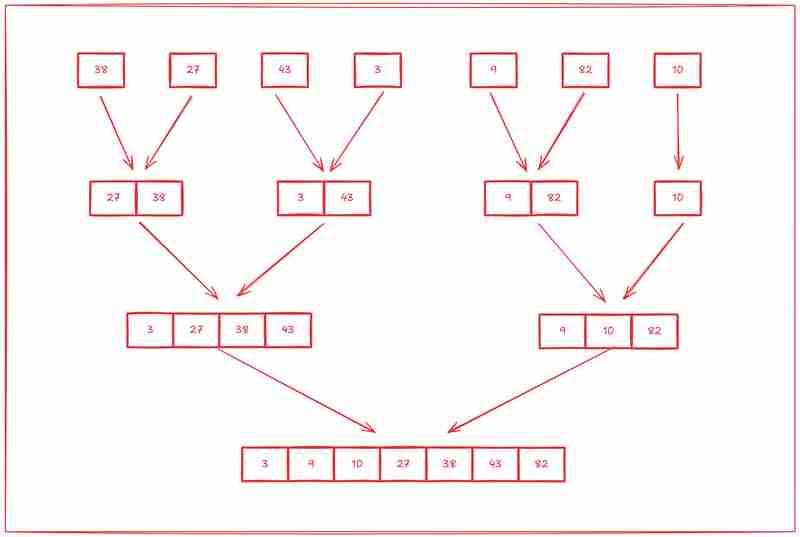
Merge Sort achieves O(n log n) time complexity in all cases (best, average, and worst), making it more efficient than O(n²) algorithms for larger datasets.

Here's why:

• Dividing: The array is divided log n times (each division cuts the size in half)
• Merging: Each level of merging requires n operations
• Total: n operations × log n levels = O(n log n)

Compare this to:

• Bubble Sort: O(n²)
• Selection Sort: O(n²)
• Merge Sort: O(n log n)

For an array of 1,000 elements:

• O(n²) ≈ 1,000,000 operations
• O(n log n) ≈ 10,000 operations

Space Complexity

Merge Sort requires O(n) additional space to store the temporary arrays during merging. While this is more than the O(1) space needed by Bubble Sort or Selection Sort, the time efficiency usually makes this trade-off worthwhile in practice.

Implementation in JavaScript

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

Breaking Down the Merge Function:

1. Function Setup:

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

• Creates an empty array to store merged results
• Initializes pointers for both input arrays
• Think of these pointers like fingers keeping track of where we are in each array

1. Main Merging Logic:

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

• Compares elements from both arrays
• Takes the smaller element and adds it to result
• Moves the pointer forward in the array we took from
• Like choosing the smaller of two cards when sorting a deck

1. Cleanup Phase:

   while (leftIndex < left.length) {
     result.push(left[leftIndex]);
     leftIndex++;
   }

• Adds any remaining elements
• Necessary because one array might be longer than the other
• Like gathering the remaining cards after comparing

The Main Merge Sort Function

function mergeSort(arr) {
  // Base case
  if (arr.length <= 1) {
    return arr;
  }

  // Divide
  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  // Conquer and Combine
  return merge(mergeSort(left), mergeSort(right));
}

Breaking Down MergeSort:

1. Base Case:

   if (arr.length <= 1) {
     return arr;
   }

• Handles arrays of length 0 or 1
• These are already sorted by definition
• Acts as our recursion stopping point

1. Division Phase:

   const middle = Math.floor(arr.length / 2);
   const left = arr.slice(0, middle);
   const right = arr.slice(middle);

• Splits array into two halves
• slice() creates new arrays without modifying original
• Like cutting a deck of cards in half

1. Recursive Sorting and Merging:

   return merge(mergeSort(left), mergeSort(right));

• Recursively sorts each half
• Combines sorted halves using merge function
• Like sorting smaller piles of cards before combining them

Example Walkthrough

Let's see how it sorts [38, 27, 43, 3]:

1. First Split:

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

1. Second Split:

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

1. Merge Back:

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

Conclusion

Merge Sort stands out as a highly efficient sorting algorithm that consistently performs well on large datasets. While it requires additional space compared to simpler sorting algorithms, its O(n log n) time complexity makes it a go-to choice for many real-world applications where performance is crucial.

Key takeaways:

• Uses divide-and-conquer strategy
• O(n log n) time complexity in all cases
• Requires O(n) additional space
• Stable sorting algorithm
• Excellent for large datasets

Stay Updated and Connected

To ensure you don't miss any part of this series and to connect with me for more in-depth
discussions on Software Development (Web, Server, Mobile or Scraping / Automation), data
structures and algorithms, and other exciting tech topics, follow me on:

Emmanuel Ayinde Follow

Software Engineer | Technical Writer | Backend, Web & Mobile Developer ? | Passionate about crafting efficient and scalable software solutions. #letsconnect ?

• GitHub
• Linkedin
• X (Twitter)

Stay tuned and happy coding ?‍??

The above is the detailed content of Understanding merge sort algorithm: Beginner&#s guide to mastering sorting algorithm. For more information, please follow other related articles on the PHP Chinese website!