
2807. Insert Greatest Common Divisors in Linked List
Difficulty: Medium
Topics: Linked List, Math, Number Theory
Given the head of a linked list head, in which each node contains an integer value.
Between every pair of adjacent nodes, insert a new node with a value equal to the greatest common divisor of them.
Return the linked list after insertion.
The greatest common divisor of two numbers is the largest positive integer that evenly divides both numbers.
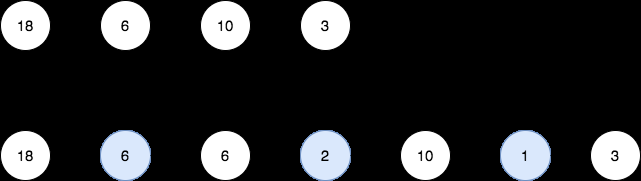
Example 1:
Example 2:

Example 3:
Constraints:
Hint:
Solution:
We need to insert nodes between every pair of adjacent nodes in a linked list. The value of the inserted node should be the greatest common divisor (GCD) of the two adjacent nodes' values. We'll traverse the linked list, calculate the GCD for every pair of adjacent nodes, and then insert the new node accordingly.
Here's how you can approach this:
Let's implement this solution in PHP: 2807. Insert Greatest Common Divisors in Linked List
<?php
// Definition for a singly-linked list node.
class ListNode {
public $val = 0;
public $next = null;
public function __construct($val = 0, $next = null) {
$this->val = $val;
$this->next = $next;
}
}
/**
* Function to calculate the GCD of two numbers.
*
* @param $a
* @param $b
* @return mixed
*/
function gcd($a, $b) {
...
...
...
/**
* go to ./solution.php
*/
}
/**
* @param ListNode $head
* @return ListNode
*/
function insertGreatestCommonDivisors($head) {
...
...
...
/**
* go to ./solution.php
*/
}
/**
* Function to print the linked list for testing purposes.
*
* @param $head
* @return void
*/
function printList($head) {
$current = $head;
while ($current != null) {
echo $current->val . " ";
$current = $current->next;
}
echo "\n";
}
// Example usage:
// Create the linked list: 18 -> 6 -> 10 -> 3
$head = new ListNode(18);
$head->next = new ListNode(6);
$head->next->next = new ListNode(10);
$head->next->next->next = new ListNode(3);
// Insert GCD nodes.
$modifiedHead = insertGreatestCommonDivisors($head);
// Print the modified linked list.
printList($modifiedHead);
// Output should be: 18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3
?>
<h3>
Explanation:
</h3>
<ol>
<li><p><strong>ListNode Class</strong>: This class represents the structure of a node in the linked list, with properties for the value ($val) and the next node ($next).</p></li>
<li><p><strong>GCD Calculation</strong>: The gcd function uses the Euclidean algorithm to compute the greatest common divisor of two integers.</p></li>
<li>
<p><strong>Main Logic (insertGreatestCommonDivisors)</strong>:</p>
<ul>
<li>We loop through the linked list until we reach the second-to-last node.</li>
<li>For each pair of adjacent nodes, we compute the GCD of their values.</li>
<li>We create a new node with this GCD value and insert it between the current node and the next node.</li>
</ul>
</li>
<li><p><strong>Edge Case</strong>: If the list has only one node, we return it as is without making any changes since there are no adjacent nodes.</p></li>
<li><p><strong>Testing</strong>: The function printList is a helper function used to output the values of the linked list for verification.</p></li>
</ol>
<h3>
Time Complexity:
</h3>
<ul>
<li>The time complexity of this solution is (O(n)), where (n) is the number of nodes in the linked list. Calculating the GCD for each adjacent pair takes constant time on average, and we perform a linear traversal of the list.</li>
</ul>
<h3>
Example:
</h3>
<p>For the input list [18, 6, 10, 3], the output is:<br>
</p>
<pre class="brush:php;toolbar:false">18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!
If you want more helpful content like this, feel free to follow me:
The above is the detailed content of Insert Greatest Common Divisors in Linked List. For more information, please follow other related articles on the PHP Chinese website!
 How to use the month function
How to use the month function
 The difference between master and host
The difference between master and host
 Wireless network card cannot connect
Wireless network card cannot connect
 How to export pictures to pdf
How to export pictures to pdf
 Windows 10 running opening location introduction
Windows 10 running opening location introduction
 What does nohup mean?
What does nohup mean?
 How to open an account with u currency
How to open an account with u currency
 How to copy an Excel table to make it the same size as the original
How to copy an Excel table to make it the same size as the original




