Case Study: Computing Factorials

A recursive method is one that invokes itself. Many mathematical functions are defined using recursion. Let’s begin with a simple example. The factorial of a number n can be recursively defined as follows:

0! = 1;
n! = n × (n - 1)!; n > 0

How do you find n! for a given n? To find 1! is easy, because you know that 0! is 1, and 1! is 1 × 0!. Assuming that you know (n - 1)!, you can obtain n! immediately by using n × (n - 1)!. Thus, the problem of computing n! is reduced to computing (n - 1)!. When computing (n - 1)!, you can apply the same idea recursively until n is reduced to 0.

Let factorial(n) be the method for computing n!. If you call the method with n = 0, it immediately returns the result. The method knows how to solve the simplest case, which is referred to as the base case or the stopping condition. If you call the method with n > 0, it reduces the problem into a subproblem for computing the factorial of n - 1. The subproblem is essentially the same as the original problem, but it is simpler or smaller. Because the subproblem has the same property as the original problem, you can call the method with a different argument, which is referred to as a recursive call.

The recursive algorithm for computing factorial(n) can be simply described as follows:

if (n == 0)
return 1;
else
return n * factorial(n - 1);

A recursive call can result in many more recursive calls, because the method keeps on dividing a subproblem into new subproblems. For a recursive method to terminate, the problem must eventually be reduced to a stopping case, at which point the method returns a result to its caller. The caller then performs a computation and returns the result to its own caller. This process continues until the result is passed back to the original caller. The original problem can now be solved by multiplying n by the result of factorial(n - 1).

The code below gives a complete program that prompts the user to enter a nonnegative integer and displays the factorial for the number.

The factorial method (lines 17–22) is essentially a direct translation of the recursive mathematical definition for the factorial into Java code. The call to factorial is recursive because it calls itself. The parameter passed to factorial is decremented until it reaches the base case of 0.

You see how to write a recursive method. How does recursion work behind the scenes? Figure below illustrates the execution of the recursive calls, starting with n = 4.

The use of stack space for recursive calls is shown in Figure below.

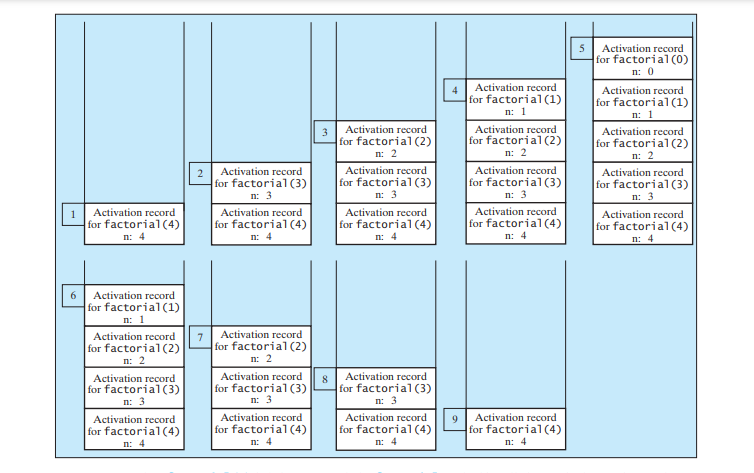
It is simpler and more efficient to implement the factorial method using a loop. However, we use the recursive factorial method here to demonstrate the concept of recursion. Later in this chapter, we will present some problems that are inherently recursive and are difficult to solve without using recursion.

If recursion does not reduce the problem in a manner that allows it to eventually converge into the base case or a base case is not specified, infinite recursion can occur. For example, suppose you mistakenly write the factorial method as follows:

public static long factorial(int n) {
return n * factorial(n - 1);
}

The method runs infinitely and causes a StackOverflowError.

The example discussed in this section shows a recursive method that invokes itself. This is known as direct recursion. It is also possible to create indirect recursion. This occurs when method A invokes method B, which in turn invokes method A. There can even be several more methods involved in the recursion. For example, method A invokes method B, which invokes method C, which invokes method A.

The above is the detailed content of Case Study: Computing Factorials. For more information, please follow other related articles on the PHP Chinese website!