【PaddlePaddle】基础理论教程 - 前馈神经网络概论-人工智能-PHP中文网

本文介绍前馈神经网络（FNN），其源于对生物神经网络的研究，可追溯至20世纪40年代。文中阐述了其发展背景，详解结构设计，包括输入层、隐藏层、输出层及层间连接，还介绍了数据构成、神经元运算原理，分析多种激活函数特性，并展示了简单前馈神经网络的构建过程与计算示例。

【paddlepaddle】基础理论教程 - 前馈神经网络概论 - php中文网

一、前馈神经网络的发展背景介绍

前馈神经网络（Feedforward Neural Network，FNN）起源于对生物神经网络的研究，是人工智能发展的早期成果之一。其概念最早可以追溯到20世纪40年代，神经科学家沃伦·麦卡洛克（Warren McCulloch）和数学家沃尔特·皮茨（Walter Pitts）提出的麦卡洛克-皮茨神经元模型。这一模型为神经网络的数学基础奠定了重要基石。

1958年，心理学家弗兰克·罗森布拉特（Frank Rosenblatt）设计了感知机（Perceptron），这是前馈神经网络的早期形式之一，也是第一个硬件实现的人工神经网络。虽然感知机只能处理线性可分问题，但它标志着人工智能研究的正式开启。

在80年代，受保罗·韦尔斯（Paul Werbos）提出的误差反向传播算法（Backpropagation）的推动，前馈神经网络进入了蓬勃发展的阶段。该算法解决了训练深层神经网络的主要难题，使得网络可以通过调整权重更精确地拟合复杂的数据模式。

随着计算能力的提升和大数据的涌现，前馈神经网络逐渐成为现代深度学习的基础。它的简洁性和可扩展性使其在诸多领域奠定了应用基础，同时也为卷积神经网络（CNN）和循环神经网络（RNN）等更复杂的架构提供了理论支持。

前馈神经网络是人工神经网络中最基础和广泛使用的一种结构。它模仿了生物神经网络的信息处理方式，由多个相互连接的神经元组成，信息在网络中以单向流动的方式从输入层传递到输出层。前馈神经网络的核心优势在于其强大的非线性建模能力，能够通过隐藏层和激活函数对复杂的非线性关系进行逼近和学习。作为深度学习的基础，前馈神经网络广泛应用于分类、回归、图像识别、自然语言处理等领域，是深入学习其他复杂模型的必备知识点。

二、前馈神经网络结构设计

前馈神经网络（Feedforward Neural Network, FNN）是由多个层组成的神经网络，其中的每一层都由若干神经元构成。网络的设计通常包括输入层、隐藏层和输出层。在这部分中，我们将专注于前馈神经网络的层级结构设计，逐一介绍各层的作用、神经元的配置以及层与层之间的关系。

2.1 输入层（Input Layer）

输入层是神经网络的第一层，主要功能是接收外部输入的数据。每个输入神经元对应于一个特征，因此输入层的神经元数量等于输入数据的特征数。输入层的神经元不会进行任何计算，它们只是将数据传递到下一层。

例如，在处理图像数据时，输入层的每个神经元对应于图像的一个像素；在处理表格数据时，输入层的每个神经元对应于一个特征。

2.2 隐藏层（Hidden Layers）

隐藏层位于输入层和输出层之间，是神经网络的核心部分。隐藏层的神经元负责从输入中提取特征，并通过激活函数对加权和进行非线性变换。隐藏层的层数和每层的神经元数目对于神经网络的学习能力和计算复杂度有着重要影响。

层数选择：隐藏层的层数决定了网络的深度，通常情况下，更多的隐藏层可以让网络捕捉到更复杂的特征。深层神经网络可以学习更为抽象的特征表示，但也容易导致过拟合。
神经元数量：每个隐藏层的神经元数目影响网络的表达能力。神经元过少可能导致网络的表现不佳（欠拟合），而神经元过多则可能导致计算开销过大和过拟合。

在设计隐藏层时，可以根据问题的复杂性调整层数和神经元数目。在实际应用中，通常会采用层数较少、神经元数目适中的设计来平衡性能和计算效率。

输出层（Output Layer）

输出层是神经网络的最后一层，它负责将神经网络的计算结果转化为实际输出。输出层的神经元数目与具体任务密切相关：

分类任务：如果任务是多分类问题，则输出层的神经元数目等于类别的数量，每个神经元表示一个类别的概率。对于二分类问题，通常只使用一个神经元，通过激活函数（如Sigmoid）输出概率。
回归任务：如果任务是回归问题，则输出层通常只有一个神经元，表示预测的连续值。

输出层通常使用激活函数（例如，Softmax用于多分类任务，Sigmoid用于二分类任务）来将神经网络的输出转化为适合任务需求的格式。

2.4 层与层之间的连接

在前馈神经网络中，层与层之间的连接是全连接的。即每一层的每个神经元都与上一层的所有神经元相连，并且每一连接都有一个权重。这些权重决定了神经元之间的信号传递强度，并在训练过程中通过梯度下降法进行优化。

权重矩阵：每一层的输出依赖于上一层的输出与当前层的权重。假设上一层的输出为 $a^{(l - 1)}$ a(l−1)，当前层的权重为 $W^{(l)}$ W(l)，偏置为 $b^{(l)}$ b(l)，则当前层的输入为：

$z^{(l)} = W^{(l)} a^{(l - 1)} + b^{(l)}$ z(l)=W(l)a(l−1)+b(l)

经过激活函数后，当前层的输出为：

$a^{(l)} = f (z^{(l)})$ a(l)=f(z(l))

其中， $f$ f 是激活函数，通常使用非线性函数（如ReLU、Sigmoid、Tanh等）。

2.5 网络层级设计示意图

前馈神经网络的层级结构可以用以下简化的图示表示：

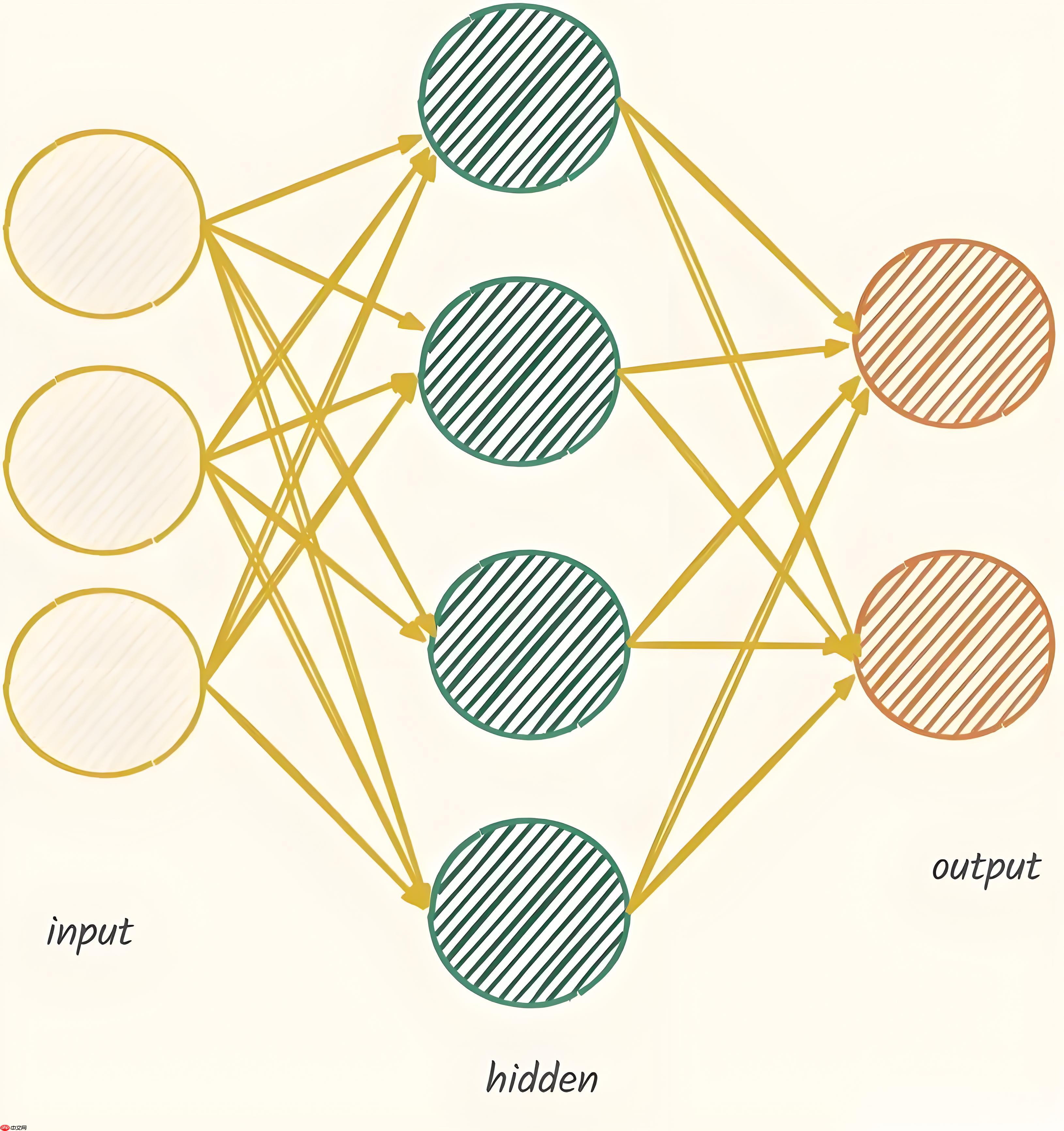
【PaddlePaddle】基础理论教程 - 前馈神经网络概论 - php中文网

在这个简化的示意图中：

输入层（x1, x2, x3）代表输入数据的特征。
隐藏层由若干神经元组成。
输出层（y1, y2, y3）生成最终的预测结果。

三、前馈神经网络的基本单元、数据构成与基本运算原理

前馈神经网络（Feedforward Neural Network, FNN）是由多个层级的神经元组成的模型。

3.1 数据的构成

在前馈神经网络中，数据的基本构成是向量，每个数据点可以看作是一个具有多个特征的向量。假设我们有一个用于训练的输入数据集，通常输入数据集被表示为一个矩阵 X ，每一行代表一个数据样本，每一列代表一个特征。具体来说

$X = [\begin{matrix} x_{1} & x_{2} & \dots & x_{n} \end{matrix}]$ X=[x1x2…xn]

其中， $n$ n 是特征数目。每个输入特征 $x_{i}$ xi 都是网络学习的基础。通过将这些数据传递给网络，网络通过一系列的计算得到输出。

假设我们有一个样本 $x = [x_{1}, x_{2}, \dots, x_{n}]$ x=[x1,x2,…,xn] ，其中 $x_{1}, x_{2}, \dots, x_{n}$ x1,x2,…,xn 分别表示输入特征（例如：图像的像素值、表格数据的特征等）。

3.2 神经元的基本单元

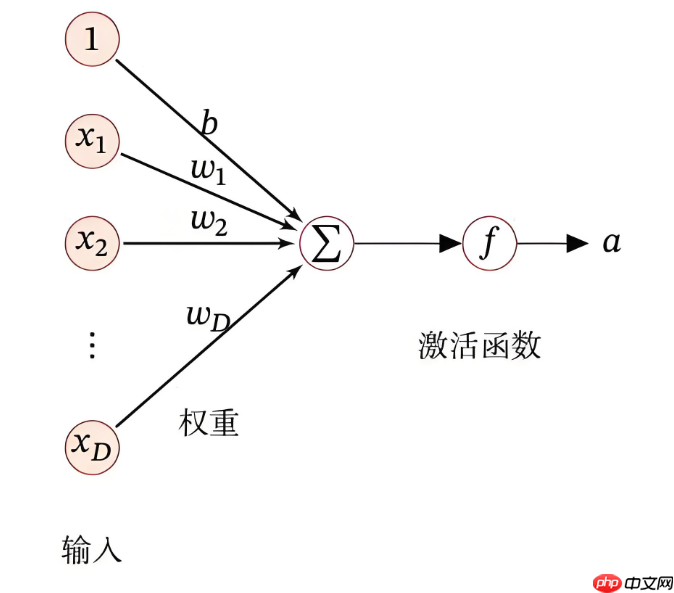
在前馈神经网络中，每个神经元（或称为节点）都做着相似的工作：接收输入数据、计算加权和、应用激活函数，最后输出结果。我们来看一下每个神经元的工作流程。

加权和：

神经元首先将来自上一层的输入值进行加权。假设上一层的输出为

$a^{(l - 1)} = [a_{1}^{(l - 1)}, a_{2}^{(l - 1)}, \dots, a_{m}^{(l - 1)}]$ a(l−1)=[a1(l−1),a2(l−1),…,am(l−1)] ，权重为 $W^{(l)}$ W(l) 和偏置为 $b^{(l)}$ b(l)

那么神经元的输入加权和（即线性变换）为：

$z^{(l)} = W^{(l)} \cdot a^{(l - 1)} + b^{(l)}$ z(l)=W(l)⋅a(l−1)+b(l)

其中：
- $W^{(l)}$ W(l) 是当前层的权重矩阵，表示上一层的神经元与当前层的神经元之间的连接强度。
- $b^{(l)}$ b(l) 是当前层的偏置项，用来调整输出值。
- $a^{(l - 1)}$ a(l−1) 是上一层的输出（可以是输入数据或上一层的结果）。
激活函数：

加权和 $z^{(l)}$ z(l) 经过一个激活函数进行非线性变换，得到当前神经元的输出 $a^{(l)}$ a(l) 。常用的激活函数包括：
- Sigmoid 激活函数：
  
  $σ (z) = \frac{1}{1 + e^{- z}}$ σ(z)=1+e−z1
该函数的输出范围是 $(0, 1)$ (0,1) ，常用于二分类问题。
- ReLU 激活函数（Rectified Linear Unit）：
  
  $ReLU (z) = \max (0, z)$ ReLU(z)=max(0,z)
该函数会将负数变为零，常用于隐藏层。
- Tanh 激活函数：
  
  $t a n h (z) = \frac{e^{z} - e^{- z}}{e^{z} + e^{- z}}$ tanh(z)=ez+e−zez−e−z
输出范围是 (-1, 1) ，常用于某些深度学习任务。激活函数的目的是引入非线性因素，使得神经网络能够逼近任何复杂的非线性映射。因此，神经元的最终输出是：

$a^{(l)} = f (z^{(l)}) = f (W^{(l)} \cdot a^{(l - 1)} + b^{(l)})$ a(l)=f(z(l))=f(W(l)⋅a(l−1)+b(l))

【PaddlePaddle】基础理论教程 - 前馈神经网络概论 - php中文网

3.3 各层间的连接与数据流

在前馈神经网络中，信息是通过层与层之间的连接传递的。每一层的神经元与上一层的神经元是完全连接的，这称为全连接（Fully Connected）。

假设我们有两层网络：输入层和隐藏层。输入层的输出是 $a^{(0)} = x$ a(0)=x ，经过第一层计算后，得到隐藏层的输出 $a^{(1)}$ a(1) 。然后，隐藏层的输出又将作为输入传递到下一层（如输出层）。

每一层的输出 $a^{(l)}$ a(l) 都是通过上一层的输出 $a^{(l - 1)}$ a(l−1) 加权和偏置计算得出的，接着通过激活函数得到。

3.4 示例：单一神经元的计算

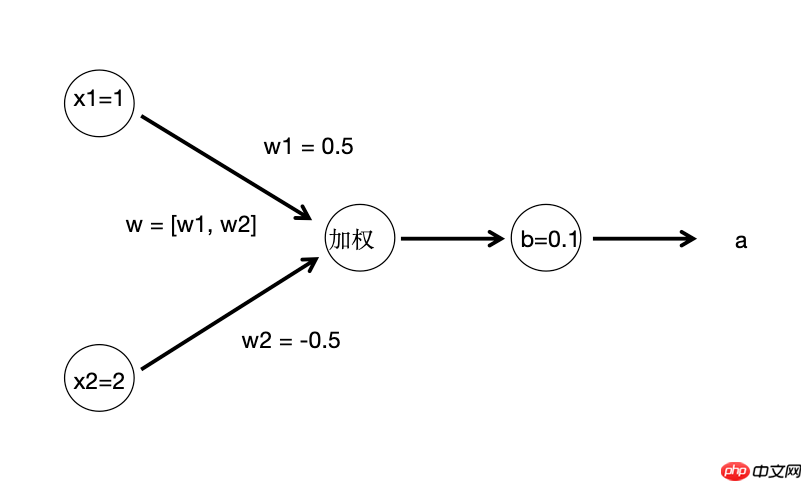
假设我们有一个简单的网络，其中输入层包含两个输入 $x_{1}$ x1 和 $x_{2}$ x2 ，并且隐藏层有一个神经元。

假设输入层的值是 $x_{1} = 1$ x1=1 和 $x_{2} = 2$ x2=2 ，权重矩阵 $W = [0.5, - 0.5]$ W=[0.5,−0.5] ，偏置项 $b = 0.1$ b=0.1 ，激活函数为ReLU。

（这个神经网络图包含了一个输入层，和一个隐藏层（只有一个神经元）。输入层有两个节点 x_1 和 x_2，它们分别与隐藏层的神经元连接。权重 $w_{1}$ w1 和 $w_{2}$ w2 分别作用于 x_1 和 x_2，并且有一个偏置项 b。）

计算加权和：

$z = 0.5 \cdot 1 + (- 0.5) \cdot 2 + 0.1 = 0.5 - 1.0 + 0.1 = - 0.4$ z=0.5⋅1+(−0.5)⋅2+0.1=0.5−1.0+0.1=−0.4

激活函数（ReLU）：

$a = ReLU (- 0.4) = \max (0, - 0.4) = 0$ a=ReLU(−0.4)=max(0,−0.4)=0

因此，经过这一层处理后，神经元的输出是 a = 0 。

【PaddlePaddle】基础理论教程 - 前馈神经网络概论 - php中文网

四、激活函数与特性详解

4.1 Sigmoid 激活函数

原理分析：

Sigmoid 函数是一个 S 形曲线函数，常用于二分类问题。它的输出值范围在 0 到 1 之间，通常用来表示概率。

数学公式：

$σ (x) = \frac{1}{1 + e^{- x}}$ σ(x)=1+e−x1

假设输入值 x = 1 ，计算 Sigmoid 激活函数：

$σ (1) = \frac{1}{1 + e^{- 1}} = \frac{1}{1 + 0.3679} = 0.731$ σ(1)=1+e−11=1+0.36791=0.731

特性与作用：

输出范围：0 到 1。
作用：用于输出概率值，通常应用于二分类问题。
特性：
- 输出值接近 0 或 1 时，梯度消失问题严重。
- 计算比较慢，特别是当输入值非常大或非常小时。

In [2]

# PaddlePaddle实现import paddleimport numpy as np# 输入数据x = paddle.to_tensor(np.array([1.0, 2.0, -1.0], dtype=np.float32))# 使用Paddle的Sigmoid激活函数sigmoid_output = paddle.nn.functional.sigmoid(x)print(sigmoid_output.numpy())

登录后复制

[0.7310586  0.880797   0.26894143]

登录后复制

In [3]

import numpy as npimport matplotlib.pyplot as plt# 创建输入数据x = np.linspace(-10, 10, 100)
y = 1 / (1 + np.exp(-x))# 绘制Sigmoid函数图plt.plot(x, y, label='Sigmoid Activation')
plt.title("Sigmoid Activation Function")
plt.xlabel("Input")
plt.ylabel("Output")
plt.grid(True)
plt.legend()
plt.show()

登录后复制

<Figure size 640x480 with 1 Axes>

登录后复制

4.2 ReLU 激活函数

原理分析：

ReLU（Rectified Linear Unit）是目前最常用的激活函数。它的特点是，对于正输入直接输出，对于负输入输出 0。

数学公式：

$ReLU (x) = \max (0, x)$ ReLU(x)=max(0,x)

计算案例：

假设输入值 x = -2 ，计算 ReLU 激活函数：

$ReLU (- 2) = \max (0, - 2) = 0$ ReLU(−2)=max(0,−2)=0

假设输入值 x = 3 ，计算 ReLU 激活函数：

$ReLU (3) = \max (0, 3) = 3$ ReLU(3)=max(0,3)=3

特性与作用：

输出范围：0 到正无穷。
作用：可以使网络更快地训练，适合深度神经网络。
特性：
- 计算非常简单且效率高。
- 负输入会被“截断”为 0，可能导致“死神经元”问题（即神经元永远不会激活）。

In [6]

# PaddlePaddle实现:import paddleimport numpy as np# 输入数据x = paddle.to_tensor(np.array([1.0, -2.0, 3.0], dtype=np.float32))# 使用Paddle的ReLU激活函数relu_output = paddle.nn.functional.relu(x)print(relu_output.numpy())

登录后复制

[1. 0. 3.]

登录后复制

In [7]

# 创建输入数据x = np.linspace(-10, 10, 100)
y = np.maximum(0, x)# 绘制ReLU函数图plt.plot(x, y, label='ReLU Activation')
plt.title("ReLU Activation Function")
plt.xlabel("Input")
plt.ylabel("Output")
plt.grid(True)
plt.legend()
plt.show()

登录后复制

<Figure size 640x480 with 1 Axes>

登录后复制

4.3 Tanh 激活函数

原理分析：

Tanh（双曲正切）函数与 Sigmoid 类似，但它的输出范围在 -1 到 1 之间，因此输出的结果对称于零，通常在回归问题中比较有用。

数学公式：

$\tanh (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$ tanh(x)=ex+e−xex−e−x

特性与作用：输出范围：-1 到 1。

作用：适合需要中心化的激活函数，通常用于隐藏层。
特性：
- 比 Sigmoid 更适用于深度网络，能更好地解决梯度消失问题。
- 计算比 Sigmoid 略慢。

In [8]

import paddleimport numpy as np# 输入数据x = paddle.to_tensor(np.array([1.0, -1.0, 0.5], dtype=np.float32))# 使用Paddle的Tanh激活函数tanh_output = paddle.nn.functional.tanh(x)print(tanh_output.numpy())

登录后复制

[ 0.7615942  -0.7615942   0.46211717]

登录后复制

In [9]

# 创建输入数据x = np.linspace(-10, 10, 100)
y = np.tanh(x)# 绘制Tanh函数图plt.plot(x, y, label='Tanh Activation')
plt.title("Tanh Activation Function")
plt.xlabel("Input")
plt.ylabel("Output")
plt.grid(True)
plt.legend()
plt.show()

登录后复制

<Figure size 640x480 with 1 Axes>

登录后复制

4.4 Leaky ReLU 激活函数

原理分析：

Leaky ReLU 是 ReLU 的一种变种，它解决了标准 ReLU 中“死神经元”的问题。当输入值为负时，它不会完全截断，而是以一个很小的斜率输出。

数学公式：

$LeakyReLU (x) = \max (α x, x)$ LeakyReLU(x)=max(αx,x)

其中 $α$ α 是一个小常数，通常取值为 0.01。

计算案例：

假设输入值 $x = - 2$ x=−2 且 $α = 0.01$ α=0.01 ，计算 Leaky ReLU 激活函数：

$LeakyReLU (- 2) = \max (0.01 \times (- 2), - 2) = - 0.02$ LeakyReLU(−2)=max(0.01×(−2),−2)=−0.02

假设输入值 x = 3 ，计算 Leaky ReLU 激活函数：

$LeakyReLU (3) = \max (0.01 \times 3, 3) = 3$ LeakyReLU(3)=max(0.01×3,3)=3

特性与作用：

输出范围：负数部分有斜率，正数部分与 ReLU 相同。
作用：解决 ReLU 的“死神经元”问题。
特性：
- 对于负输入，使用一个小的斜率代替 0，从而避免死神经元。
- 在训练深度网络时，能够提高效果和稳定性。

In [10]

# PaddlePaddle实现：import paddleimport numpy as np# 输入数据x = paddle.to_tensor(np.array([1.0, -2.0, 3.0], dtype=np.float32))# 使用Paddle的LeakyReLU激活函数leaky_relu_output = paddle.nn.functional.leaky_relu(x, negative_slope=0.01)print(leaky_relu_output.numpy())

登录后复制

[ 1.   -0.02  3.  ]

登录后复制

In [11]

# 创建输入数据x = np.linspace(-10, 10, 100)
y = np.maximum(0.01 * x, x)# 绘制Leaky ReLU函数图plt.plot(x, y, label='Leaky ReLU Activation')
plt.title("Leaky ReLU Activation Function")
plt.xlabel("Input")
plt.ylabel("Output")
plt.grid(True)
plt.legend()
plt.show()

登录后复制

<Figure size 640x480 with 1 Axes>

登录后复制

五、简单前馈神经网络的构建

这里将展示如何使用简单的输入数据构建一个前馈神经网络。这个网络将包含一个隐藏层和一个输出层。我们将使用ReLU作为隐藏层的激活函数，Sigmoid作为输出层的激活函数。

5.1 准备数据

我们将使用一个非常简单的例子来讲解前馈神经网络的结构。假设我们的输入数据只有两个特征

$X = [\begin{matrix} x_{1} & x_{2} & x_{3} & x_{4} \end{matrix}]$ X=[x1x2x3x4]

我们的目标是通过前馈神经网络来预测一个二分类结果（0或1），即输出 $y = output$ y=output 。

5.2 前馈神经网络的结构

输入层到隐藏层：对于输入数据 $x = [x_{1}, x_{2}]$ x=[x1,x2] ，我们需要计算每个隐藏层神经元的加权和，并通过激活函数处理。

加权和

$z^{(1)} k = w 1 k \cdot x_{1} + w_{2 k} \cdot x_{2} + b_{k}$ z(1)k=w1k⋅x1+w2k⋅x2+bk

其中， $w_{1 k}, w_{2 k}$ w1k,w2k 是输入到第 k 个隐藏层神经元的权重， b_k 是偏置。

ReLU 激活函数

$a_{k}^{(1)} = ReLU (z_{k}^{(1)}) = \max (0, z_{k}^{(1)})$ ak(1)=ReLU(zk(1))=max(0,zk(1))

5.2 隐藏层到输出层

隐藏层输出 $a^{(1)} = [a_{1}^{(1)}, a_{2}^{(1)}]$ a(1)=[a1(1),a2(1)] 传递到输出层，输出层计算加权和并通过 Sigmoid 激活函数产生输出：

加权和

$z^{(2)} out = w 11 \cdot a^{(1)} 1 + w 12 \cdot a^{(1)} 2 + b out$ z(2)out=w11⋅a(1)1+w12⋅a(1)2+bout

Sigmoid 激活函数

$a_{out} = σ (z^{(2)} out) = \frac{1}{1 + e^{- z^{(2)} out}}$ aout=σ(z(2)out)=1+e−z(2)out1

5.3 利用 PaddlePaddle 构建前馈神经网络

In [18]

# PaddlePaddle实现二维简单示例：import paddleimport numpy as np# 创建输入数据x_data = np.array([[0.5, 0.3]], dtype=np.float32)  # 两个输入特征# 定义前馈神经网络模型class SimpleFFNN(paddle.nn.Layer):
    def __init__(self):
        super(SimpleFFNN, self).__init__()
        self.fc1 = paddle.nn.Linear(in_features=2, out_features=2)  # 输入到隐藏层
        self.fc2 = paddle.nn.Linear(in_features=2, out_features=1)  # 隐藏层到输出层
        self.relu = paddle.nn.ReLU()  # ReLU 激活函数
        self.sigmoid = paddle.nn.Sigmoid()  # Sigmoid 激活函数
    
    def forward(self, x):
        x = self.fc1(x)  # 输入层到隐藏层
        x = self.relu(x)  # 隐藏层激活
        x = self.fc2(x)  # 隐藏层到输出层
        x = self.sigmoid(x)  # 输出层激活
        return x# 实例化模型model = SimpleFFNN()# 将数据转换为Paddle张量x = paddle.to_tensor(x_data)# 前向传播output = model(x)print("模型输出：", output.numpy())  # 输出模型预测结果

登录后复制

模型输出： [[0.38744217]]

登录后复制

In [42]

# PaddlePaddle实现多维示例：import paddleimport matplotlib.pyplot as pltimport numpy as np# 输入数据X = np.array([1, 2, 3, 4]).astype('float32')# 隐藏层权重和偏置W_h = np.array([[0.1, 0.2, 0.3, 0.4],
                [0.5, 0.6, 0.7, 0.8],
                [0.9, 1.0, 1.1, 1.2]]).astype('float32')
b_h = np.array([0.1, 0.2, 0.3]).astype('float32')# 输出层权重和偏置W_o = np.array([0.2, 0.3, 0.4]).astype('float32')
b_o = np.array([0.5]).astype('float32')# 计算隐藏层加权和z_h = np.dot(W_h, X) + b_h
a_h = np.maximum(0, z_h)  # ReLU激活函数# 计算输出层加权和z_o = np.dot(W_o, a_h) + b_oprint("输出结果：", z_o)# 使用Paddle框架定义前馈神经网络class SimpleNN(paddle.nn.Layer):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = paddle.nn.Linear(4, 3)  # 输入4维，输出3维
        self.fc2 = paddle.nn.Linear(3, 1)  # 输入3维，输出1维

    def forward(self, x):
        x = paddle.nn.functional.relu(self.fc1(x))  # ReLU激活
        x = self.fc2(x)        return x# 创建模型并进行预测model = SimpleNN()
input_data = paddle.to_tensor([1.0, 2.0, 3.0, 4.0])  # 输入数据output = model(input_data)print(f"通过Paddle框架输出：{output.numpy()}")# 可视化激活函数x_vals = np.linspace(-10, 10, 100)
y_vals = np.maximum(0, x_vals)  # ReLUplt.plot(x_vals, y_vals)
plt.title('ReLU Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.grid(True)
plt.show()

登录后复制

输出结果： [7.8]
通过Paddle框架输出：[6.3703694]

登录后复制

<Figure size 640x480 with 1 Axes>

登录后复制

5.4 模型推导和数学公式

计算隐藏层的加权和：假设我们有以下输入和权重矩阵：

$X = [\begin{matrix} x_{1} & x_{2} & x_{3} & x_{4} \end{matrix}] = [\begin{matrix} 1 & 2 & 3 & 4 \end{matrix}]$ X=[x1x2x3x4]=[1234]

隐藏层的权重矩阵：

$W_{h} = [\begin{matrix} 0.1 & 0.2 & 0.3 & 0.4 \\ 0.5 & 0.6 & 0.7 & 0.8 \\ 0.9 & 1.0 & 1.1 & 1.2 \end{matrix}]$ Wh=⎣⎢⎡0.10.50.90.20.61.00.30.71.10.40.81.2⎦⎥⎤

偏置：

$b_{h} = [\begin{matrix} 0.1 & 0.2 & 0.3 \end{matrix}]$ bh=[0.10.20.3]

计算隐藏层的加权和

$z_{h} = W_{h} \cdot X + b_{h} = [\begin{matrix} 0.1 \cdot 1 + 0.2 \cdot 2 + 0.3 \cdot 3 + 0.4 \cdot 4 \\ 0.5 \cdot 1 + 0.6 \cdot 2 + 0.7 \cdot 3 + 0.8 \cdot 4 \\ 0.9 \cdot 1 + 1.0 \cdot 2 + 1.1 \cdot 3 + 1.2 \cdot 4 \end{matrix}] + [\begin{matrix} 0.1 \\ 0.2 \\ 0.3 \end{matrix}]$ zh=Wh⋅X+bh=⎣⎢⎡0.1⋅1+0.2⋅2+0.3⋅3+0.4⋅40.5⋅1+0.6⋅2+0.7⋅3+0.8⋅40.9⋅1+1.0⋅2+1.1⋅3+1.2⋅4⎦⎥⎤+⎣⎢⎡0.10.20.3⎦⎥⎤

$z_{h} = [\begin{matrix} 3.0 & 5.0 & 7.0 \end{matrix}]$ zh=[3.05.07.0]

应用 ReLU 激活函数：

$a_{h} = ReLU (z_{h}) = [\begin{matrix} \max (0, 3.0) \\ \max (0, 5.0) \\ \max (0, 7.0) \end{matrix}] = [\begin{matrix} 3.0 & 5.0 & 7.0 \end{matrix}]$ ah=ReLU(zh)=⎣⎢⎡max(0,3.0)max(0,5.0)max(0,7.0)⎦⎥⎤=[3.05.07.0]