
Lean Copilot, dieses formale Mathematikwerkzeug, das von vielen Mathematikern wie Terence Tao gelobt wurde, hat sich erneut weiterentwickelt?
Soeben gab Caltech-Professorin Anima Anandkumar bekannt, dass das Team eine erweiterte Version des Lean Copilot-Papiers veröffentlicht und die Codebasis aktualisiert hat.
 Bilder
Bilder
Papieradresse: https://arxiv.org/pdf/2404.12534.pdf
Die neuesten Experimente zeigen, dass dieses Copilot-Tool mehr als 80 % der mathematischen Beweisschritte automatisieren kann! Dieser Rekord ist 2,3-mal besser als der vorherige Basiswert von Aesop.
Und wie bisher ist es Open Source unter der MIT-Lizenz.
 Bilder
Bilder
Er ist ein Chinese Song Peiyang. Er ist ehrenamtlicher CS-Student an der UCSB und SURF-Forscher in der Abteilung Computing + Mathematical Sciences (CMS) des California Institute of Technology.
Netizens riefen aus: Also kann Tao Zhexuans mathematische Forschung jetzt an Ort und Stelle um das Fünffache beschleunigt werden?
 Bilder
Bilder
Das Team veröffentlichte dieses Lean Copilot-Tool in der Hoffnung, eine Zusammenarbeit zwischen Menschen und LLM zu initiieren, um 100 % genaue formale mathematische Beweise zu schreiben.
Es löst eine zentrale technische Herausforderung: die Ausführung von LLM-Inferenz in Lean.
Mit diesem Tool können wir LLM Proof-Strategien in Lean vorschlagen lassen, sodass Menschen nahtlos eingreifen und Änderungen vornehmen können.
 Bilder
Bilder
Dieses Projekt wurde entwickelt, weil der automatisierte Theorembeweis auch heute noch eine schwierige Herausforderung darstellt.
Wir alle wissen, dass LLM bei Mathematik- und Denkaufgaben oft Fehler und Halluzinationen macht und sehr unzuverlässig ist.
 Bilder
Bilder
Mathematische Beweise wurden bislang meist manuell abgeleitet und bedürfen einer sorgfältigen Überprüfung.
Tools zum Beweisen von Theoremen wie Lean können jeden Schritt des Beweisprozesses formalisieren, aber es ist für Menschen sehr mühsam, Lean zu schreiben.
In diesem Fall ist die Geburt von Lean Copilot von großer Bedeutung.
LLM kann als Werkzeug verwendet werden, um Menschen beim Beweisen von Theoremen zu unterstützen. Dieses Argument wurde von Tao Zhexuan viele Male bestätigt.
Er hat gerade in seinem Blog vorhergesagt, dass KI in 26 Jahren mit Such- und symbolischen Mathematikwerkzeugen kombiniert werden und zu einem vertrauenswürdigen Co-Autor in der mathematischen Forschung werden wird.
Unmittelbar danach schossen Forschungsergebnisse, die seinen Standpunkt untermauerten, wie Pilze nach einem Regen aus dem Boden.
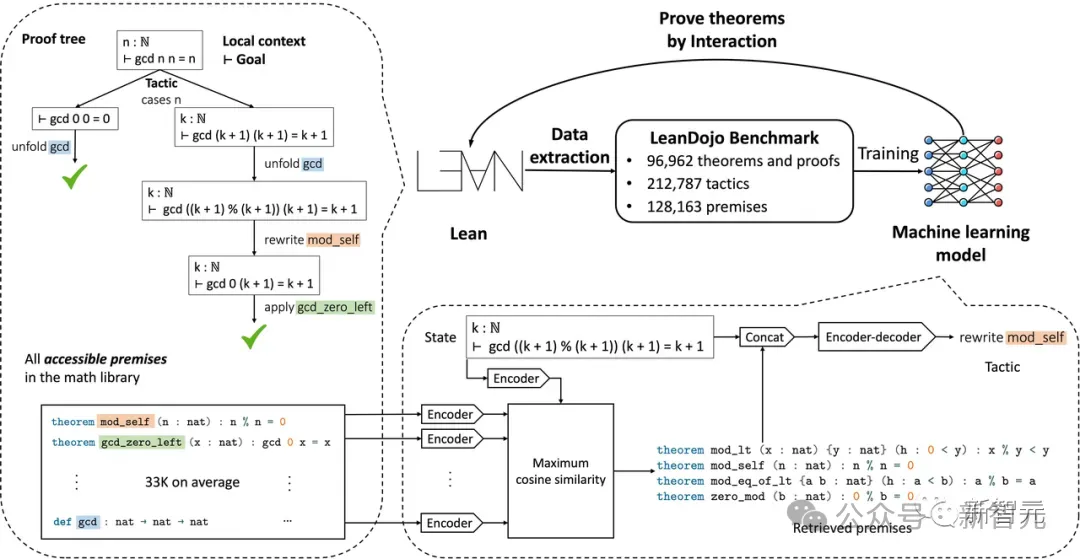
Im Juni letzten Jahres bauten Wissenschaftler des California Institute of Technology, NVIDIA, MIT und anderen Institutionen LeanDojo, einen Theorembeweis auf Basis von Open-Source-LLM.
 Bilder
Bilder
 Bilder
Bilder
In der 97. Dialogrunde kam GPT-4 zu dem Schluss, dass das Beispiel ohne die erschöpfende Methode nicht gelöst werden kann, was beweist, dass die Schlussfolgerung P≠NP ist
Im vergangenen Oktober Tao Zhexuan Mit Hilfe von GPT-4 und Copilot entdeckte er direkt einen versteckten Fehler in seiner Arbeit.
Bei der Verwendung von Lean4 zur Formalisierung des Arguments auf Seite 6 stellte er fest, dass der Ausdruck
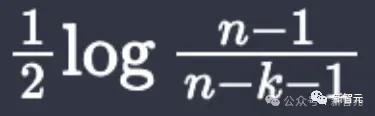 Bild
Bild
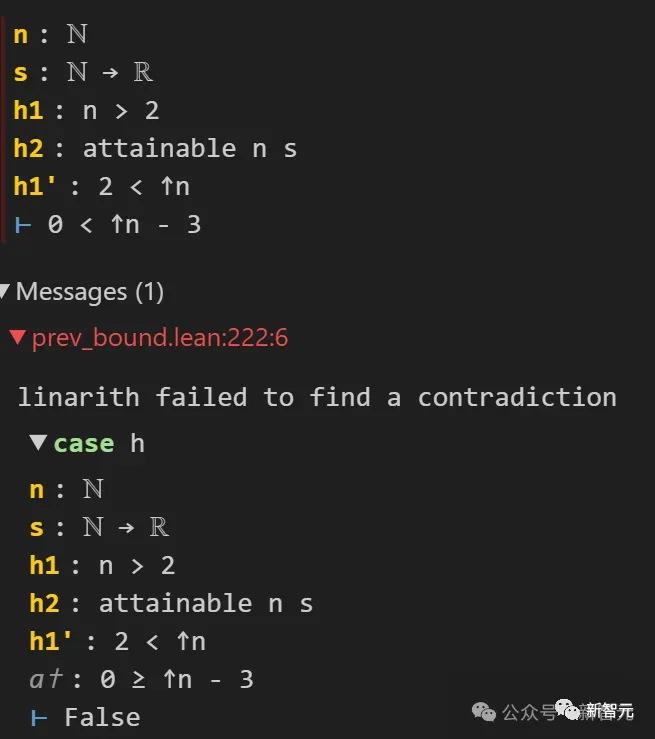
tatsächlich divergent ist, wenn n = 3, k = 2.
Dieser schwer erkennbare Fehler wurde dank Lean4 rechtzeitig erkannt. Der Grund dafür ist, dass Lean ihn gebeten hat, 0
 Bilder
Bilder
Diese Entdeckung schockierte die Schüler von Tao Zhexuan direkt.
 Bilder
Bilder
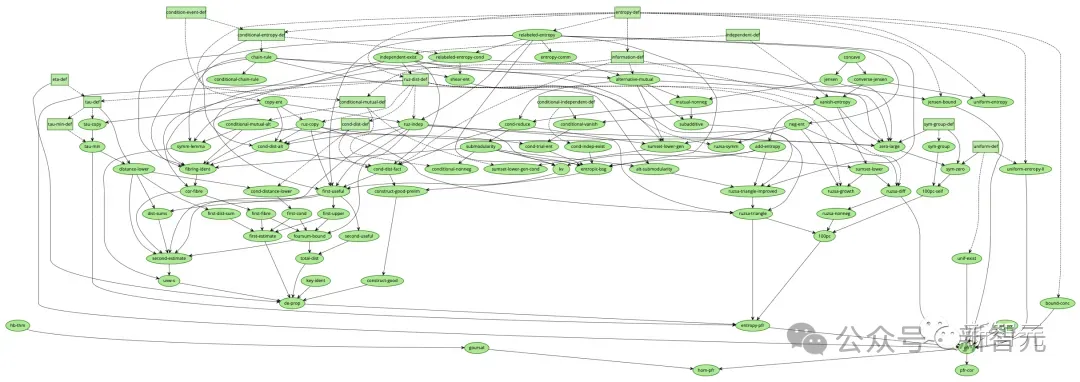
Ende letzten Jahres nutzte Tao Zhexuan direkt und erfolgreich KI-Tools, um die Arbeit zur Formalisierung des Polynom-Freiman-Ruzsa-Vermutungsbeweisprozesses abzuschließen.
 Bild
Bild
Schließlich wurde der Abhängigkeitsgraph vollständig mit Grün bedeckt, und der Lean-Compiler meldet auch, dass diese Vermutung vollständig den Standardaxiomen folgt.
 Bilder
Bilder
In diesem Prozess haben alle Mathematikforscher an vorderster Front zum ersten Mal den direkten Einfluss der KI auf die subversive Kraft der Mathematikforschung gespürt.
Und heute hat diese Forschung von Lean Copilot Lean direkt leistungsfähiger gemacht.
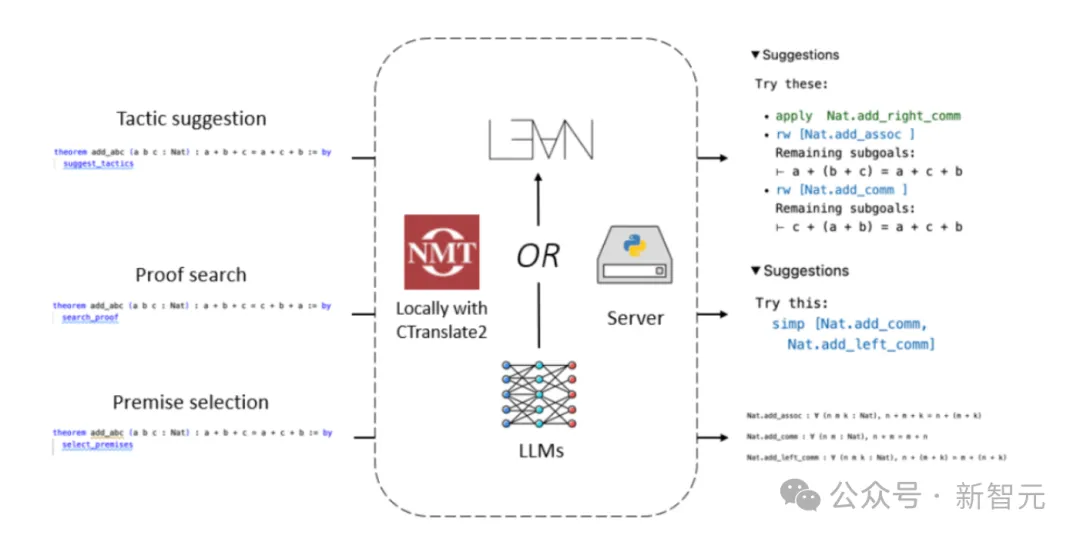
In diesem Artikel hat das Team auf Lean Copilot basierende Tools entwickelt, um Beweisschritte vorzuschlagen (Strategievorschlag), Zwischenziele für Beweise zu erreichen (Beweissuche) und relevante Prämissen mithilfe von LLM auszuwählen (Prämissenauswahl).
Die experimentellen Ergebnisse zeigen auch vollständig, dass Lean Copilot im Vergleich zur bestehenden regelbasierten Beweisautomatisierung in Lean Menschen effektiv beim automatisierten Theorembeweis unterstützt.
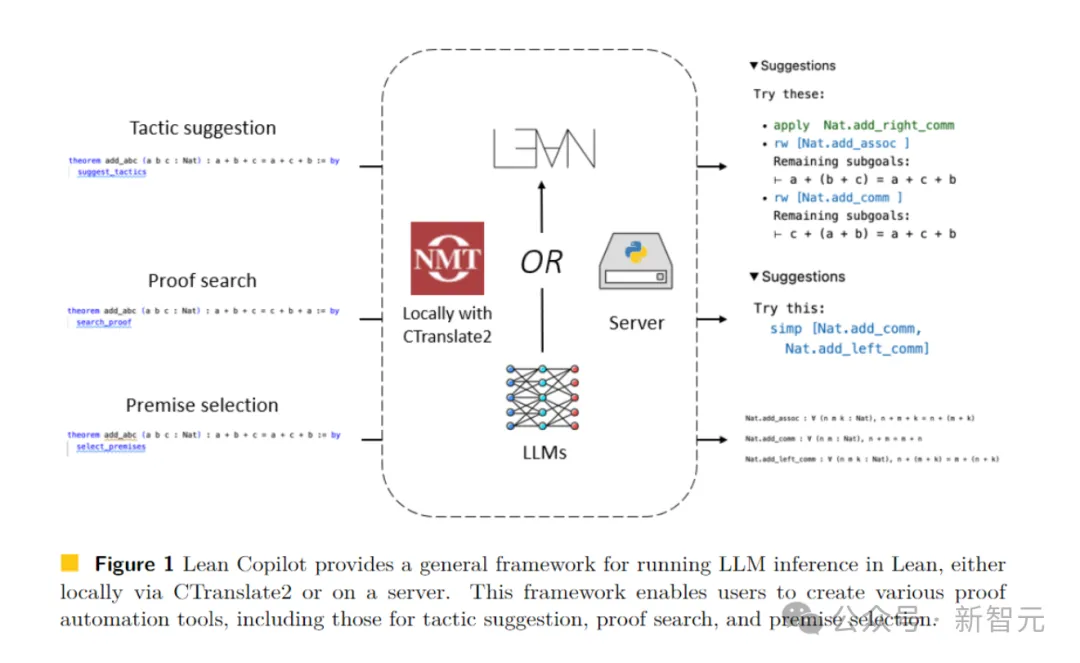
Lean Copilot bietet ein allgemeines Framework, das LLM-Inferenz lokal über CTranslate 2 oder auf dem Server ausführen kann.
Über dieses Framework können Benutzer verschiedene automatisierte Proof-Tools erstellen.
 Bilder
Bilder
Lean ist ein sehr beliebter Beweisassistent unter Mathematikern. Wie in der folgenden Abbildung dargestellt, besteht ein Beweis in Lean aus einer Reihe von Beweisschritten, die als Taktiken bezeichnet werden.
 Bilder
Bilder
Ausgehend vom Gesamtsatz als Ausgangsziel transformiert die Strategie das aktuelle Ziel iterativ in einfachere Unterziele, bis alle Ziele gelöst sind.
Benutzer schreiben interaktiv Strategien in der von VSCode gesteuerten IDE, und die Ziele werden im Infoansichtsbereich auf der rechten Seite angezeigt.
Mit Lean Copilot entwickelte das Team suggest_tropics, ein Tool zur Generierung von Strategievorschlägen mithilfe von LLM.
Und es selbst ist auch eine Strategie. Wenn
angewendet wird, gibt es das aktuelle Ziel in LLM ein und erhält die generierte Richtlinienkandidatenliste von LLM.
Bei jeder Option wird geprüft, ob sie 1) zu einem Fehler führt, 2) nichts Falsches ergibt, aber den Beweis nicht abschließen kann.
Wenn es 1 ist, wird diese Strategie gelöscht.
 Bilder
Bilder
Nur fehlerfreie Strategien werden im Ansichtsfeld rechts angezeigt.
Unter diesen sind Strategien, die den Beweis erfolgreich abschließen, mit Grün markiert (Kategorie 3); Strategien, die das Beweisziel ohne Fehler ändern, aber den Beweis nicht abschließen, sind mit Blau markiert (Kategorie 2).
Achtung! Wenn alle aufgeführten Strategien in Kategorie 2 fallen, können diese Informationen für den Benutzer äußerst wertvoll sein.
In diesem Fall können die Informationen der verbleibenden Ziele dem Benutzer direkt dabei helfen, eine Strategie als nächsten Zwischenbeweisschritt auszuwählen.
Nachdem Benutzer die Vorschläge gesehen haben, können sie entscheiden, ob sie diese annehmen oder sie als Inspirationsquelle für die Entwicklung neuer Strategien nutzen möchten.
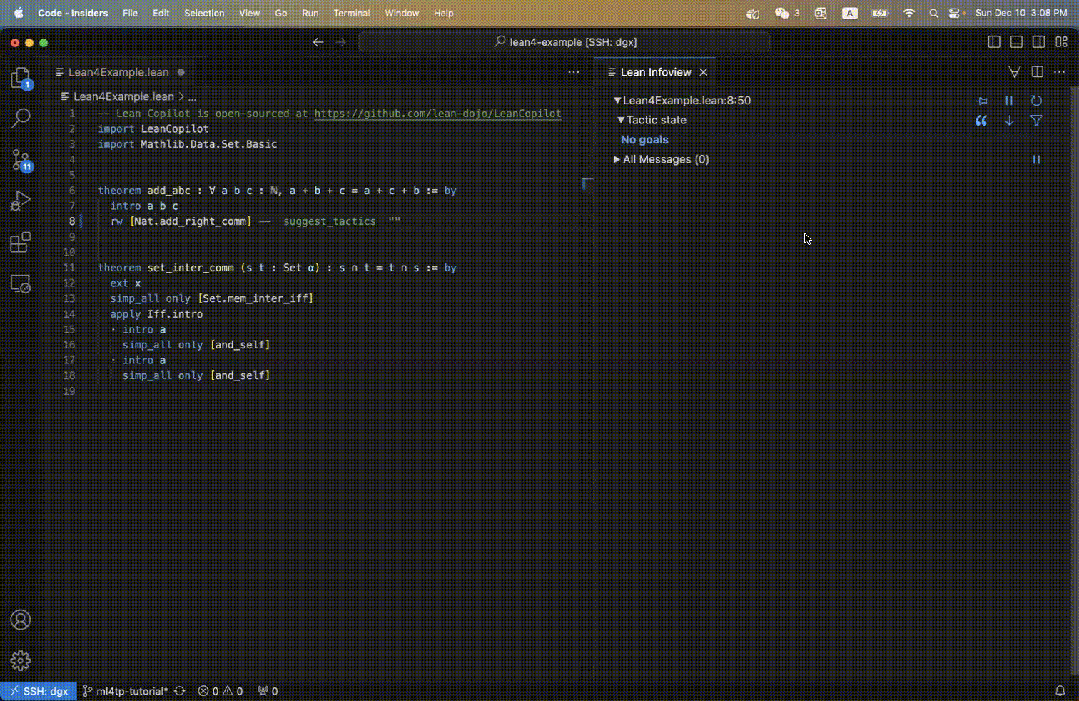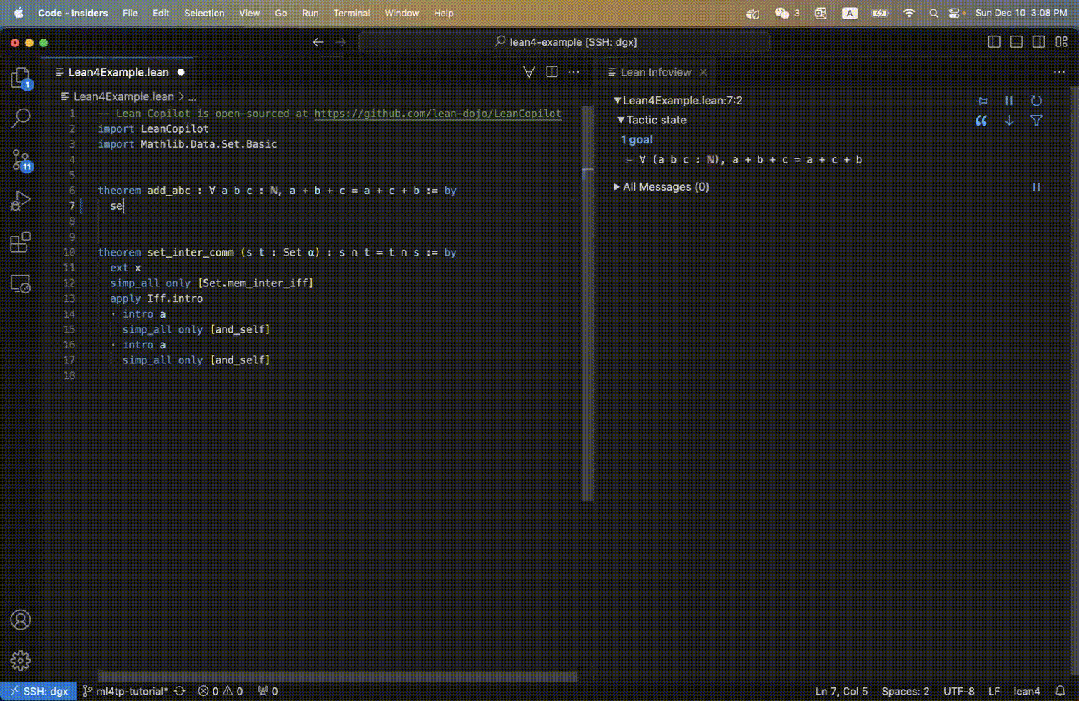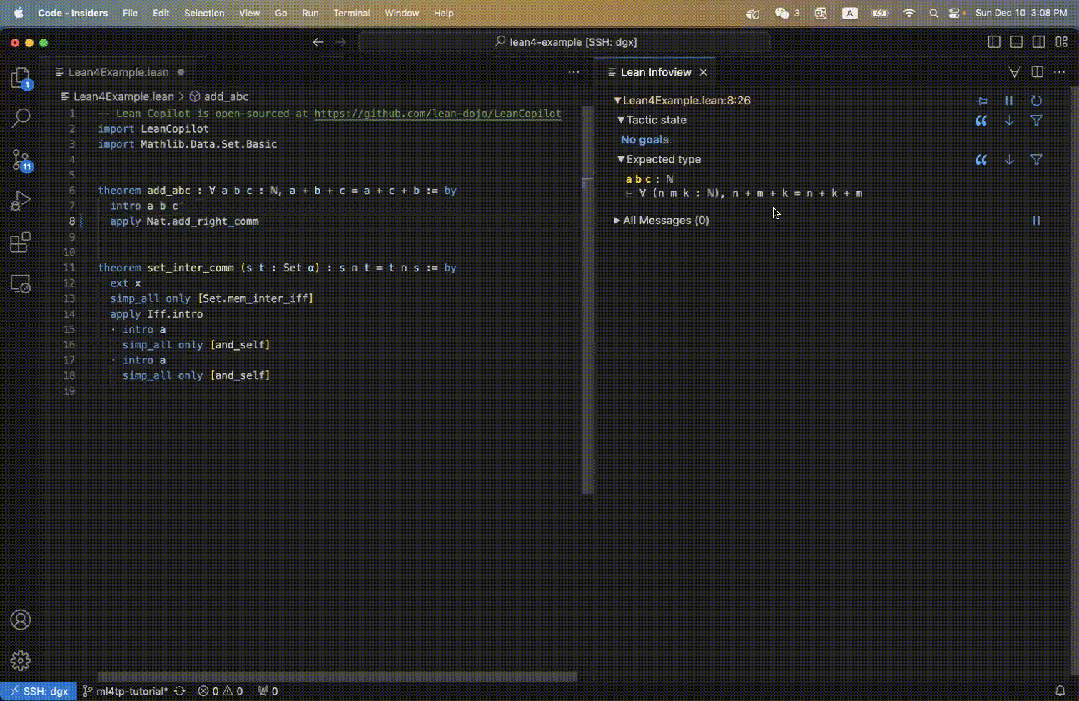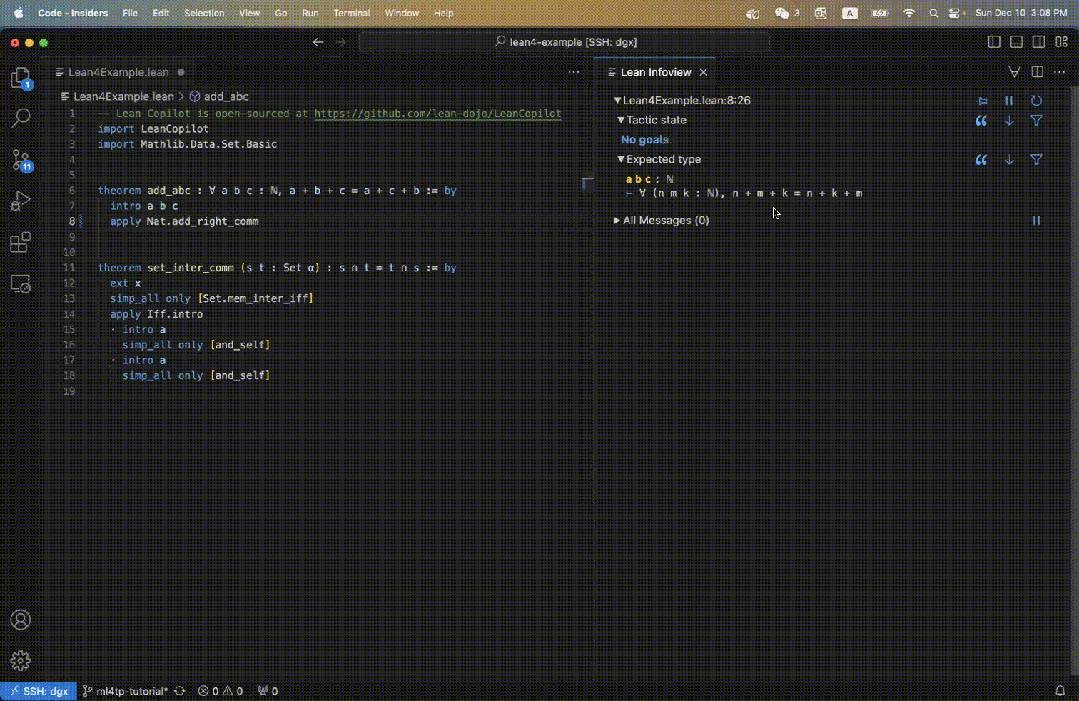
Zum Beispiel definieren wir im Lean-Code einen Satz add_abc, dessen ursprüngliches Ziel auf der rechten Seite von Abbildung 3 dargestellt ist.
 Bilder
Bilder
Wenn wir suggest_tropics eingeben, sehen wir rechts Strategievorschläge.
Die erste Strategie wird grün angezeigt, was darauf hinweist, dass der Beweis erfolgreich abgeschlossen wurde.
Die nächsten drei Vorschläge sind alle blau, was darauf hinweist, dass der Beweis nicht direkt abgeschlossen werden kann, aber nicht zu Fehlern führt.
Daher handelt es sich wahrscheinlich um gültige Zwischenbeweisschritte!
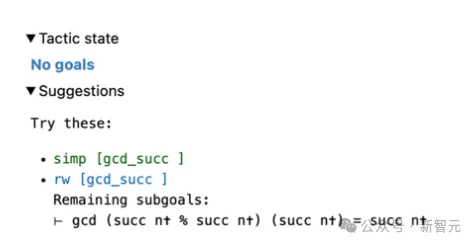
Gleichzeitig werden auch die restlichen Teilziele angezeigt.
Das Feld „Taktikstatus“ zeigt „Kein Ziel“, da mindestens ein Strategievorschlag nachgewiesen werden kann.
 Bilder
Bilder
Da außerdem weder Menschen noch Maschinen konsequent die richtige Strategie entwickeln können, muss der Prozess zurückgehen und verschiedene Alternativen erkunden, was die Beweissuche ist.
Wenn es um die oben erwähnten Suggest_tropics geht, kann es nur die Strategie des aktuellen Schritts generieren und verfügt nicht über die Möglichkeit, nach Beweisen für mehrere Strategien zu suchen.
Zu diesem Zweck kombinierte das Team es mit dem regelbasierten Proof-Suchtool aesop, um ein LLM-basiertes Proof-Suchtool zu erstellen.
Aesop wird die Best-First-Suche als Lean-Strategie implementieren und es Benutzern ermöglichen, zu konfigurieren, wie der Suchbaum erweitert wird.
 Bilder
Bilder
Der Suchbaum besteht aus Zielen als Knoten.
Zunächst hat es nur das ursprüngliche Ziel als Wurzelknoten. Bei jedem Schritt wählt Aesop den vielversprechendsten nicht erweiterten Knoten aus, erweitert ihn durch Anwendung einer Richtlinie und fügt den resultierenden Knoten als untergeordneten Knoten hinzu.
 Bilder
Bilder
Und wenn Aesop einen Weg von der Grundursache zu einem leicht lösbaren Ziel findet, beweist das, dass die Suche erfolgreich ist!
Daher hängt die Leistung von Aesop entscheidend davon ab, ob der Benutzer einen effektiven Regelsatz konfiguriert.
Das zeigt, dass es Aesop an Flexibilität mangelt. Daher erweitert Search_proof den Regelsatz von Aesop, indem er ihn mit zielbezogenen Richtlinien, die bei jedem Schritt von suggest_tropics generiert werden, flexibler macht.
Für das ursprüngliche Ziel in Abbildung 3 muss der Benutzer nur search_prrof eingeben und einen vollständigen Beweis finden, der das Ziel lösen kann, der in der Informationsansicht angezeigt wird (Abbildung 5 rechts).
Wie Sie sehen können, lautet der verbleibende Taktikstatus „Keine Ziele“, da Beweise für einen Erfolg gefunden wurden.
 Bilder
Bilder
Darüber hinaus besteht eine weitere herausfordernde und wichtige Aufgabe beim Theorembeweisen darin, relevante Prämissen zu finden, die den Beweis reduzieren oder vervollständigen.
Neben einer Vielzahl von Voraussetzungen in der Quellcode-Bibliothek und der Standardbibliothek verfügt Lean auch über eine große Mathematikbibliothek (Mathlib).
Allerdings ist die Suche nach geeigneten Räumlichkeiten in allen Bibliotheken äußerst schwierig und zeitaufwändig.
So viele Menschen versuchen, Unterstützung von Lean oder anderen Proof-Assistenten zu erhalten oder diesen Prozess zu automatisieren.
 Bilder
Bilder
In Lean ist die fortschrittlichste Methode zur Prämissenauswahl ein Framework, das auf Zufallswäldern (Random Forest) basiert und direkt in Lean implementiert wird.
Allerdings eignet sich die Prämissenauswahlaufgabe gut für abrufgestütztes LLM, bei dem die Abrufmatrix (Prämisseneinbettung) während des Trainings großer Modelle trainiert wird, um die Korrelation zwischen dem Beweisziel und den Kandidatenprämissen abzuschätzen.
Bei einem gegebenen Beweisziel zum Zeitpunkt der Inferenz kodieren Sie das Ziel zunächst in einen Vektor und führen dann eine Matrix-Vektor-Multiplikation zwischen der Prämisseneinbettung und dem Zielvektor durch.
Um dann die besten k Prämissen auszuwählen (wobei k ein Hyperparameter sein kann, der bestimmt, wie viele Prämissen der Benutzer zurückgeben möchte), geben Sie einfach die k Prämissen mit den höchsten Bewertungen zurück.
Um Argumentationsaufgaben in Lean auszuführen, benötigen Sie zusätzlich zu der schnellen Argumentation von Lean Copilot auch eine effiziente Matrixmultiplikationsbibliothek und einen C++-Numpy-Matrix-Reader.
Die Forscher verwendeten die Matrixmultiplikationsfunktion von CTranslate2 und den schnellen C++-Numpy-Dateireader von Libnpy.
Sie verknüpfen diese Zahlen über den FFI-Mechanismus erneut mit Lean.
Somit kann die Prämissenauswahlstrategie sehr effizient ablaufen, da die Prämisseneinbettungen vorberechnet werden können und alle nachfolgenden Operationen mithilfe der oben vorgestellten Bibliotheken schnell in C++ durchgeführt werden können.
Nachdem der Forscher die Prämisse der Rückkehr erhalten hatte, kommentierte er sie zusätzlich mit nützlichen Informationen.
Hier werden alle Räumlichkeiten in zwei Kategorien unterteilt: Räumlichkeiten, die direkt in der aktuellen Umgebung genutzt werden können (in-scope-Räumlichkeiten) und Räumlichkeiten, die nicht direkt in der aktuellen Umgebung genutzt werden können (out-of-scope-Räumlichkeiten).
Dies hängt davon ab, ob die benötigten Pakete importiert werden.
Sie können die Prämisse problemlos verwenden, wenn Sie die für die Prämisse erforderlichen Pakete bereits importiert haben. Abbildung 6 unten zeigt eine kommentierte Scope-Prämisse.

Abbildung 7 zeigt die kommentierte Out-of-Scope-Prämisse.

Das Folgende ist ein Beispiel für die Verwendung von „Prämissenauswahl“. Für den Satz add_abc in Abbildung 3 können Sie select_premises direkt in den Beweis eingeben (Abbildung 8 links).
Dann erscheint in der Informationsansicht eine Liste der zugehörigen Voraussetzungen (Abbildung 8, rechts).
Für diesen einfachen Satz ist deutlich zu erkennen, dass die gewählten Prämissen tatsächlich relevant sind, da sie alle mit natürlichen Zahlen und der Additionsregel zusammenhängen.
In diesem Fall befinden sich die 4 ausgewählten Räumlichkeiten alle im aktuellen Umfang, was bedeutet, dass ihre Module bereits importiert sind.

Die oben genannten sind drei praktische Tools zur Beweisautomatisierung, die von Forschern mit Lean Copilot entwickelt wurden und für Strategievorschläge, Suchbeweise und Prämissenauswahl verwendet werden.
Durch das Lean Copilot-Framework stellen Forscher empirisch die Hypothese auf, dass die Mensch-Maschine-Zusammenarbeit beim Lean Interactive Theorem Proving (ITP) von Vorteil ist.
Aufgrund des Theorembeweisprozesses in Lean liegt der Schwerpunkt hauptsächlich auf dem Strategiebeweis.
Daher hat der Autor im konkreten Experiment hauptsächlich die Proof-Automatisierungstools für „Strategievorschlag“ und „Proof-Suche“ evaluiert.
Zusammenfassend ist aesop derzeit das fortschrittlichste regelbasierte Proof-Automatisierungstool für die Proof-Suche.
Die Forscher überprüften die Wirksamkeit des LLM-basierten Suchbeweises im Vergleich zu Aesop in zwei Fällen:
(1) Autonomer Beweis des Theorems (LLM wurde unabhängig durchgeführt)
(2) Unterstützung beim Durchführen des Theorems durch Menschen Beweisen (Menschen und KI arbeiten zusammen)
Darüber hinaus verglichen die Forscher auch Suchbeweise mit Strategievorschlägen, um die Vorteile von Suchbeweisen zusätzlich zu einzelnen Strategievorschlägen zu beweisen.
Untersuchen Sie, wie Lean Copilot Menschen im ITP-Prozess effektiv helfen kann, ähnlich dem Paradigma, bei dem Menschen Copilot in der Softwareprogrammierung verwenden.
Das heißt, wenn wir vor einem Ziel stehen, rufen wir zuerst Copilot an, um zu sehen, ob es das Problem direkt lösen kann.
Wenn nicht, vereinfachen wir das Ziel weiter und versuchen es erneut mit Copilot. Anschließend wird der obige Vorgang wiederholt, bis Copilot die verbleibenden Ziele erfolgreich löst.
Die Forscher nutzten dieses Beispiel einer iterativen Zusammenarbeit, um zu sehen, wie viel Arbeitskraft jedes Proof-Automatisierungstool automatisieren kann.
Die spezifischen Ergebnisse sind in Tabelle 1 unten aufgeführt.
Die Beweissuche (search_proof) kann 64 % der Theoreme (32 von 50) automatisch beweisen, deutlich mehr als Aesop und Strategievorschläge (suggest_tropics).
Bei der Verwendung zur Unterstützung von Menschen erfordert die Beweissuche durchschnittlich nur 1,02 manuell eingegebene Strategien, was auch besser ist als Aesop (3,62) und Strategievorschläge (2,72).
 Bild
Bild
Abschließend berechneten die Autoren für jedes getestete Theorem den Prozentsatz der Beweisschritte, die von jedem der drei Tools automatisiert werden konnten.
Die Ergebnisse ergaben, dass die Beweissuche etwa 81,2 % der Beweisschritte im Theorem automatisch abschließen kann, was deutlich mehr ist als bei Strategievorschlägen (48,6 %) und Aesop (35,2 %).
Zusammenfassend ist die Leistung der Beweissuche 1,67-mal besser als die von Richtlinienvorschlägen und 2,31-mal besser als die des regelbasierten Basislinien-Aesop.
Taktikvorschlag, Beweissuche und Prämissenauswahl in Lean Copilot Diese drei Aufgaben sehen möglicherweise unterschiedlich aus, aber die Anforderungen an die Benutzererfahrung sind ähnlich.
Sie alle müssen schnell genug Antworten generieren, moderate Rechenanforderungen haben und gleichzeitig in Lean laufen.
Der Grund, warum Benutzer diese Anforderungen haben, liegt darin, dass Lean selbst in den meisten Fällen sehr schnell Umgebungsfeedback (wie verbleibende Ziele, Fehlermeldungen, Typinformationen usw.) bereitstellen kann.
Diese Geschwindigkeit steht im Einklang mit der Essenz des Beweissatzes – sie erfordert eine kohärente Argumentation.
Wenn Lean Copilot lange Wartezeiten der Benutzer erfordert, wird es schwierig, dass die Zusammenarbeit zwischen Mensch und KI funktioniert.
Gleichzeitig möchten wir auch den Anforderungen von Low Computing wirklich gerecht werden. Denn das Beweisen von Theoremen in Lean selbst erfordert keine GPU und kann auf dem lokalen Laptop des Benutzers ausgeführt werden.
Daher ist es für Lean-Benutzer sehr wichtig, dass sie auf der meisten Hardware (einschließlich Laptops ohne GPU) effizient laufen können.
Weil Benutzer beim Schreiben von Proofs möglicherweise keinen Zugriff auf CUDA-fähige GPUs haben.
Da schnelle Inferenz und geringe Rechenanforderungen erfüllt werden müssen und alle gängigen und effizienten Deep-Learning-Frameworks in Python sind, bestand eine natürliche Lösung, die sich das Team ausgedacht hat, darin, das Modell in Python (lokal oder remote) zu hosten Stellen Sie dann eine Anfrage an das Modell von Lean.
Dieser Ansatz leidet jedoch unter dem Overhead der prozessübergreifenden Kommunikation, erfordert von Benutzern die Durchführung zusätzlicher Einrichtungsschritte und ist für den traditionellen Lean-Workflow nicht geeignet.
Um diese Probleme zu lösen, führt Lean Copilot LLM nativ in Lean über das Foreign Function Interface (FFI) aus.
FFI ist ein Mechanismus, der es einem in einer Sprache geschriebenen Programm ermöglicht, ein Unterprogramm in einer anderen Sprache aufzurufen.
Der Lean-Teil ist in C++ implementiert und kann effizient mit C++ zusammenarbeiten.
Programmierer können eine Funktion in Lean deklarieren, den Funktionskörper jedoch in C++ implementieren. Die Implementierung wird in einer gemeinsam genutzten Bibliothek kompiliert und dynamisch mit Lean verknüpft.
Standardmäßig verwenden wir das vorab trainierte Repver-Modell von LeanDojo. Es basiert auf einem Encoder-Decoder-Konverter, BVT5, der Eingabestrings auf Ausgabestrings abbildet.
Lean Copilot macht es in Lean ausführbar, indem das Modell in eine C++-Funktion verpackt wird, die mit Strings arbeitet, die in Lean über FFI aufgerufen werden können.
 Bilder
Bilder
Das dreiköpfige Team im neuesten Artikel ist auch der Autor der Open-Source-Plattform LeanDojo vom 23. Juni.
 Bilder
Bilder
Papieradresse: https://arxiv.org/pdf/2306.15626.pdf
 Bilder
Bilder
Lied Peiyang studiert Informatik am College of Creative Studies (CCS) der UC Santa Barbara mit Auszeichnung und wird von Richert Wang und Phill Conrad betreut.
Gleichzeitig ist er auch SURF-Forscher im Department of Computational and Mathematical Sciences (CMS) am Caltech, gemeinsam betreut von Professor Anima Anandkumar und Dr. Kaiyu Yang.
 Bilder
Bilder
Darüber hinaus ist er Forscher am UC Berkeley Architecture Lab und arbeitet mit Tim Sherwood und Dr. Jeremy Lau (Google) zusammen.
Seine Forschungsinteressen sind maschinelles Lernen (ML) mit Anwendungsfeldern wie Natural Language Processing (NLP) und Computer Vision (CV) sowie grundlegende Theorien wie Systeme und Programmiersprachen (PL).
Song Peiyangs jüngste Forschung geht hauptsächlich in zwei Richtungen.
Eines ist Neural Symbolic Reasoning and Artificial Intelligence Mathematics (AI4Math), das große Modelle mit interaktiven Theorembeweisen (ITPs) kombiniert.
Das andere ist energieeffizientes maschinelles Lernen, das auf zeitlicher Logik basiert.
 Bild
Bild
Kaiyu Yang ist Postdoktorand im Department of Computational + Mathematical Sciences (CMS) am Caltech, betreut von Anima Anandkumar.
Er promovierte an der Princeton University, wo sein Betreuer Jia Deng war, und arbeitete auch mit Olga Russakovsky und Chen Danqi zusammen.
Seine Forschung konzentriert sich auf neurosymbolische künstliche Intelligenz, die darauf abzielt, maschinelles Lernen in die Lage zu versetzen, symbolisches Denken auszuführen, und hofft, dies durch zwei Richtungen zu erreichen:
(1) Wenden Sie maschinelles Lernen auf symbolische Denkaufgaben wie formale Logik an Oder mathematisches Denken und Beweisen von Theoremen in natürlicher Sprache.
(2) Führen Sie symbolische Komponenten in Modelle für maschinelles Lernen ein, um sie interpretierbarer, überprüfbarer und dateneffizienter zu machen.
Derzeit arbeitet er an künstlicher Intelligenz, die Mathematik verstehen und darüber nachdenken kann. Mathematische Argumentation ist ein wichtiger Meilenstein in der menschlichen Intelligenz und hat das Potenzial, viele wichtige Probleme in Wissenschaft und Technik zu verändern, wie etwa die Lösung partieller Differentialgleichungen und die Überprüfung von Formeln.
Anima Anandkumar ist jetzt Professorin für Computer- und Mathematikwissenschaften am Caltech.
 Bilder
Bilder
Ihre Forschungsinteressen konzentrieren sich hauptsächlich auf die Bereiche groß angelegtes maschinelles Lernen, nichtkonvexe Optimierung und hochdimensionale Statistik.
Insbesondere war sie Vorreiterin bei der Entwicklung und Analyse von Tensoralgorithmen für maschinelles Lernen.
Die Tensorzerlegungsmethode weist eine extrem hohe Parallelität und Skalierbarkeit auf und kann auf große Datenmengen angewendet werden. Es kann die Konvergenz zur optimalen Lösung garantieren und konsistente Schätzergebnisse für viele Wahrscheinlichkeitsmodelle (z. B. Markov-Modelle) ausgeben.
//m.sbmmt.com/link/1dd5a4016c624ef51f0542d4ae60e281
Das obige ist der detaillierte Inhalt vonCaltech-Chinesen nutzen KI, um mathematische Beweise zu untergraben! Beschleunigen Sie 5-mal schockiert Tao Zhexuan, 80 % der mathematischen Schritte sind vollständig automatisiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!