Große Modelle können ebenfalls in Scheiben geschnitten werden, und Microsoft SliceGPT erhöht die Recheneffizienz von LLAMA-2 erheblich

Groß angelegte Sprachmodelle (LLM) verfügen normalerweise über Milliarden von Parametern und werden auf Billionen von Token trainiert. Die Schulung und Bereitstellung solcher Modelle ist jedoch sehr teuer. Um den Rechenaufwand zu reduzieren, werden häufig verschiedene Modellkomprimierungstechniken eingesetzt.

Diese Modellkomprimierungstechniken können im Allgemeinen in vier Kategorien unterteilt werden: Destillation, Tensorzerlegung (einschließlich Faktorisierung mit niedrigem Rang), Bereinigung und Quantisierung. Pruning-Methoden gibt es schon seit einiger Zeit, aber viele erfordern nach dem Pruning eine Feinabstimmung der Wiederherstellung (Recovery Fine-Tuning, RFT), um die Leistung aufrechtzuerhalten, was den gesamten Prozess kostspielig und schwierig zu skalieren macht.

Forscher der ETH Zürich und von Microsoft haben eine Lösung für dieses Problem namens SliceGPT vorgeschlagen. Die Kernidee dieser Methode besteht darin, die Einbettungsdimension des Netzwerks durch Löschen von Zeilen und Spalten in der Gewichtsmatrix zu reduzieren, um die Leistung des Modells aufrechtzuerhalten. Das Aufkommen von SliceGPT bietet eine wirksame Lösung für dieses Problem.

Die Forscher stellten fest, dass sie mit SliceGPT große Modelle in wenigen Stunden mit einer einzigen GPU komprimieren konnten und so auch ohne RFT eine wettbewerbsfähige Leistung bei Generierungs- und Downstream-Aufgaben aufrechterhielten. Derzeit wurde die Forschung vom ICLR 2024 akzeptiert.

• Papiertitel: SLICEGPT: KOMPRIMIEREN SIE GROßE SPRACHENMODELLE DURCH LÖSCHEN VON ZEILEN UND SPALTEN
• Papierlink: https://arxiv.org/pdf/2401. .15024.pdf

Die Pruning-Methode funktioniert, indem sie bestimmte Elemente der Gewichtsmatrix im LLM auf Null setzt und umgebende Elemente zum Ausgleich selektiv aktualisiert. Dies führt zu einem spärlichen Muster, das einige Gleitkommaoperationen im Vorwärtsdurchlauf des neuronalen Netzwerks überspringt und so die Recheneffizienz verbessert.

Der Grad der Sparsity und der Sparsity-Modus sind Faktoren, die die relative Verbesserung der Rechengeschwindigkeit bestimmen. Wenn der Sparse-Modus sinnvoller ist, bringt er mehr Rechenvorteile. Im Gegensatz zu anderen Beschneidungsmethoden beschneidet SliceGPT, indem es ganze Zeilen oder Spalten der Gewichtsmatrix abschneidet (abschneidet!). Vor der Resektion durchläuft das Netzwerk eine Transformation, die die Vorhersagen unverändert lässt, aber leicht beeinflusste Scherprozesse zulässt.

Die Folge ist, dass die Gewichtsmatrix reduziert, die Signalübertragung geschwächt und die Dimension des neuronalen Netzwerks verringert wird.

Abbildung 1 unten vergleicht die SliceGPT-Methode mit vorhandenen Sparsity-Methoden.

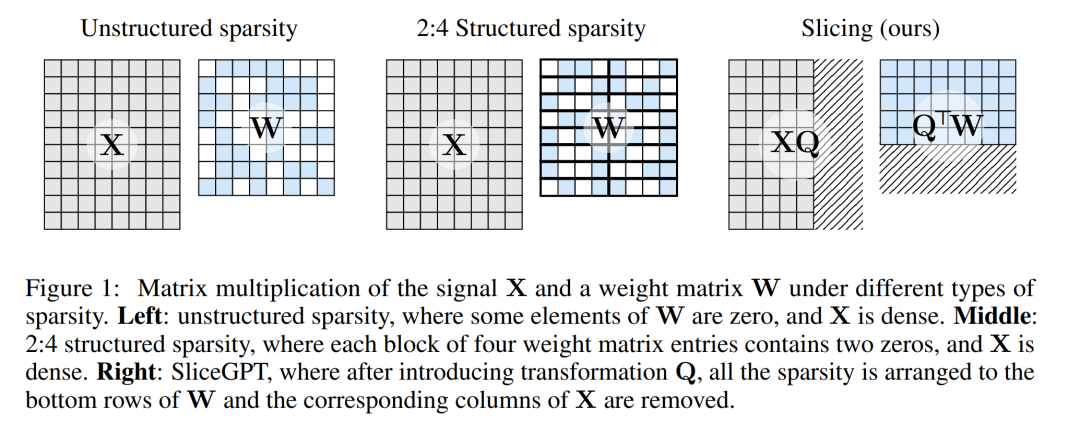
Durch umfangreiche Experimente haben die Autoren herausgefunden, dass SliceGPT bis zu 25 % der Modellparameter (einschließlich Einbettungen) für LLAMA-2 70B-, OPT 66B- und Phi-2-Modelle entfernen kann, während 99 % davon beibehalten werden dichte Modelle, 99 % bzw. 90 % Null-Stichproben-Aufgabenleistung.

Von SliceGPT verarbeitete Modelle können auf weniger GPUs und schneller ausgeführt werden, ohne dass zusätzliche Codeoptimierung erforderlich ist: Auf einer 24-GB-GPU für Endverbraucher verglich der Autor die gesamte Inferenzberechnung von LLAMA-2 mit 70 B. Der Betrag wurde auf 64 % reduziert. beim dichten Modell; bei der 40-GB-A100-GPU wurde sie auf 66 % reduziert.

Darüber hinaus schlugen sie auch ein neues Konzept vor, die rechnerische Invarianz in Transformer-Netzwerken, das SliceGPT ermöglicht.

SliceGPT im Detail

Die SliceGPT-Methode basiert auf der rechnerischen Invarianz, die der Transformer-Architektur innewohnt. Das bedeutet, dass Sie eine orthogonale Transformation auf die Ausgabe einer Komponente anwenden und diese dann in der nächsten Komponente rückgängig machen können. Die Autoren stellten fest, dass zwischen Netzwerkblöcken durchgeführte RMSNorm-Operationen keinen Einfluss auf die Transformation haben: Diese Operationen sind kommutativ.

In dem Artikel stellt der Autor zunächst vor, wie man mit RMSNorm-Verbindungen Invarianz in einem Transformer-Netzwerk erreicht, und erklärt dann, wie man ein mit LayerNorm-Verbindungen trainiertes Netzwerk in RMSNorm umwandelt. Als nächstes stellen sie die Methode vor, die Hauptkomponentenanalyse (PCA) zu verwenden, um die Transformation jeder Schicht zu berechnen und so das Signal zwischen Blöcken auf seine Hauptkomponenten zu projizieren. Schließlich zeigen sie, wie das Entfernen kleinerer Hauptkomponenten dem Abschneiden von Zeilen oder Spalten des Netzwerks entspricht.

Rechnerinvarianz des Transformer-Netzwerks

Verwenden Sie Q, um die orthogonale Matrix darzustellen: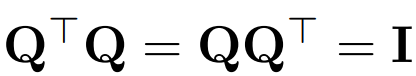

• Beachten Sie, dass das Multiplizieren eines Vektors

Angenommen, X_ℓ ist die Ausgabe eines Transformatorblocks. Nach der Verarbeitung durch RMSNorm wird sie in Form von RMSNorm (X_ℓ) in den nächsten Block eingegeben. Wenn Sie eine lineare Schicht mit einer orthogonalen Matrix Q vor RMSNorm und Q^⊤ nach RMSNorm einfügen, bleibt das Netzwerk unverändert, da jede Zeile der Signalmatrix mit Q multipliziert, normalisiert und mit Q^ ⊤ multipliziert wird. Hier haben wir:

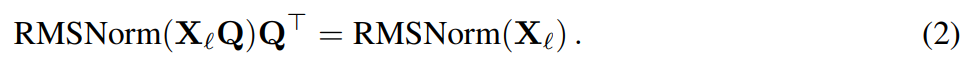
Da nun jeder Aufmerksamkeits- oder FFN-Block im Netzwerk eine lineare Operation am Ein- und Ausgang ausführt, kann die zusätzliche Operation Q in die lineare Schicht des Moduls aufgenommen werden. Da das Netzwerk Restverbindungen enthält, muss Q auch auf die Ausgänge aller vorherigen Schichten (bis zur Einbettung) und aller nachfolgenden Schichten (bis zum LM-Kopf) angewendet werden.

Eine invariante Funktion bezieht sich auf eine Funktion, deren Eingabetransformation keine Änderung der Ausgabe verursacht. Im Beispiel dieses Artikels kann jede orthogonale Transformation Q auf die Gewichte des Transformators angewendet werden, ohne das Ergebnis zu ändern, sodass die Berechnung in jedem Transformationszustand durchgeführt werden kann. Die Autoren nennen diese rechnerische Invarianz und definieren sie im folgenden Satz.

Theorem 1: Sei 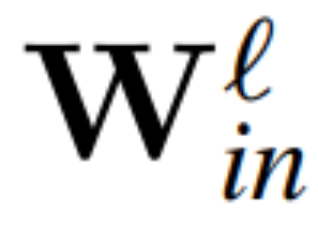und 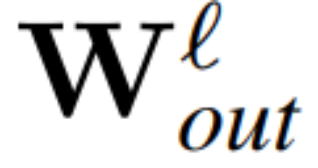die Gewichtsmatrix der linearen Schicht des ℓ-ten Blocks des Transformatornetzwerks, die durch RMSNorm verbunden ist, 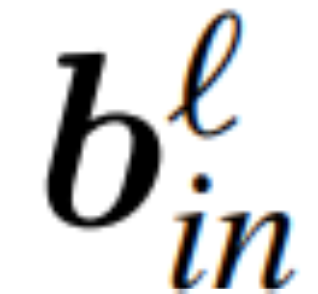und 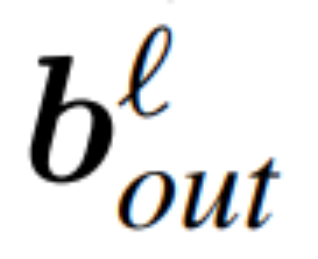seien die entsprechenden Bias (falls vorhanden), W_embd und W_head seien die Einbettungsmatrix und Kopfmatrix. Angenommen, Q ist eine orthogonale Matrix mit der Dimension D, dann entspricht das folgende Netzwerk dem ursprünglichen Transformatornetzwerk:

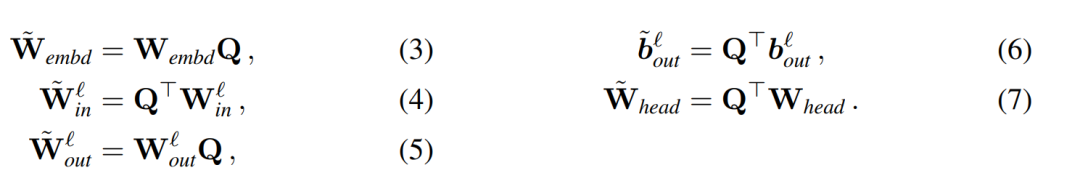
Das Kopieren der Eingangsvorspannung und der Kopfvorspannung:

kann über den Algorithmus erfolgen 1, um zu beweisen, dass das konvertierte Netzwerk dieselben Ergebnisse berechnet wie das ursprüngliche Netzwerk.

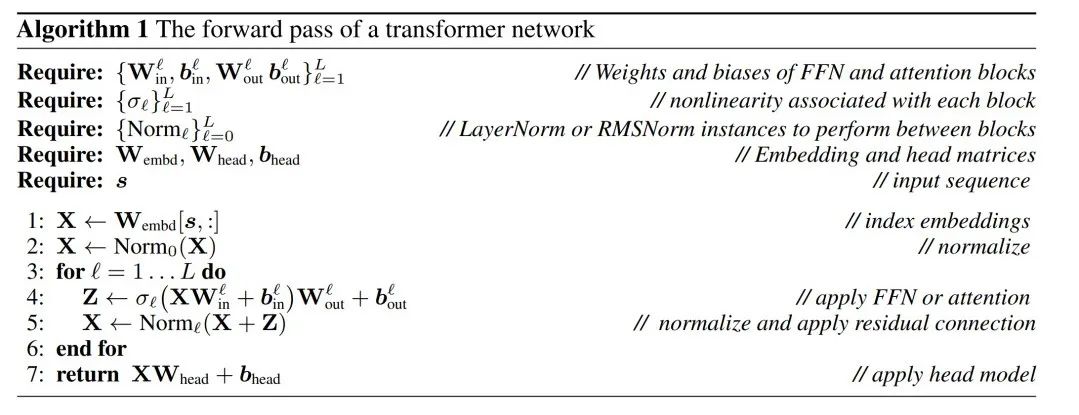
LayerNorm Transformer kann in RMSNorm umgewandelt werden

Transformer Die rechnerische Invarianz des Netzwerks gilt nur für mit RMSNorm verbundene Netzwerke. Bevor ein Netzwerk mit LayerNorm verarbeitet wird, konvertieren die Autoren das Netzwerk zunächst in RMSNorm, indem sie lineare Blöcke von LayerNorm in benachbarte Blöcke absorbieren.

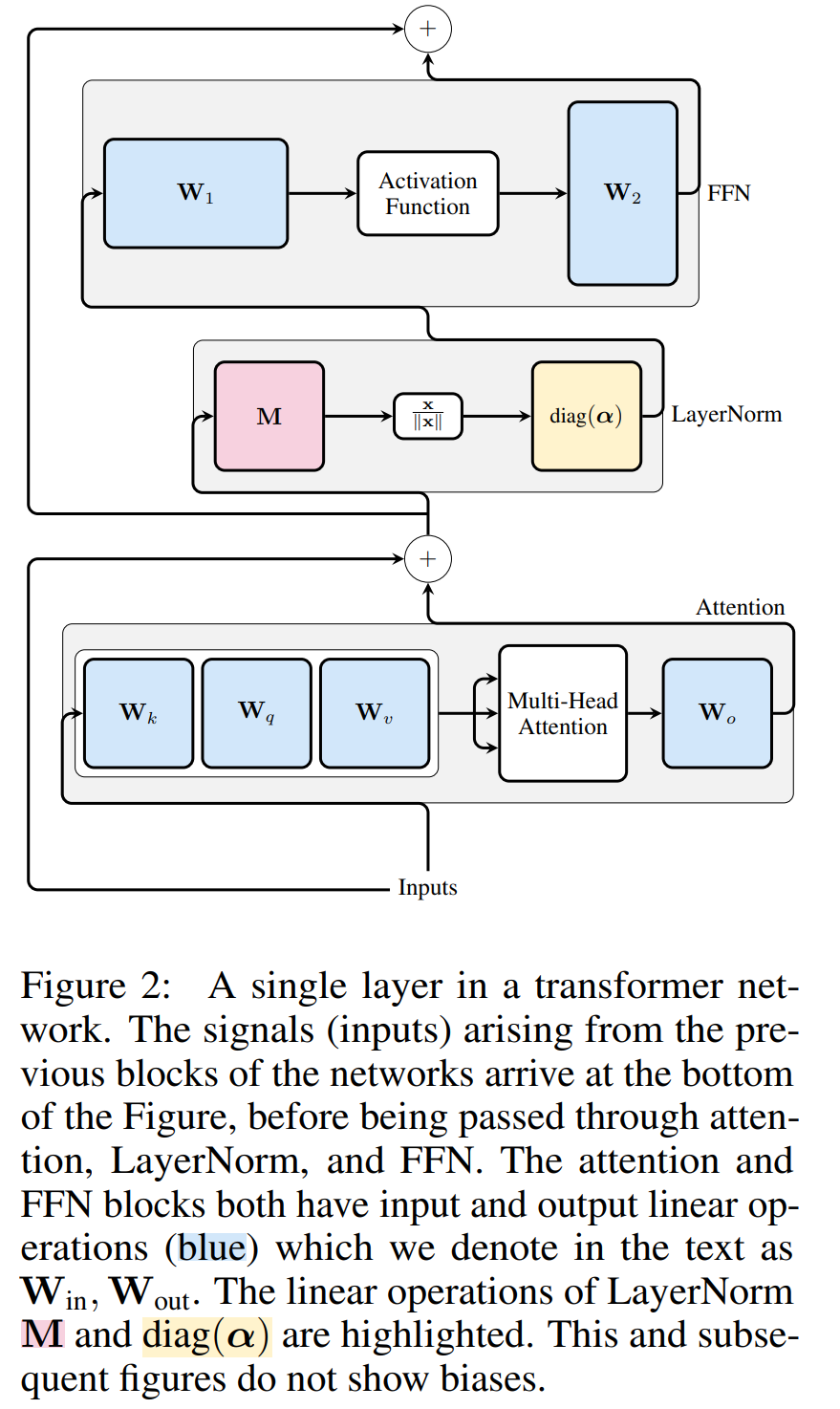
Abbildung 3 zeigt diese Transformation des Transformer-Netzwerks (siehe Abbildung 2). In jedem Block multiplizieren die Autoren die Ausgabematrix W_out mit der mittleren Subtraktionsmatrix M, die die mittlere Subtraktion in der nachfolgenden LayerNorm berücksichtigt. Die Eingabematrix W_in wird mit dem Anteil des vorherigen LayerNorm-Blocks vormultipliziert. Die Einbettungsmatrix W_embd muss einer mittleren Subtraktion unterzogen werden und W_head muss entsprechend dem Anteil der letzten LayerNorm neu skaliert werden. Dies ist eine einfache Änderung der Reihenfolge der Vorgänge und hat keinen Einfluss auf die Netzwerkausgabe.

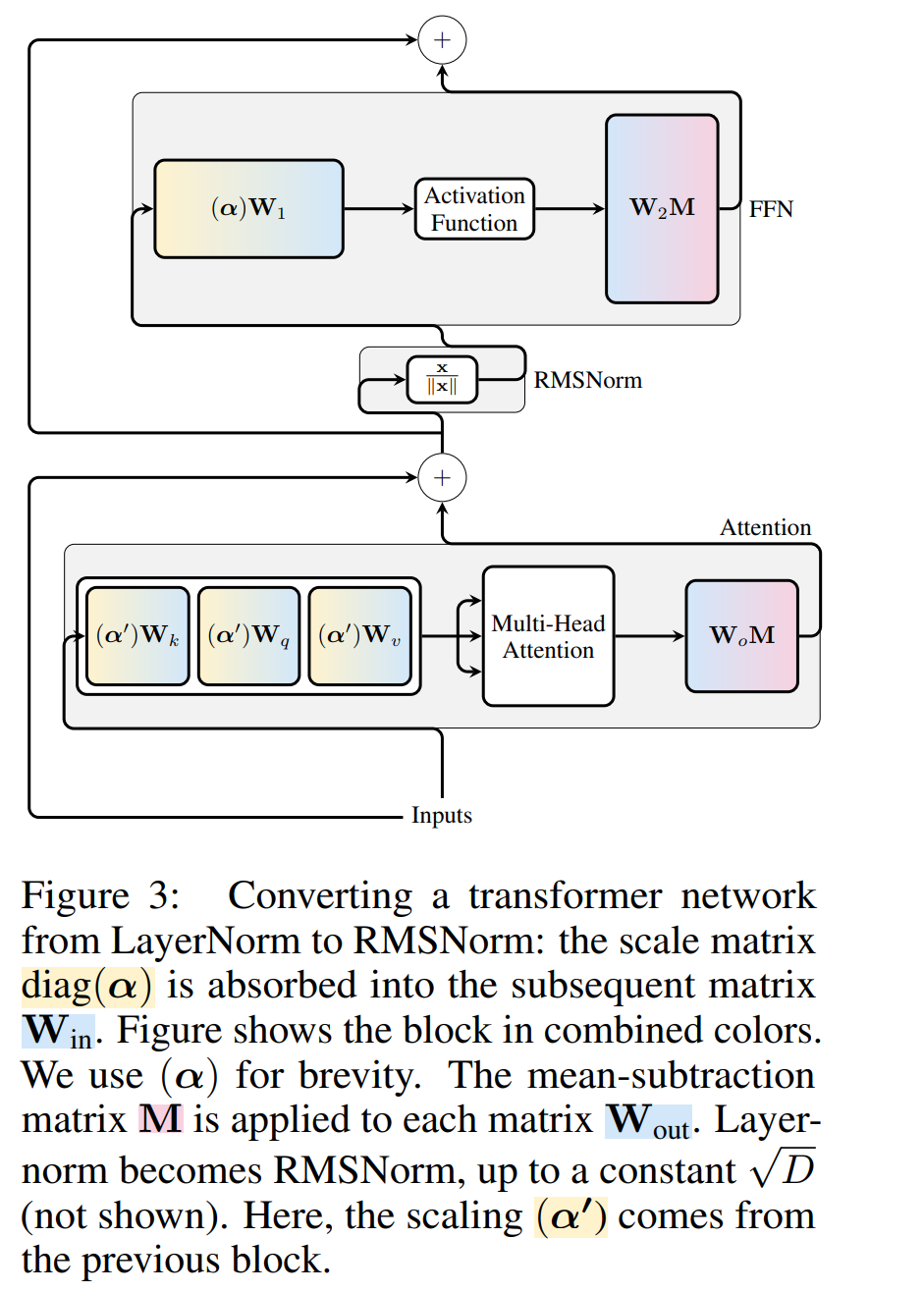
Transformation jedes Blocks

Da nun jede LayerNorm im Transformator in RMSNorm konvertiert wurde, kann ein beliebiges Q ausgewählt werden, um das Modell zu ändern. Der ursprüngliche Plan des Autors bestand darin, Signale aus dem Modell zu sammeln, diese Signale zum Aufbau einer orthogonalen Matrix zu verwenden und dann Teile des Netzwerks zu löschen. Sie stellten schnell fest, dass die Signale von verschiedenen Blöcken im Netzwerk nicht ausgerichtet waren, sodass sie auf jeden Block eine andere orthogonale Matrix oder Q_ℓ anwenden mussten.

Wenn die in jedem Block verwendete orthogonale Matrix unterschiedlich ist, ändert sich das Modell nicht. Die Beweismethode ist dieselbe wie bei Satz 1, mit Ausnahme von Zeile 5 von Algorithmus 1. Hier sieht man, dass der Ausgang der Restverbindung und der Block die gleiche Drehung haben müssen. Um dieses Problem zu lösen, modifiziert der Autor die Restverbindung, indem er den Rest linear transformiert.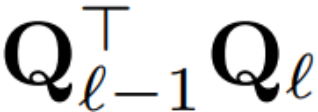

Abbildung 4 zeigt, wie unterschiedliche Drehungen an verschiedenen Blöcken durchgeführt werden, indem zusätzliche lineare Operationen an der Restverbindung ausgeführt werden. Im Gegensatz zu Änderungen an der Gewichtsmatrix können diese zusätzlichen Operationen nicht vorberechnet werden und fügen dem Modell einen geringen Overhead (D × D) hinzu. Dennoch sind diese Vorgänge erforderlich, um das Modell wegzuschneiden, und Sie können sehen, dass die Gesamtgeschwindigkeit tatsächlich zunimmt.

Zur Berechnung der Matrix Q_ℓ verwendete der Autor PCA. Sie wählen einen Kalibrierungsdatensatz aus dem Trainingssatz aus, lassen ihn durch das Modell laufen (nachdem sie die LayerNorm-Operation in RMSNorm konvertiert haben) und extrahieren die orthogonale Matrix für diese Ebene. Genauer gesagt, wenn sie die Ausgabe des transformierten Netzwerks verwenden, um die orthogonale Matrix der nächsten Schicht zu berechnen. Genauer gesagt, wenn 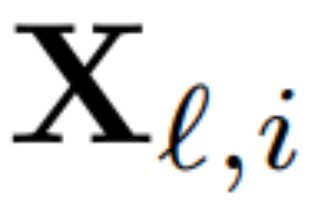die Ausgabe des ℓ-ten RMSNorm-Moduls für die i-te Sequenz im Kalibrierungsdatensatz ist, berechnen Sie: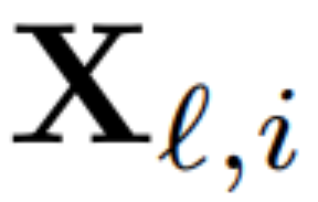

und setzen Sie Q_ℓ als abnehmenden Eigenvektor von C_ℓ in Eigenwerten Sortieren.成 Entfernung 分 Das Ziel der Hauptkomponentenanalyse besteht darin, die Datenmatrix eine kleine D × D-Deletionsmatrix (die D kleine Spalten der D × D-Homotopenmatrix enthält), die zum Löschen einiger Spalten auf der linken Seite der Matrix verwendet wird. Die Rekonstruktion ist L_2-optimal in dem Sinne, dass QD eine lineare Karte ist, die minimiert.

Beim Anwenden von PCA auf die Interblock-Signalmatrix In der obigen Operation wurde diese Matrix mit Q multipliziert. Der Autor hat die Zeile von W_in und die Spalten von W_out und W_embd entfernt. Sie entfernten auch die Zeilen und Spalten der Matrix , die in die Restverbindung eingefügt wurden (siehe Abbildung 4). Experimentelle Ergebnisse Datensatz. Tabelle 1 zeigt die Komplexität, die nach verschiedenen Bereinigungsstufen des Modells erhalten bleibt. Im Vergleich zum LLAMA-2-Modell zeigte SliceGPT bei der Anwendung auf das OPT-Modell eine überlegene Leistung, was mit den Spekulationen des Autors auf der Grundlage der Analyse des Modellspektrums übereinstimmt.

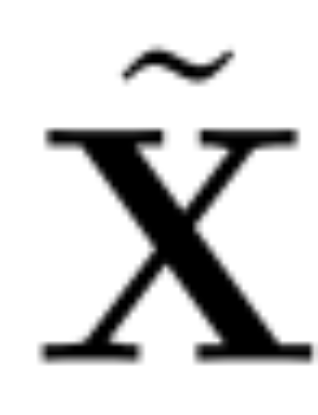Die Leistung von SliceGPT verbessert sich mit zunehmender Modellgröße. Der SparseGPT 2:4-Modus schneidet bei allen Modellen der LLAMA-2-Serie mit 25 % Clipping schlechter ab als SliceGPT. Für OPT kann festgestellt werden, dass die Sparsität des Modells mit einem Resektionsverhältnis von 30 % in allen Modellen mit Ausnahme des 2,7B-Modells besser ist als die von 2:4.

Zero-Sample-Aufgabe

Der Autor verwendete fünf Aufgaben: PIQA, WinoGrande, HellaSwag, ARC-e und ARCc, um die Leistung von SliceGPT bei der Zero-Sample-Aufgabe zu bewerten. Als Standard verwendete er LM Evaluation Harness im Bewertungsparameter.

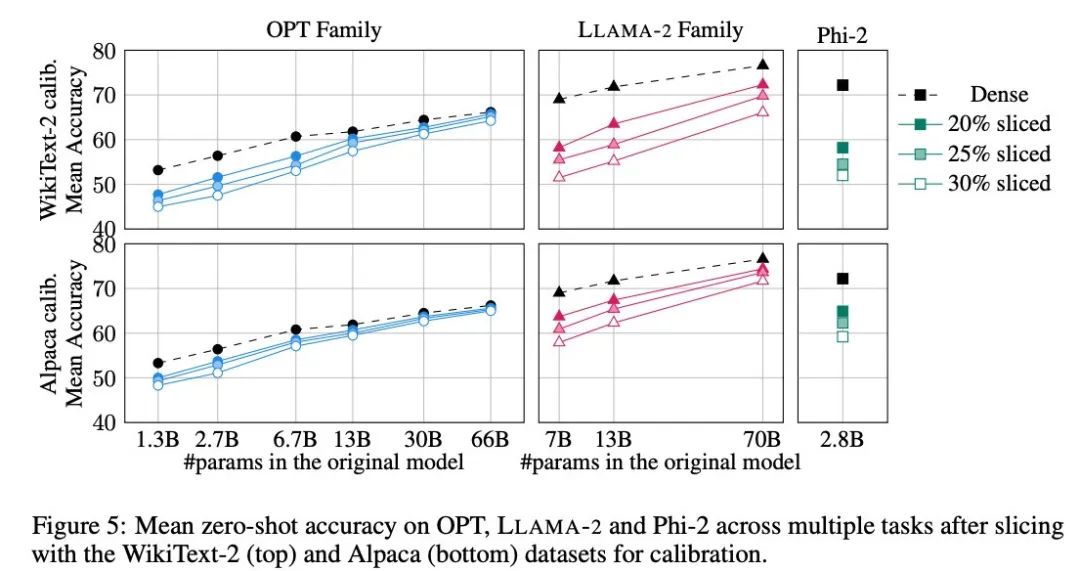
Abbildung 5 zeigt die durchschnittlichen Ergebnisse, die das maßgeschneiderte Modell bei den oben genannten Aufgaben erzielt. Die obere Reihe der Abbildung zeigt die durchschnittliche Genauigkeit von SliceGPT in WikiText-2 und die untere Reihe zeigt die durchschnittliche Genauigkeit von SliceGPT in Alpaca. Aus den Ergebnissen lassen sich ähnliche Schlussfolgerungen wie bei der Generierungsaufgabe ziehen: Das OPT-Modell lässt sich besser an die Komprimierung anpassen als das LLAMA-2-Modell, und je größer das Modell, desto weniger offensichtlich ist der Rückgang der Genauigkeit nach dem Bereinigen.

Der Autor hat die Wirkung von SliceGPT an einem kleinen Modell wie Phi-2 getestet. Das getrimmte Phi-2-Modell weist eine vergleichbare Leistung wie das getrimmte LLAMA-2 7B-Modell auf. Die größten OPT- und LLAMA-2-Modelle können effizient komprimiert werden, und SliceGPT verliert nur wenige Prozentpunkte, wenn 30 % aus dem 66B-OPT-Modell entfernt werden.

Der Autor führte auch ein Experiment zur Wiederherstellung der Feinabstimmung (RFT) durch. Eine kleine Anzahl von RFTs wurde mit LoRA an den getrimmten LLAMA-2- und Phi-2-Modellen durchgeführt.

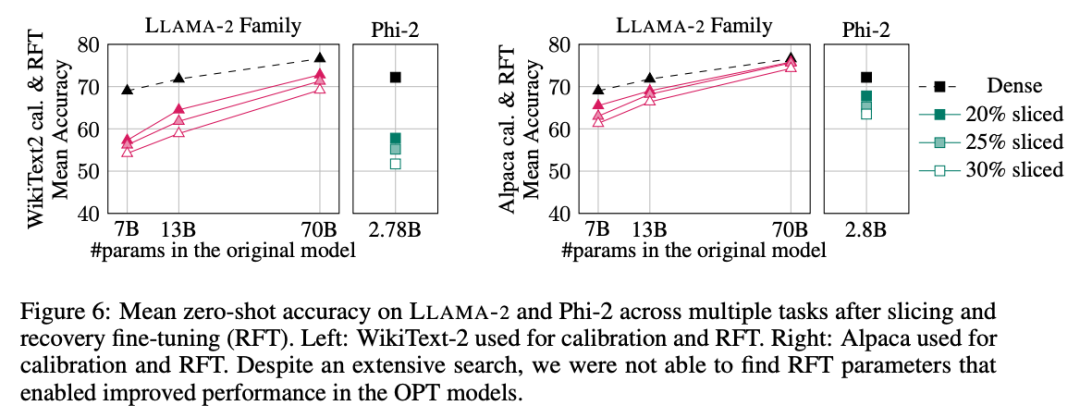
Die experimentellen Ergebnisse sind in Abbildung 6 dargestellt. Es lässt sich feststellen, dass es erhebliche Unterschiede in den RFT-Ergebnissen zwischen den WikiText-2- und Alpaca-Datensätzen gibt und das Modell im Alpaca-Datensatz eine bessere Leistung zeigt. Die Autoren glauben, dass der Grund für den Unterschied darin liegt, dass die Aufgaben im Alpaca-Datensatz näher an den Basisaufgaben liegen.

Für das größte LLAMA-2 70B-Modell beträgt die endgültige durchschnittliche Genauigkeit im Alpaka-Datensatz nach 30 % Beschneidung und Durchführung von RFT 74,3 % und die Genauigkeit des ursprünglichen dichten Modells 76,6 %. Das maßgeschneiderte Modell LLAMA-2 70B behält etwa 51,6B-Parameter bei und sein Durchsatz ist deutlich verbessert.

Der Autor stellte außerdem fest, dass Phi-2 die ursprüngliche Genauigkeit des beschnittenen Modells im WikiText-2-Datensatz nicht wiederherstellen konnte, aber einige Prozentpunkte der Genauigkeit im Alpaka-Datensatz wiederherstellen konnte. Phi-2, um 25 % gekürzt und RFTed, weist im Alpaca-Datensatz eine durchschnittliche Genauigkeit von 65,2 % auf, und die Genauigkeit des ursprünglichen dichten Modells beträgt 72,2 %. Das getrimmte Modell behält 2,2B-Parameter und 90,3 % der Genauigkeit des 2,8B-Modells. Dies zeigt, dass selbst kleine Sprachmodelle effektiv beschnitten werden können.

Benchmark-Durchsatz

Im Gegensatz zu herkömmlichen Beschneidungsmethoden führt SliceGPT (strukturierte) Sparsität in der Matrix X ein: Die gesamte Spalte X wird abgeschnitten, wodurch die Einbettungsdimension verringert wird. Dieser Ansatz erhöht sowohl die Rechenkomplexität (Anzahl der Gleitkommaoperationen) des SliceGPT-Komprimierungsmodells als auch die Effizienz der Datenübertragung.

Stellen Sie auf einer 80-GB-H100-GPU die Sequenzlänge auf 128 ein und verdoppeln Sie die Sequenzlänge stapelweise, um den maximalen Durchsatz zu ermitteln, bis der GPU-Speicher erschöpft ist oder der Durchsatz sinkt. Die Autoren verglichen den Durchsatz von auf 25 % und 50 % bereinigten Modellen mit dem ursprünglichen dichten Modell auf einer 80-GB-H100-GPU. Modelle, die um 25 % verkleinert wurden, erzielten eine bis zu 1,55-fache Durchsatzverbesserung.

Mit 50 % Clipping erreicht das größte Modell mit einer einzigen GPU erhebliche Durchsatzsteigerungen von 3,13x und 1,87x. Dies zeigt, dass der Durchsatz des bereinigten Modells das 6,26-fache bzw. das 3,75-fache des ursprünglichen dichten Modells erreicht, wenn die Anzahl der GPUs festgelegt ist.

Nach 50 % Bereinigung ist die von SliceGPT in WikiText2 beibehaltene Komplexität zwar schlechter als bei SparseGPT 2:4, der Durchsatz übertrifft jedoch die SparseGPT-Methode bei weitem. Bei Modellen der Größe 13B kann sich der Durchsatz auch bei kleineren Modellen auf Consumer-GPUs mit weniger Speicher verbessern.

Inferenzzeit

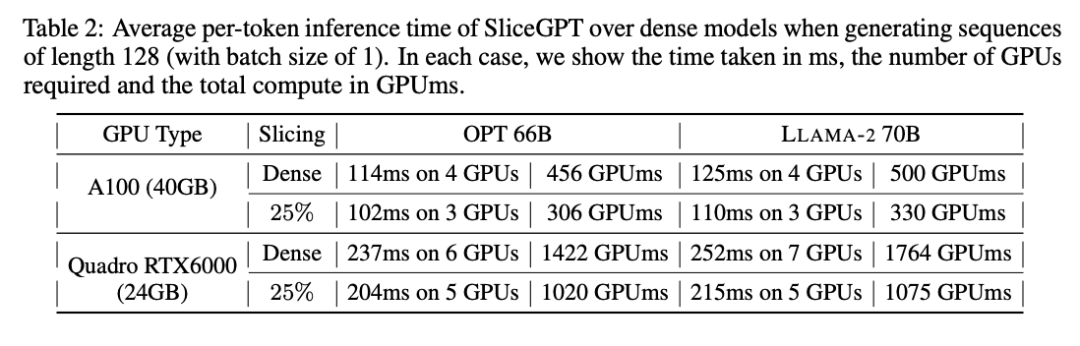
Der Autor untersuchte auch die End-to-End-Laufzeit des mit SliceGPT komprimierten Modells. Tabelle 2 vergleicht die Zeit, die zum Generieren eines einzelnen Tokens für die Modelle OPT 66B und LLAMA-2 70B auf Quadro RTX6000- und A100-GPUs erforderlich ist. Es lässt sich feststellen, dass bei der RTX6000-GPU nach der Reduzierung des Modells um 25 % die Inferenzgeschwindigkeit um 16–17 % erhöht wird; bei der A100-GPU wird die Geschwindigkeit um 11–13 % erhöht. Für LLAMA-2 70B ist der Rechenaufwand mit der RTX6000-GPU im Vergleich zum ursprünglichen dichten Modell um 64 % reduziert. Der Autor führt diese Verbesserung darauf zurück, dass SliceGPT die ursprüngliche Gewichtsmatrix durch eine kleinere Gewichtsmatrix ersetzt und dichte Kernel verwendet, was mit anderen Bereinigungsschemata nicht erreicht werden kann.

Die Autoren gaben an, dass ihr Basiswert SparseGPT 2:4 zum Zeitpunkt des Schreibens keine durchgängigen Leistungsverbesserungen erzielen konnte. Stattdessen verglichen sie SliceGPT mit SparseGPT 2:4, indem sie die relative Zeit jeder Operation in der Transformatorschicht verglichen. Sie fanden heraus, dass SliceGPT (25 %) bei großen Modellen hinsichtlich Geschwindigkeitsverbesserung und Verwirrung mit SparseGPT (2:4) konkurrenzfähig war.

Rechenkosten

Alle LLAMA-2-, OPT- und Phi-2-Modelle können in 1 bis 3 Stunden auf einer einzigen GPU segmentiert werden. Wie in Tabelle 3 gezeigt, können mit der Feinabstimmung der Wiederherstellung alle LMs innerhalb von 1 bis 5 Stunden komprimiert werden.

Weitere Informationen finden Sie im Originalpapier.

Das obige ist der detaillierte Inhalt vonGroße Modelle können ebenfalls in Scheiben geschnitten werden, und Microsoft SliceGPT erhöht die Recheneffizienz von LLAMA-2 erheblich. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!