Nach der letzten Bestandsaufnahme von „11 Basisdiagramme, die Datenwissenschaftler in 95 % der Fälle verwenden“ stellen wir Ihnen heute 11 Basisverteilungen vor, die Datenwissenschaftler in 95 % der Fälle verwenden. Die Beherrschung dieser Verteilungen hilft uns, die Natur der Daten besser zu verstehen und bei der Datenanalyse und Entscheidungsfindung genauere Schlussfolgerungen und Vorhersagen zu treffen.
Normalverteilung, auch als Gaußsche Verteilung bekannt, ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Es hat eine symmetrische glockenförmige Kurve mit dem Mittelwert (μ) als Mittelpunkt und der Standardabweichung (σ) als Breite. Die Normalverteilung hat in vielen Bereichen wie Statistik, Wahrscheinlichkeitstheorie und Ingenieurwesen einen wichtigen Anwendungswert.
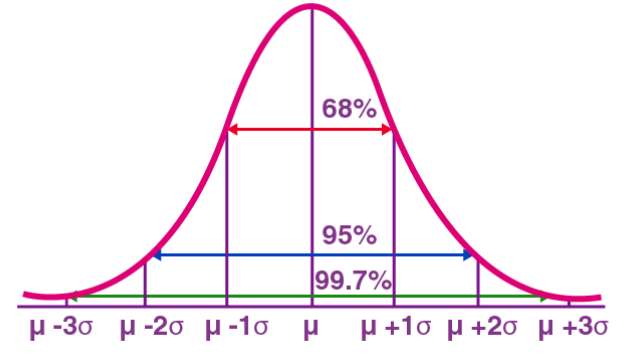
Die Wahrscheinlichkeitsdichtefunktion der Normalverteilung kann ausgedrückt werden als:
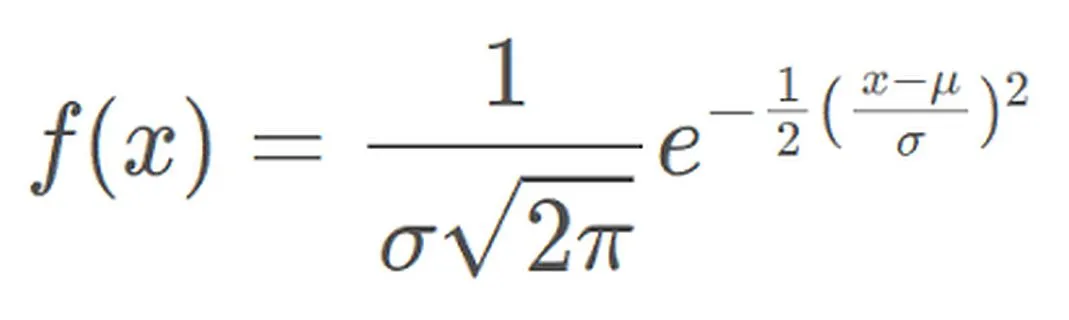
Die Wahrscheinlichkeitsdichtefunktion stellt die Wahrscheinlichkeitsdichte der Werte einer normalverteilten Zufallsvariablen im Einheitsintervall in der Nähe eines bestimmten Werts dar X. Unter diesen stellt μ den Mittelwert und σ die Standardabweichung dar. Die Normalverteilung wird in der Praxis häufig verwendet. Beispielsweise nähert sich die Verteilung der menschlichen Größe und des menschlichen Gewichts einer Normalverteilung an. Darüber hinaus sind Testergebnisse häufig normalverteilt, wobei weniger Personen hohe und niedrige Werte erzielen und mehr Personen im mittleren Bereich abschneiden. Dieses Verteilungsmodell hat in vielen Bereichen einen wichtigen Anwendungswert
2. Die Bernoulli-Verteilung (Bernoulli-Verteilung) ist eine diskrete Wahrscheinlichkeitsverteilung, die zur Beschreibung eines einzelnen Ereignisses mit nur zwei möglichen Ergebnissen verwendet wird. Bei Bernoulli-Versuchen kann es um Kopf oder Zahl, Erfolg oder Misserfolg, Ja oder Nein usw. gehen. Zum Beispiel eine Münze werfen, testen, ob ein Produkt qualifiziert ist, ob jemand ein bestimmtes Produkt kauft usw.
Die Wahrscheinlichkeitsmassenfunktion der Bernoulli-Verteilung ist: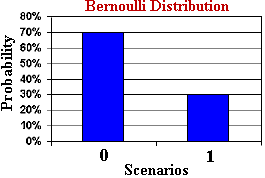
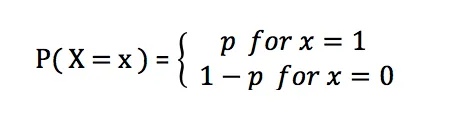Anwendung der Bernoulli-Verteilung in der Praxis: Beispielsweise besteht die Binomialverteilung aus n unabhängigen wiederholten Experimenten der Bernoulli-Verteilung.
3. Binomialverteilung
Binomialverteilung (Binomialverteilung) ist eine diskrete Wahrscheinlichkeitsverteilung, die zur Beschreibung der Wahrscheinlichkeitsverteilung der Anzahl von Erfolgen in n unabhängigen wiederholten Experimenten verwendet wird. Jeder Versuch hat nur zwei mögliche Ergebnisse: Erfolg (aufgezeichnet als 1) oder Misserfolg (aufgezeichnet als 0). Die Erfolgswahrscheinlichkeit beträgt p und die Misserfolgswahrscheinlichkeit 1-p.
Die Wahrscheinlichkeitsmassenfunktion der Binomialverteilung kann ausgedrückt werden als: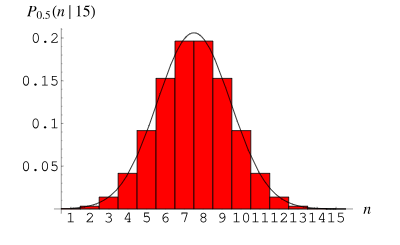
die Anzahl der Kombinationen ist, die die Auswahl angibt k aus n Versuchen Die Anzahl erfolgreicher Kombinationen. p ist die Erfolgswahrscheinlichkeit im Bereich von 0 bis 1. n ist die Anzahl der Versuche.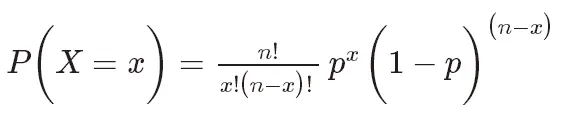
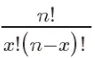
Hier stellt P(X=k) die Wahrscheinlichkeit dar, dass ein Ereignis k-mal innerhalb eines festen Zeitraums auftritt, und λ stellt die durchschnittliche Auftrittsrate eines Ereignisses dar, also die durchschnittliche Anzahl von Ereignissen, die pro Zeiteinheit auftreten. e ist eine natürliche Konstante, die ungefähr 2,718 entspricht. k stellt die Anzahl der auftretenden Ereignisse dar. In einem Callcenter kann die Anzahl der Anrufe beispielsweise als Poisson-Verteilung betrachtet werden, wobei die durchschnittliche Anzahl der Anrufe pro Minute λ
ist5. Exponentialverteilung
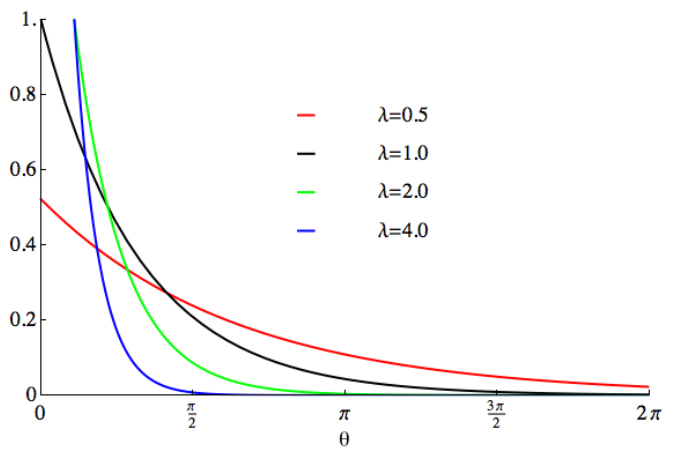Die Wahrscheinlichkeitsdichtefunktion der Exponentialverteilung ist:
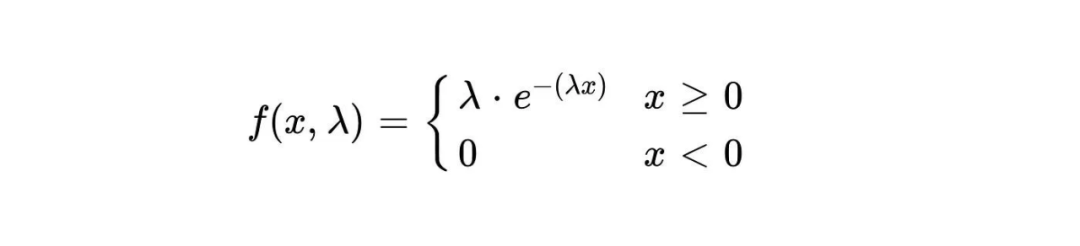Die Wahrscheinlichkeitsdichte eines Ereignisses, das innerhalb einer bestimmten Zeit x auftritt, wird durch f(x,λ) dargestellt. λ stellt die durchschnittliche Auftrittsrate von Ereignissen dar, also die durchschnittliche Anzahl von Ereignissen, die pro Zeiteinheit auftreten. e ist eine natürliche Konstante, die ungefähr 2,718 entspricht. Die Exponentialverteilung hat im wirklichen Leben viele Anwendungen. Beispielsweise können beim radioaktiven Zerfall die Zerfallszeiten radioaktiver Kerne als exponentiell verteilt angesehen werden. Dies bedeutet, dass die Wahrscheinlichkeitsverteilung der Abklingzeiten einer Exponentialfunktion folgt. Die durchschnittliche Abklingzeit entspricht dem Parameter λ der Exponentialfunktion
6. Gammaverteilung
Gammaverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die verwendet wird, um die Wahrscheinlichkeit des Auftretens eines Ereignisses innerhalb einer bestimmten Zeit zu beschreiben. Dies gilt für Situationen, in denen Ereignisse unabhängig voneinander sind und die durchschnittliche Auftrittsrate immer konstant ist. Die Wahrscheinlichkeitsdichtefunktion der Gammaverteilung lautet:
wobei f(x) die Zeit x zu einem bestimmten Zeitpunkt darstellt Wahrscheinlichkeitsdichte interner Ereignisse. α und β sind die Formparameter und Geschwindigkeitsparameter der Gammaverteilung. α wird verwendet, um die Form der Gammaverteilung zu bestimmen, und sein Wert reicht von 0 bis positiv unendlich. β stellt die durchschnittliche Auftretensrate von Ereignissen dar, dh die durchschnittliche Anzahl von Ereignissen, die pro Zeiteinheit auftreten, und der Wertebereich reicht von 0 bis positiv unendlich. e ist eine natürliche Konstante, die ungefähr 2,718 entspricht. Praktische Anwendungen der Gammaverteilung: Zum Beispiel radioaktiver Zerfall: Beim radioaktiven Zerfall kann die Zeit, die radioaktive Kerne zum Zerfall benötigen, als Gammaverteilung betrachtet werden, und die durchschnittliche Zerfallszeit beträgt β/. α.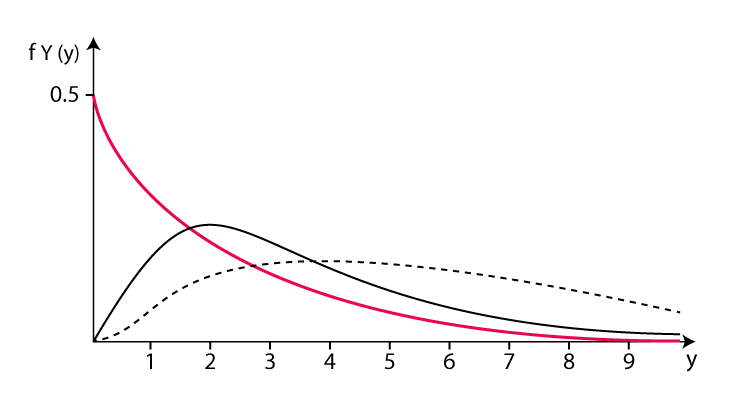
7. Beta-Verteilung
Beta-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die verwendet wird, um die Wahrscheinlichkeitsverteilung der Anzahl von Erfolgen in einer Menge von Werten zu beschreiben. Es verfügt über zwei Parameter, die den Erwartungswert (Mittelwert) und die Standardabweichung (Standardabweichung) der Erfolgswahrscheinlichkeit darstellen.
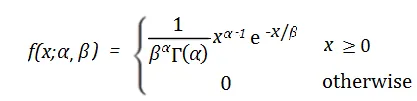
Die Wahrscheinlichkeitsdichtefunktion der Beta-Verteilung lautet wie folgt:
Dabei stellt x die Anzahl der Erfolge dar, α und β stellen jeweils die Formparameter der Verteilung dar Die Beta-Verteilung hat Anwendungen in vielen praktischen Problemen. Bei der Genbearbeitung könnten Forscher beispielsweise eine Betaverteilung verwenden, um die Wahrscheinlichkeit vorherzusagen, dass eine Genbearbeitungstechnologie eine bestimmte Zielstelle erfolgreich bearbeiten wird. Im Finanzbereich kann die Betaverteilung zur Beschreibung der Volatilität von Vermögenspreisen oder zur Berechnung der erwarteten Rendite eines Anlageportfolios verwendet werden.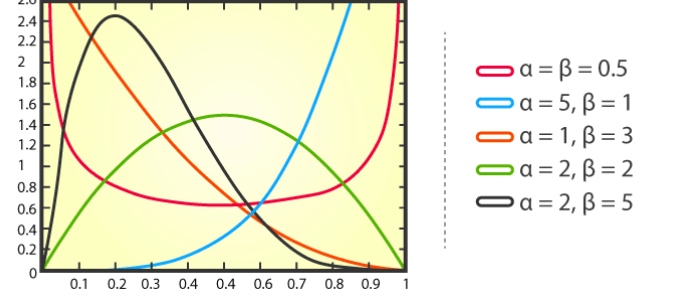
8 Gleichmäßige Verteilung
Die Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, die zur Beschreibung einer Menge verwendet wird von Werten in einem bestimmten Intervall gleichmäßig verteilt. Es gibt zwei Arten von Gleichverteilungen: diskrete Gleichverteilung und kontinuierliche Gleichverteilung.
Diskrete Gleichverteilung: Wenn eine diskrete Zufallsvariable vorliegt, folgt sie einer diskreten Gleichverteilung. Kontinuierliche Gleichverteilung: Wenn die Wahrscheinlichkeitsdichtefunktion einer kontinuierlichen Zufallsvariablen auftreten. Wenn Sie beispielsweise eine faire Münze werfen, beträgt die Wahrscheinlichkeit von Kopf und Zahl 1/2, was einer gleichmäßigen Verteilung entspricht.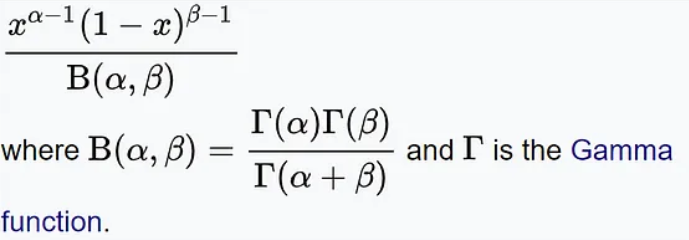
Die Log-Normalverteilung (Log-Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die dadurch gekennzeichnet ist, dass der Logarithmus der Zufallsvariablen der Normalverteilung folgt. Mit anderen Worten: Wenn der Logarithmus ln(X) einer Zufallsvariablen X der Normalverteilung folgt, dann folgt die Zufallsvariable X der Lognormalverteilung.
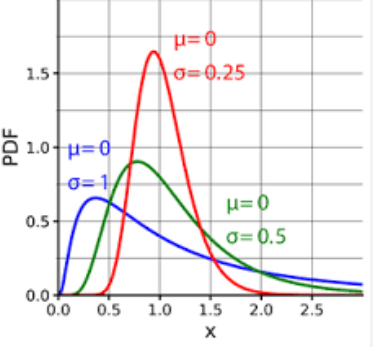
Die Wahrscheinlichkeitsdichtefunktion der Lognormalverteilung kann ausgedrückt werden als:
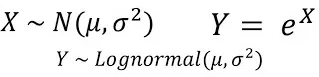
wobei μ der Mittelwert der Lognormalverteilung und σ die Standardabweichung der Lognormalverteilung ist.
Die logarithmische Normalverteilung ist in vielen praktischen Anwendungen von großer Bedeutung, beispielsweise im Finanzwesen (Aktienkurse, Renditen usw.), in der Biologie (Wachstumsrate usw.), in der Wirtschaft (Verbraucherausgaben usw.) usw.
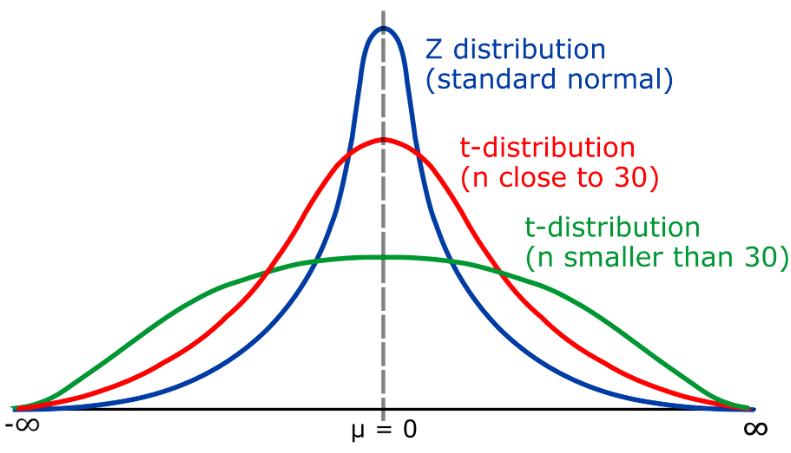
T-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die hauptsächlich zur Beschreibung der Mittelwertverteilung bei kleinen Stichproben verwendet wird. Die t-Verteilung ähnelt der Normalverteilung, ihr Ende kann sich jedoch je nach Freiheitsgrad (k) nach links und rechts erstrecken. Die t-Verteilung wird häufig bei statistischen Schlussfolgerungen verwendet, beispielsweise beim Testen von Hypothesen, um den signifikanten Unterschied zwischen dem Stichprobenmittelwert und dem Populationsmittelwert zu bewerten.
Der Erwartungswert und die Varianz der t-Verteilung sind wie folgt:
E(t)=0
Der umzuschreibende Inhalt ist: Var(t)=k/(k-1)
Der Grad von Die Freiheit der t-Verteilung (k) stellt die Beziehung zwischen der Stichprobengröße (n) und der Standardabweichung der Grundgesamtheit dar. Wenn k > 30 ist, liegt die t-Verteilung nahe an der Normalverteilung; wenn k nahe bei 1 liegt, wird die t-Verteilung zur Cauchy-Verteilung (Cauchy-Verteilung)
In praktischen Anwendungen, wenn die Stichprobengröße groß ist (n>30) , es kann die Normalverteilung verwenden, um Hypothesentests durchzuführen. In diesem Fall können Sie die Z-Statistik verwenden, um ein Konfidenzintervall festzulegen. Wenn die Stichprobengröße jedoch klein ist (n
Weibull-Verteilung (Weibull-Verteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung.
Die Wahrscheinlichkeitsdichtefunktion der Weibull-Verteilung lautet:
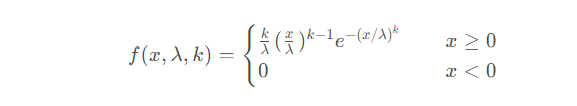
In der Weibull-Verteilung wird x als Zufallsvariable betrachtet, λ wird als Skalenparameter (Skala) bezeichnet und k ist der Formparameter (Form). Was die Weber-Verteilung betrifft, handelt es sich bei k gleich 1 um eine Exponentialverteilung. Wenn λ gleich 1 ist, ist dies die minimierte Weber-Verteilung
Das obige ist der detaillierte Inhalt von11 Grundverteilungen, die Datenwissenschaftler in 95 % der Fälle verwenden. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
